Тема: Производная и ее приложения

По данной теме сначала изучите § 33-42 гл.7 [l]. Затем ознакомьтесь с методическими указаниями по данной теме и внимательно разберите решение примеров из данного пособия. Решите задачи № 2-10, приведенные в пособии.

Производная. Производной функции у = f(x) в точке x называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:

.

Функция, имеющая конечную производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.

Если y= f(u) и и = 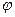(х) - дифференцируемые функции своих аргументов, то производная сложной функции у = f ( 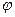(x)) существует и равна произведению производной функции у по промежуточному аргументу и на производную промежуточного аргумента и по независимой переменной х:

Правила дифференцирования

1.	4.
2.	5.
3.

Таблица формул дифференцирования

	8.		15.
	9.		16.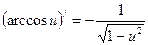
	10.		17.
	11.		18.
	12.		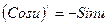19.
	13.		20.
	14.

- элементарные дифференцируемые функции от х, С – (constanta) постоянная величинa.

Пример 1. Найти производную функции

Решение. Дифференцируем функцию по формулам

(u )' = nu u',

Пример 2. Найти производную функции у = sin³ x и вычислить ее значение при

Решение. Это сложная функция с промежуточным аргументом sinx. Дифференцируем ее по формулам (uⁿ)^/ = nu^{n –1} u ^/, (sin u)' = cos и^. и':

Вычислим значение производной при

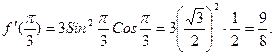
Геометрический смысл производной. Производная функции у = f(x) представляет собой угловой коэффициент касательной, проведенной к графику функции в любой его точке.

Угловой коэффициент касательной, проведенной к графику функции f(х) в точке A(a;b), равен значению производной функции при х = a:

K= y^/ (f)= f ^/ (a)

Уравнение касательной, проведенной к графику функции в этой точке, имеет вид

y-b = k(x-a), где k = f(a) или

Пример 3. Составить уравнение касательной, проведенной к графику функции в точке с абсциссой х = 2.

Решение. Сначала найдем ординату точки касания А(2;у). Так как точка А лежит на кривой, то ее координаты удовлетворяют уравнению кривой, ; А(2; 2).

Уравнение касательной, проведенной к кривой в точке А2;2), имеет вид у-2 = k(x-2). Для нахождения углового коэффициента касательной найдем производную

Угловой коэффициент касательной равен значению производной функ­ции при х = 2:

k = y'(2) =

Уравнение касательной таково: у - 2 = - (х-2), или у-2 = - х + 2, или

х + у - 4 = 0.

Вторая производная. Производной второго порядка (или второй про­изводной)функции называется производная от первой производной у' = f ^/(х): y^// =(y^/)^/ или f ^// = (f ^/ (x))^/.

Пример 4. Найти вторую производную функции f(х) = tgx.

Решение. Сначала по формуле (tgu)' = .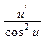

найдем первую производную f ^/ (x) = Дифференцируя еще раз по формулам (u )' = nu u'.

найдем вторую производную:

Приложения производной к исследованию функций. Дифференцируе­мая функция у = f(x) возрастает на промежутке (a; b), если ее производная положительна в каждой точке этого промежутка.

Дифференцируемая функция у = f(x) убывает на промежутке (а;b), если ее производная отрицательна в каждой точке этого промежутка.

Функция у = f(x) имеет максимум в точке x = x₁, если для всех значений х, достаточно близких к x₁ выполняется неравенство f(x)< f(x₁); х = х₁ - точка максимума; у_max =f(x₁) - максимум функции.

Функция у = f(x) имеет минимум в точке x= x₂, если для всех значений х, достаточно близких к x₂, выполняется неравенство f(x)> f(x₂); х = x₂ - точка минимума; y _min= f(x₃) - минимум функции.

Точки максимума и минимума называются точками экстремума, а зна­чения функции в этих точках - экстремальными.

Точки, в которых производная функции обращается в нуль, называются критическими точками 1 рода.

Достаточное условие существования экстремума функции. Если при переходе через критическую точку I рода х=x ₀ производная функции у = f(x) меняет знак, то х = х₀ - точка экстремума.

При этом если производная меняет знак с плюса на минус, то х = х₀ -точка максимума, а у_max = f(x₀). Если же производная меняет знак с минуса на плюс, то х = х₀ - точка минимума, а у_min = f(x₀).

Направление вогнутости и точки перегиба кривой. Говорят, что на про­межутке (а; Ь) кривая обращена выпуклостью вверх или выпукла (), если она лежит ниже касательной, проведенной в любой ее точке.

Говорят, что на промежутке (а;b) кривая обращена выпуклостью вниз или вогнута (), если она лежит выше касательной, проведенной в любой ее точке.

Точка А, в которой меняется направление вогнутости кривой, называет­ся точкой перегиба кривой.

График дифференцируемой функции у = f(x) является выпуклым на промежутке (а;b), если вторая производная функции отрицательна в каждой точке этого промежутка.

График дифференцируемой функции у=f(x) является вогнутым на промежутке (а;b), если вторая производная функции положительна в каждой точке этого промежутка.

Точки, в которых вторая производная функции обращается в нуль, назы­ваются критическими точками II рода.

Если при переходе через критическую точку II рода х=x₀ вторая произ­водная функции меняет знак, то х = х₀ - абсцисса точки перегиба. Ордината точки перегиба равна значению функции в точке x₀; A(x₀; f(x₀)) - точка пере­гиба графика функции у = f(x).

Прямая L называется асимптотой кривой у = f(x), если расстояние точ­ки М(х;у) кривой от прямой L стремится к нулю при неограниченном удале­нии этой точки по кривой от начала координат.

Прямая х = а является вертикальной асимптотой графика функции у = f(x), если

Прямая у = kx+b является наклонной асимптотой графика функции у = f(x), если существуют пределы

Если k = 0, то прямая задается уравнением у = b и называется горизонтальной асимптотой.

Исследование функций и построение их графиков. Исследование функции можно проводить по следующей схеме:

1. Найти область определения функции.

2. Исследовать функцию на четность (нечетность).

3. Исследовать функцию на периодичность.

4. Найти точки пересечения графика функции с осями координат.

5. Найти асимптоты графика функции.

6. Найти промежутки монотонности и экстремумы функции.

7. Найти направление вогнутости и точки перегиба графика функции.

8. Построить график функции.

9. Дополнительные точки графика функции для бесконечно больших по модулю х.

Пример 5. Исследовать функцию у = и построить ее график.

Решение. I. Областью определения функции служит множество всех действительных чисел, за исключением х = ±2, т. е. D(y) = (- ;-2) (- 2;2) (2; ).

2. Функция является нечетной, так как область определения симметрична относительно нуля и f(-x) = .

3. Функция не является периодической.

4.Находим точки пересечения графика функции с осями координат:

с осью Ox: y = 0, то =0 решить это уравнение х=0

с осью Оу: х = 0, у = = 0.

5. Точки разрыва х = ±2, причем lim = ; следовательно, прямые

х = ±2 являются вертикальными асимптотами графика функции.

Найдем наклонную асимптоту:

Наклонная асимптота задается уравнением у = х.

5.Находим промежутки монотонности и экстремумы функции. Для этого сначала найдем производную у' = Затем найдем критические точки I рода: решить уравнение , х₁=0, х₂= , х₃= .. Отметим эти точки в области определения функции. Исследуем знак производной в каждом интервале;

у ^/ (-4)>0, у^/ (-3)<0, У^/ (-1)<0, У^/ (1)<0, У^/ (3)<0, У^/ (4)>0. Функция возрастает при и убывает при ). Итак, х₂= - точка мак­симума; у_max = y()= ,; х = - точка минимума; у_min = у( ) = .

7. Находим направление вогнутости и точки перегиба графика функции. Для этого сначала найдем вторую производную у" = , а затем критические точки II рода: у^// = 0, 8x³ +96x= 0, x= 0. Отметим эту точку в области определения функции т.е. на прямой. Исследуем знак второй производной в каждом интервале: у" (-3)<0, у" (-1)>О, у" (1)<0, у" (3)>0.

Таким образом, график является выпуклым при х и во­гнутым при х (-2;0) (2; ); x = 0 - абсцисса точки перегиба; О(0;0) -точка перегиба графика функции.

8. В системе координат построим прямые, являющиеся асимптотами графика функции, отметим все полученные точки и соединим их плавной кривой.

9. Если точек для построения графика не достаточно, то необходимо взять дополнительно несколько значений х из области определения функции и найти соответствующие значения у.