
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Расчет калибров для контроля деталей гладких цилиндрических сопряжений
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе
по дисциплине « Нормирование точности и технические
измерения»
Выполнил Здоровцова Т.В.
Руководитель Петрусенко П.А.
Минск 2008
СОДЕРЖАНИЕ
СОДЕРЖАНИЕ.. 3
1. Расчет посадок гладких цилиндрических сопряжений. 4
1.1 Расчет посадки с зазорам Ø12Н8/d9. 4
1.2 Расчет переходной посадки Ø160Н7/k6. 7
2. Расчет калибров для контроля деталей гладких цилиндрических сопряжений. 10
3. Выбор средств измерений. 14
4. Выбор, обоснование и расчёт посадок подшипников качения. 18
5. Расчет допусков и посадок шпоночного соединения. 22
6. Выбор и расчёт точностных параметров зубчатых колёс. 25
7. Расчет допусков и посадок резьбовых сопряжений. 28
6.1. Расчет резьбовой посадки M10-4H6H/4jk. 28
6.2. Расчет резьбовая посадки М48х2-7G/7g6g. 29
8. Расчет допусков и посадок шлицевого соединения. 31
Литература. 35
1. Расчет посадок гладких цилиндрических сопряжений.
1.1 Расчет посадки с зазорам Ø12Н8/d9.
Выбор посадки зубчатого колеса на вал определяется условиями работы передачи. Основным назначением распорной втулки является фиксация размера между подшипником качения и зубчатым колесом. Особых требований по точности сопряжения предъявлять нет надобности, соединение должно собираться легко, поэтому для данного соединения назначаем посадку с зазором Ø12Н8/d9.
Рассчитываем предельные размеры отверстия Ø12Н8.
По ГОСТ 25346-89 «Основные нормы взаимозаменяемости. Единая система допусков и посадок. Общие положения, ряды допусков и основных отклонений» определяем значения допуска IT8 = 27 мкм и основного (нижнего) отклонения EI = 0 мкм.
Верхнее отклонение будет равно
ES = EI + IT9 = 0 + 27 = +27 мкм.
Предельные размеры отверстия:
Dmin = D0 + EI = 12,000 + 0 = 12,000 мм;
Dmax =D0 + ES = 12,000 +0,027 = 12,027 мм.
Рассчитываем предельные размеры вала Ø12d9.
По ГОСТ 25346 определяем значения допуска IT9 = 43 мкм и основного (верхнего) отклонения es = -50 мкм.
Нижнее отклонение будет равно
ei = es – IT9 = – 50 – 43 = – 93 мкм.
Предельные размеры вала:
dmin = d0 + ei = 12,000 – 0,093 = 11,007 мм;
dmax = d0 + es = 12,000 – 0,050 = 11,050 мм.
Результаты расчётов оформим в виде таблицы.
Таблица 1
| Размер | IT, мкм | ES (es), мкм | EI (ei), мкм | Dmin (dmin), мм | Dmax (dmax), мм |
| Ø12Н8 | + 27 | 12,000 | 12,027 | ||
| Ø12d9 | – 50 | – 93 | 11,007 | 11,050 |
Расчёт предельных размеров сопряжения
Smax = Dmax – dmin = 12,027 – 11,007 = 1,020 мм;
Smin = Dmin – dmax = 12,000 – 11,050 = 0,050 мм.
Средний зазор
Scp = (Smax + Smin)/2 = (1,020 + 0,050)/2 = 0,535 мм.
Допуск посадки
TS = ITD + ITd = 0,027 + 0,043 = 0,070 мм.
Строим схему расположения полей допусков сопрягаемых деталей и рассчитываем предельные значения зазоров.
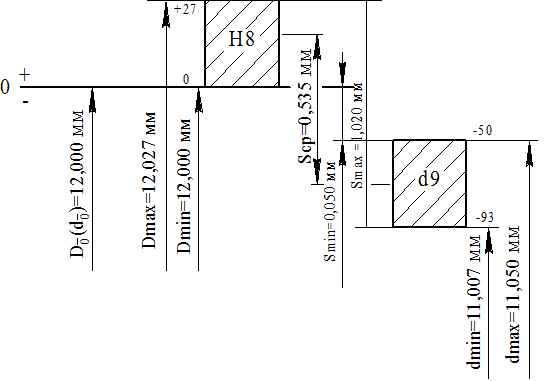
Рис.1.1. Схема расположения полей допусков вала и втулки
Принимаем нормальный закон распределения случайных погрешностей. При распределении размеров в партии деталей по нормальному закону сами зазоры также будут распределены по нормальному закону. Центр группирования зазоров будет соответствовать среднему значению зазора. Таким образом, предельные значения вероятных зазоров можно получить как:
Smax.вер.= Scp + 3sS;
Smin.вер.= Scp – 3sS.
Стандартное отклонение значений нормируемого параметра можно рассчитать по приближенной формуле как шестую часть допуска:
s d = Т d /6,
s D = Т D /6.
Тогда стандартное отклонение посадки получим путем геометрического суммирования стандартных отклонений размеров вала и втулки:
 .
.

Рассчитаем предельные значения вероятных зазоров.
Smax.вер. = 0,535 + 3×0,0846 = 0,7888 мм;
Smin.вер. = 0,535 – 3×0,0846 = 0,2812 мм.
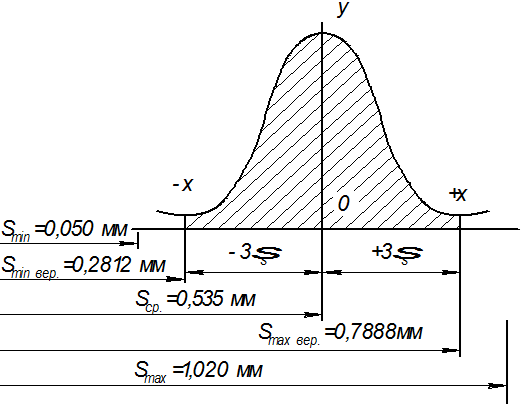
Рис.1.2. Схема распределения вероятных зазоров сопрягаемых деталей
1.2 Расчет переходной посадки Ø160Н7/k6.
Выбор посадки зубчатого колеса на вал определяется условиями работы передачи, точностью передачи, сборкой узла. В нашем случае выбираем переходную посадку Æ160Н7/к6,которая позволит обеспечить точность центрирования сопрягаемых деталей, возможность самоустановки колеса под нагрузкой, легкость сборки и разборки соединения.
Рассчитываем предельные размеры отверстия Ø160Н7.
По ГОСТ 25346-89 «Основные нормы взаимозаменяемости. Единая система допусков и посадок. Общие положения, ряды допусков и основных отклонений» определяем значения допуска IT7 = 40 мкм и основного (нижнего) отклонения EI = 0 мкм.
Верхнее отклонение будет равно
ES = EI + IT9 = 0 + 40 = +40 мкм.
Предельные размеры отверстия:
Dmin = D0 + EI = 160,000 + 0 = 160,000 мм;
Dmax = D0 + ES = 160,000 +0,040 = 160,040 мм.
Рассчитываем предельные размеры вала Ø160k6.
По ГОСТ 25346-89 определяем значения допуска IT6 = 25 мкм и основного (нижнего) отклонения ei = +3 мкм.
Верхнее отклонение будет равно
es = ei + IT6 = +3 + 25 = +28 мкм.
Предельные размеры вала:
dmin = d0 + ei = 160,000 + 0,003 = 160,003 мм;
dmax = d0 + es = 160,000 + 0,028 = 160,028 мм.
Результаты расчётов оформим в виде таблицы.
Таблица 2
| Размер | IT, мкм | ES (es), мкм | EI (ei), мкм | Dmin (dmin), мм | Dmax (dmax), мм |
| Æ160Н7 | + 40 | 160,000 | 160,040 | ||
| Æ160k6 | + 28 | + 3 | 160,003 | 160,028 |
Расчёт предельных размеров деталей сопряжения
Dcp = (Dmax + Dmin)/2 = (160,040 + 160,000)/2 = 160,020 мм;
dcp = (dmax + dmin)/2 = (160,003 + 160,028)/2 = 160,0155 мм;
Smax = Dmax – dmin = 160,040 – 160,003 = 0,037 мм;
Nmax = dmax – Dmin = 160,028 – 160,000 = 0,028 мм;
Допуск посадки
T(S,N) = ITD + ITd = 0,040 + 0,025 = 0,065 мм.
Строим схему расположения полей допусков сопрягаемых деталей и рассчитываем предельные значения табличных зазоров (натягов).

Рис.1.3. Схема расположения полей допусков сопрягаемых деталей
Принимаем нормальный закон распределения размеров и рассчитываем предельные значения вероятных зазоров (натягов). В рассматриваемом сопряжении
Dcp > dcp,
поэтому в данном сопряжении будет большая вероятность возникновения зазоров.
Рассчитываем математическое ожидание и стандартное отклонение зазоров:
MS = Dcp – dcp = 160,020 – 160,0155 = 0,0045 мм;
 .
.
Рассчитаем предельные значения вероятных зазоров и натягов:
Smax.вер. = MS + 3s(S,N) = 0,0045 + 3×0,0079 = 0,0282 мм;
Smin.вер. = MS – 3s(S,N) = 0,0045 – 3×0,0079 = –0,0192 мкм;
Nmax.вер = 19,2 мкм = 0,0192 мм.
При применении переходных посадок в спряжениях возможны зазоры или натяги. Поэтому рассчитываем вероятность их получения. Для определения площади заключенной между кривой Гаусса, осью ординат и осью абсцисс (на чертеже указанная площадь заштрихована) используем табулированные значения функции.
 , где
, где  .
.
В данном случае
х = MS = 4,5 мкм;
s(S,N) = 7,9 мкм.
Тогда
z = MS/ s(S,N) = 4,5/7,9 = 0,57;
Ф(z=0,57) = 0,2156 = 21,56 %
Таким образом, с учетом симметрии распределения, вероятность получения зазоров в сопряжении Æ160Н7/k6 составляет
Р(S) = 50 % + 21,56 % = 71,56 %.
Определим вероятность получения натягов, принимая что 0,9973 ≈ 1
Р(N) = 28,44%.

Рис.1.4. Распределение вероятных зазоров (натягов)
Расчет калибров для контроля деталей гладких цилиндрических сопряжений.
В качестве примера для расчета калибров выбираем гладкое цилиндрическое сопряжение Ø160Н7/k6.
Определяем предельные отклонения и размеры отверстия Ø160Н7.
IT7 = 40 мкм,
ЕI = 0,
ES = +40 мкм;
Dmax = 160,000 + 0,040 = 160,040 мм;
Dmin = 160,000 + 0 = 160,000 мм.
Определяем предельные отклонения и размеры вала Ø160k6.
IT7 = 25 мкм,
ei = +3 мкм,
es = +28 мкм;
dmin = 160,000 + 0,003 = 160,003 мм;
dmax = 160,000 + 0,028 = 160,028 мм.
Строим схемы расположения полей допусков калибров для контроля отверстия и вала:
а) для отверстия Ø160Н7 – схема, приведенная в ГОСТ 24853 (чертеж 1);
б) для вала Ø160k6 – схема, приведенная в ГОСТ 24853 (чертеж 3);
В соответствии с выбранной схемой расположения полей допусков калибров для контроля отверстия Ø160Н7 определяем числовые значения параметров H, Z, Y (таблица 2 ГОСТ 24853).
H = 8 мкм – допуск на изготовление калибров;
Z = 6 мкм – отклонение середины поля допуска на изготовление проходного калибра;
Y = 4 мкм – допустимый выход размера изношенного проходного калибра за границу поля допуска отверстия.
Строим схемы расположения полей допусков калибров для контроля отверстия Ø160Н7 (рис.6).

Рис.2.1. Схема расположения полей допусков калибров
для контроля отверстия Ø 160Н7
Рассчитываем предельные (таблица 1 ГОСТ 24853) и исполнительные размеры калибров для контроля отверстия Ø160Н7, и результаты сводим в таблицу 3.
В соответствии со схемой расположения полей допусков калибров для контроля вала Ø160k6 определяем числовые значения параметров H1, Z1, Y1, Нр (таблица 2 ГОСТ 24853):
H1 = 8 мкм – допуск на изготовление калибров;
Z1 = 6 мкм – отклонение середины поля допуска на изготовление проходного калибра;
Y1 = 4 мкм – допустимый выход размера изношенного проходного калибра за границу поля допуска вала;
Нр = 3,5 мкм – допуск на изготовление контрольного калибра для скобы.
Строим схемы расположения полей допусков калибров для контроля Ø160k6 (рис.41).
Таблица 3
Предельные и исполнительные размеры калибров-пробок
| Обозначение калибра | Размер, мм | |||
| Наибольший | Наименьший | изношенной стороны | исполнительный | |
| ПР | 160,010 | 160,002 | 159,996 | 160,010 - 0,008 |
| НЕ | 160,044 | 160,036 | - | 160,044 - 0,008 |

Рис.2.2. Схема расположения полей допусков калибров
для контроля вала Ø160k6 и контрольных калибров
Рассчитываем предельные (таблица 1 ГОСТ 24853) и исполнительные размеры калибров для контроля вала Ø160k6, и результаты сводим в таблицу 34.
Выполняем эскизы рабочих калибров для контроля отверстия Ø34Н7 (рис.7, а) и вала Ø160k6 (рис. 7, б):
· калибры-пробки – по ГОСТ 14807 – ГОСТ 14826;
· калибры-скобы – по ГОСТ 18358 – ГОСТ 18369.
Таблица 4
Предельные и исполнительные размеры калибров-скоб и контрольных калибров
| Обозначение калибра | Размер, мм | |||
| наибольший | наименьший | изношенной стороны | исполнительный | |
| ПР | 160,026 | 160,018 | 160,032 | 160,018 + 0,008 |
| НЕ | 160,008 | 160,000 | - | 160,000 + 0,008 |
| К-ПР | 160,02325 | 160,02025 | - | 160,02325 - 0,0035 |
| К-НЕ | 160,00475 | 160,00125 | - | 160,00475 - 0,0035 |
| К-И | 160,03325 | 160,03025 | - | 160,03325 - 0,0035 |

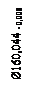

Рис.2.3. Эскизы рабочих калибров:
а) калибр-пробка – для контроля отверстия;
б) калибр-скоба – для контроля вала
Date: 2015-11-14; view: 2797; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |