
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Комплексные числа и действия над ними
Приложение 1
При решении алгебраических уравнений степени два и выше иногда приходится рассматривать конструкции вида  , где
, где 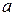 и
и  – некоторые действительные числа. Например, подставляя формально конструкцию
– некоторые действительные числа. Например, подставляя формально конструкцию  в не имеющее действительных корней уравнение
в не имеющее действительных корней уравнение 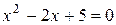 , получаем
, получаем  . Действуя в полученном выражении с конструкцией
. Действуя в полученном выражении с конструкцией  как с двучленом по правилам алгебры, известным из школы, раскрывая скобки и приводя подобные, имеем
как с двучленом по правилам алгебры, известным из школы, раскрывая скобки и приводя подобные, имеем
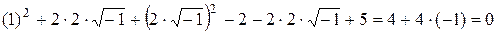 .
.
Таким образом, конструкцию  можно считать корнем новой природы (не действительным) уравнения
можно считать корнем новой природы (не действительным) уравнения 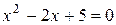 .
.
Пусть  – некоторый формальный символ,
– некоторый формальный символ,  и
и 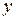 – действительные (вещественные) числа. Конструкции вида
– действительные (вещественные) числа. Конструкции вида  назовём комплексными числами,
назовём комплексными числами,  действительной, а
действительной, а 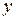 мнимой частями комплексного числа
мнимой частями комплексного числа  и будем обозначать их соответственно
и будем обозначать их соответственно  Два комплексных числа будем считать равными, если совпадают их действительные и мнимые части. На множестве комплексных чисел введём операции сложения и умножения по формулам:
Два комплексных числа будем считать равными, если совпадают их действительные и мнимые части. На множестве комплексных чисел введём операции сложения и умножения по формулам:
 ;
; 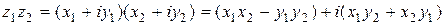 .
.
Обратные операции определяются однозначно и задаются формулами:
 ;
;
 .
.
Каждому комплексному числу  сопоставим точку
сопоставим точку  плоскости
плоскости 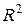 . Этим устанавливается взаимно однозначное соответствие между комплексными числами и точками плоскости. Операция сложения комплексных чисел совпадает с операцией сложения радиус-векторов точек
. Этим устанавливается взаимно однозначное соответствие между комплексными числами и точками плоскости. Операция сложения комплексных чисел совпадает с операцией сложения радиус-векторов точек  . Для операции умножения комплексных чисел не находится соответствующей операции над векторами.
. Для операции умножения комплексных чисел не находится соответствующей операции над векторами.
Если действительные числа отождествить с комплексными числами вида 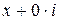 , то эти операции совпадают с обычными операциями над действительными числами и поэтому комплексные числа являются расширением множества действительных чисел. Из введённых выше операций над комплексными числами следует, что для комплексного числа
, то эти операции совпадают с обычными операциями над действительными числами и поэтому комплексные числа являются расширением множества действительных чисел. Из введённых выше операций над комплексными числами следует, что для комплексного числа  получаем
получаем 
Модулем 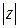 комплексного числа
комплексного числа  назовём длину радиус-вектора точки
назовём длину радиус-вектора точки  , то есть число
, то есть число 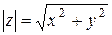 . Тогда
. Тогда
 .
.
Числа 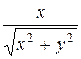 и
и  являются соответственно косинусом и синусом угла
являются соответственно косинусом и синусом угла 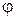 между радиус-вектором точки
между радиус-вектором точки  и осью
и осью 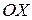 . Поэтому можем записать
. Поэтому можем записать  . Эта форма записи числа
. Эта форма записи числа 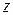 называется тригонометрической формой комплексного числа. Угол
называется тригонометрической формой комплексного числа. Угол 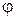 при этом называется аргументом числа
при этом называется аргументом числа 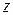 . Совершенно ясно, что числа, аргументы которых отличаются на
. Совершенно ясно, что числа, аргументы которых отличаются на 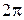 , совпадают. Среди всех значений аргумента числа
, совпадают. Среди всех значений аргумента числа 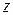 выбирают значение, называемое главным, и обозначают его
выбирают значение, называемое главным, и обозначают его  . Наиболее удобным является выбор главного значения аргумента из промежутков
. Наиболее удобным является выбор главного значения аргумента из промежутков  ,
, 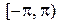 ,
,  . В пакете Mathcad главное значение аргумента выбирается из промежутка
. В пакете Mathcad главное значение аргумента выбирается из промежутка  . При выборе главного значения аргумента из промежутка
. При выборе главного значения аргумента из промежутка  его находят по формулам
его находят по формулам

Формулы для нахождения главного значения аргумента при выборе его из других промежутков предлагается написать самостоятельно. Все значения аргумента обозначают 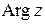 . Отметим, что
. Отметим, что 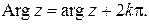
Полагая  , можем записать
, можем записать 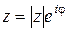 . Эта форма записи числа
. Эта форма записи числа 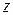 называется показательной формой записи комплексного числа. Так как
называется показательной формой записи комплексного числа. Так как 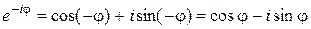 , то, складывая и вычитая с
, то, складывая и вычитая с  , получаем формулы Эйлера:
, получаем формулы Эйлера:
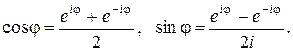
Далее,
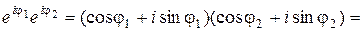
 .
.
Поэтому
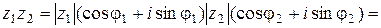
 .
.
Таким образом, мы получили, что при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Аналогично при делении комплексных чисел их модули делятся, а аргументы вычитаются.
Как следствие этих результатов, получаем формулы Муавра:
 ;
;

Пример 1. Найти 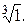
Решение. Так как  то, используя вышеприведённую формулу, имеем
то, используя вышеприведённую формулу, имеем  ,
,  . Придавая
. Придавая 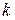 последовательно значения 0,1,2, получаем три значения корня кубического из единицы
последовательно значения 0,1,2, получаем три значения корня кубического из единицы
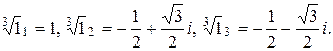
Пример 2. Найти  .
.
Решение. Так как  ,
, 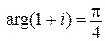 , то
, то  Придавая
Придавая 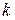 последовательно значения 0,1, получаем два значения
последовательно значения 0,1, получаем два значения  :
:
 ;
; 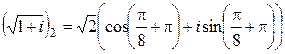 .
.
Заметим, что квадратные корни из комплексных чисел отличаются только знаками.
Пример 3. Решить уравнение  .
.
Решение. Выделяя в левой части полный квадрат, получаем  . Следовательно,
. Следовательно,  . Извлекая квадратный корень из числа
. Извлекая квадратный корень из числа  , имеем
, имеем  . Поэтому
. Поэтому  или
или 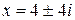 . Подставляя любое из этих комплексных чисел в исходное уравнение, убеждаемся в том, что они являются его решением.
. Подставляя любое из этих комплексных чисел в исходное уравнение, убеждаемся в том, что они являются его решением.
Заметим, что комплексные решения квадратных уравнений могут быть получены по той же формуле, что и действительные, но при отрицательном дискриминанте.
Date: 2015-10-19; view: 429; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |