
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Упражнение 3.3
1 Примените теорему о неявной функции, чтобы показать, что существует единственное решение уравнения
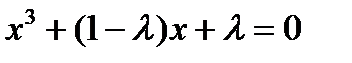
вблизи 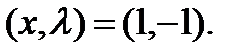
2 Предположим, что плотность населения 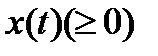 меняется в зависимости от дифференциального уравнения
меняется в зависимости от дифференциального уравнения
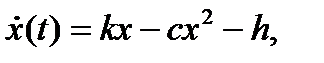
где все коэффициенты 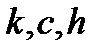 - положительны;
- положительны; 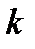 и
и  - мера внутреннего роста населения, и
- мера внутреннего роста населения, и  - скорость уборки урожая. Для положительной исходной плотности населения, население уничтожено, если есть конечное значение
- скорость уборки урожая. Для положительной исходной плотности населения, население уничтожено, если есть конечное значение 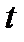 такое, что
такое, что 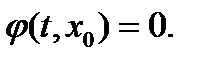
Без нахождения явных решений дифференциального уравнения, показать следующее: (1) Если 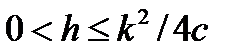 , то тогда существует предельное значение исходного размера населения такое, что если исходный размер население не достигает порогового значения, то население уничтожается. С другой стороны, если исходный размер населения превышает пороговое значение, то население достигает точки равновесия; (2) Если
, то тогда существует предельное значение исходного размера населения такое, что если исходный размер население не достигает порогового значения, то население уничтожается. С другой стороны, если исходный размер населения превышает пороговое значение, то население достигает точки равновесия; (2) Если 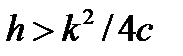 , население уничтожено, независимо от своего первоначального размера.
, население уничтожено, независимо от своего первоначального размера.
3.4 Периодические решения
В этом разделе приведены некоторые примеры существования периодических значений дифференциальных уравнений. Поскольку эта тема сложная, данный раздел только дает некоторые результаты моделирования.
Пример Уравнение Ван-дер-Поля (ВдП).
Уравнение ВдП
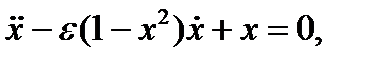 (3.4.1)
(3.4.1)
сыграло важную роль в развитии нелинейной теории, поскольку оно отображает предельные циклы. Параметр 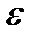 - положителен и мал. Введем
- положителен и мал. Введем 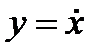 , и уравнение сводится к дифференциальному уравнению первого порядка
, и уравнение сводится к дифференциальному уравнению первого порядка
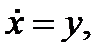
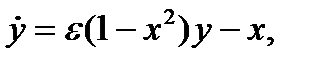 (3.4.2)
(3.4.2)
Как показано на Рисунке 3.4.1, система имеет устойчивый предельный цикл при 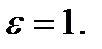
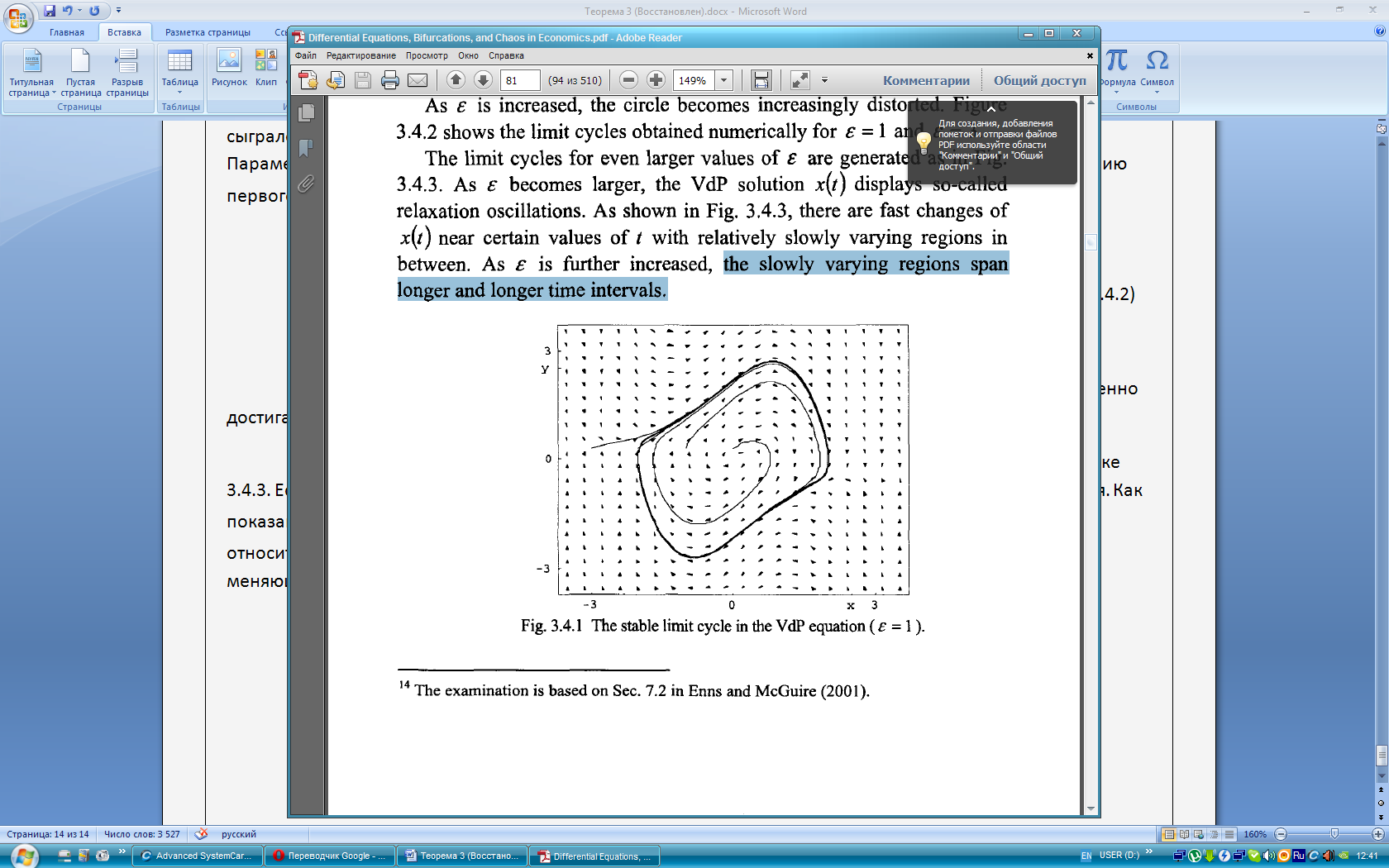
При увеличении 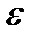 , круг все более искажается. Рисунок 3.4.2 показывает предельный цикл, численно достигающийся при
, круг все более искажается. Рисунок 3.4.2 показывает предельный цикл, численно достигающийся при 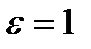 и
и 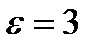 .
.
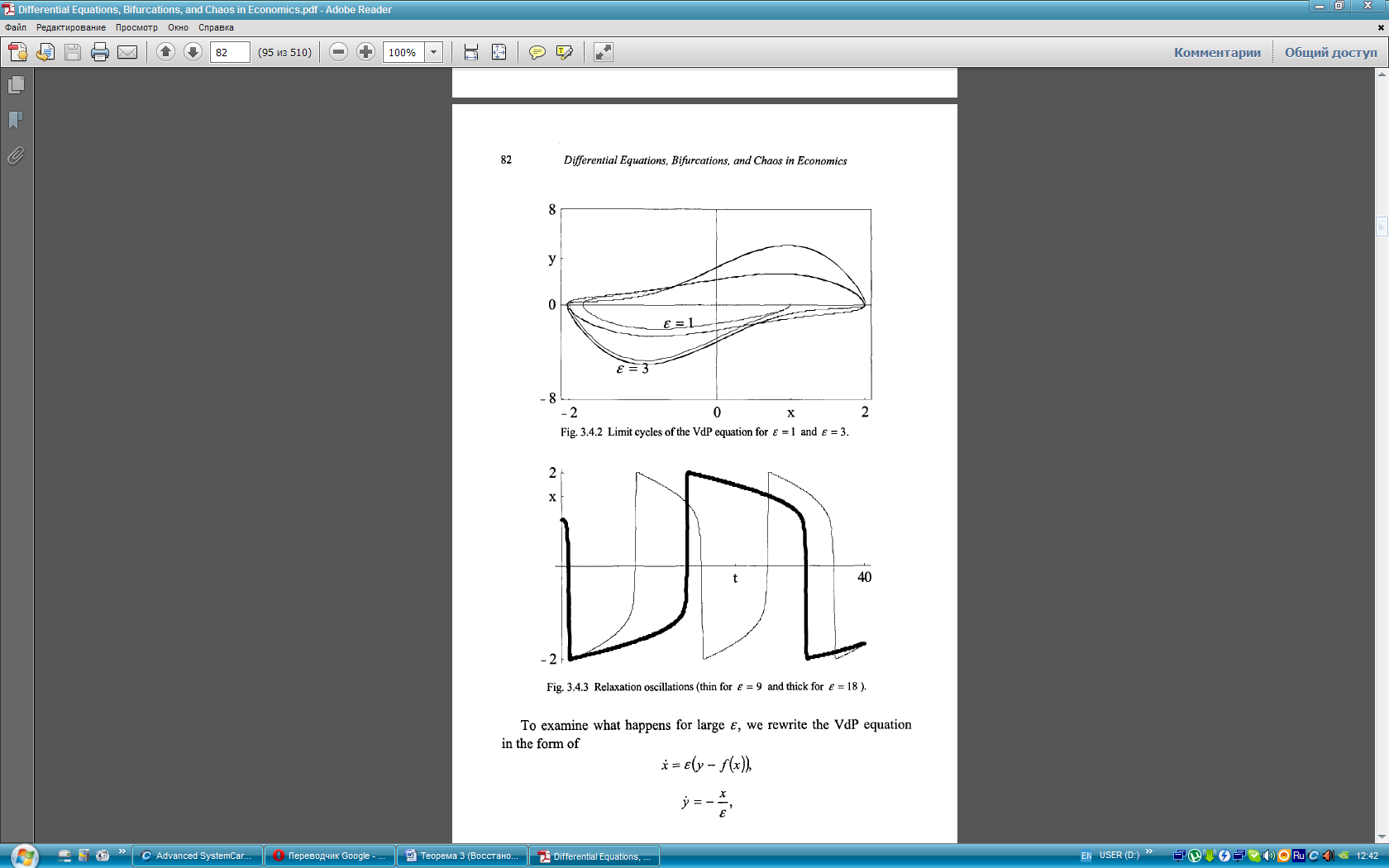
Предельные циклы для каждого еще большего значения 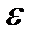 создаются так, как показано на Рисунке 3.4.3. Если
создаются так, как показано на Рисунке 3.4.3. Если 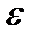 увеличивается, решение
увеличивается, решение 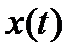 ВдП показывает так называемые релаксационные колебания. Как показано на Рисунке 3.4.3, имеют место быстрые изменение
ВдП показывает так называемые релаксационные колебания. Как показано на Рисунке 3.4.3, имеют место быстрые изменение 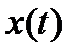 вблизи некоторых значений
вблизи некоторых значений 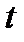 , при относительно медленно меняющейся области между ними. При еще более возрастающем
, при относительно медленно меняющейся области между ними. При еще более возрастающем 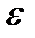 , медленно меняющиеся границы охватывают все большие и большие временные интервалы.
, медленно меняющиеся границы охватывают все большие и большие временные интервалы.
Чтобы исследовать, что происходит при больших 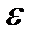 , перепишем уравнение ВдП в форме
, перепишем уравнение ВдП в форме
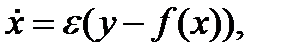
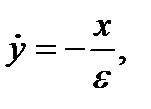
где
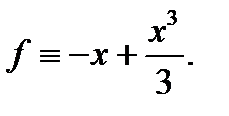
Перепишем верхнее уравнение в форме
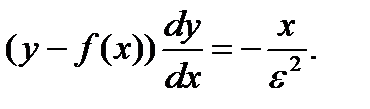 (3.4.3)
(3.4.3)
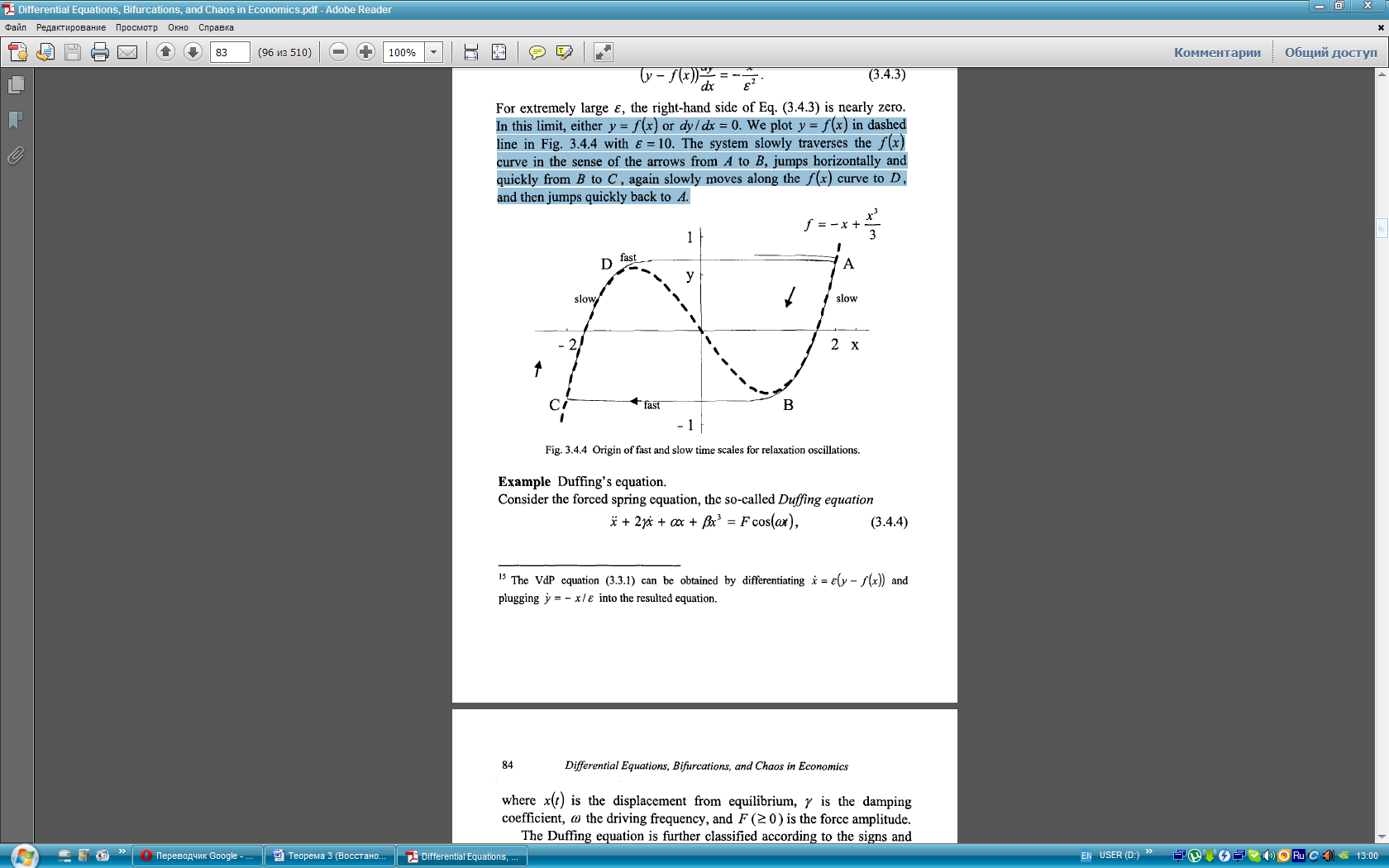
При очень больших 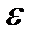 , правая часть Уравнения (3.4.3) практически равна нулю. В этом пределе либо
, правая часть Уравнения (3.4.3) практически равна нулю. В этом пределе либо 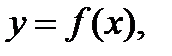 либо
либо 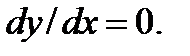 Мы обозначим
Мы обозначим  пунктирной линией на Рисунке 3.4.4 при
пунктирной линией на Рисунке 3.4.4 при 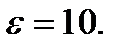 Система медленно пересекает
Система медленно пересекает 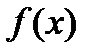 кривой в виде стрелок из А в В, скачки по горизонтали и быстро от В к С, затем снова медленно движется вдоль кривой
кривой в виде стрелок из А в В, скачки по горизонтали и быстро от В к С, затем снова медленно движется вдоль кривой 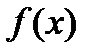 к D, затем опять скачок и быстро возвращается к А.
к D, затем опять скачок и быстро возвращается к А.
Пример Уравнение Дуффинга.
Рассмотрим эластичное уравнение, также имеющее название Уравнение Дуффинга.
 (3.4.4)
(3.4.4)
где 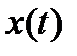 - смещение от равновесия,
- смещение от равновесия, 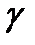 - коэффициент затухания (амортизационный коэффициент),
- коэффициент затухания (амортизационный коэффициент), 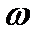 - задающая частота,
- задающая частота, 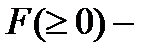 амплитуда силы.
амплитуда силы.
Уравнение Дуффинга классифицируется согласно знакам и значениям параметров 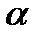 и
и 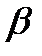 . При
. При 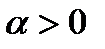 и
и 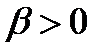 оно известно как жесткий прыжок уравнения Дуффинга (hard spring Duffing equation). Когда
оно известно как жесткий прыжок уравнения Дуффинга (hard spring Duffing equation). Когда 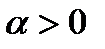 и
и 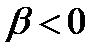 , уравнение имеет название мягкого прыжка уравнения Дуффинга. Две другие важные категории – это негармоничный (
, уравнение имеет название мягкого прыжка уравнения Дуффинга. Две другие важные категории – это негармоничный (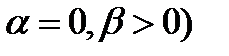 и инвертированный (
и инвертированный (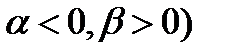 случаи. Введем
случаи. Введем
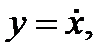
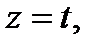
перепишем уравнение Дуффинга с помощью трех одномерных ОДУ (обыкновенное дифференциальное уравнение) с тремя переменными состояниями
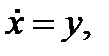
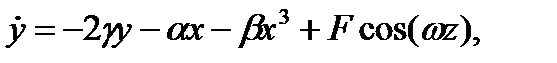

Рисунок 3.4.5 показывает 2 участка поведения уравнения Дуффинга при
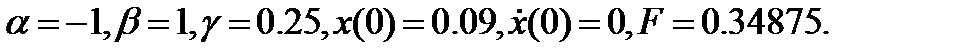
Система показывает 2-периодическое решение как повторение картины каждые два колебания при достижении стационарного положения. Траектория в правой части участка наматывается на замкнутую орбиту, которая пересекает саму себя. В трех изменениях реальные траектории не пересекаются. Эти пересечения являются артефактом в результате того, что мы спроектировали трехмерную фазовую траекторию в двухмерное пространство. Рисунок 3.4.6 показывает хаотичное поведение, когда 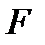 увеличивается до
увеличивается до 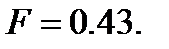 Картина не имеет нерегулярное формы, даже если будет выбран большой временной диапазон.
Картина не имеет нерегулярное формы, даже если будет выбран большой временной диапазон.
3.5 Метод энергетического баланса и периодические решения
Теперь мы введем метод решения уравнения вида
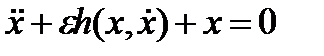 ,
,

где 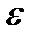 достаточно мало. Такое уравнение близко к уравнению
достаточно мало. Такое уравнение близко к уравнению
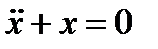 ,
,
чья фазовая диаграмма состоит из окружностей с центром в начале координат. Сейчас мы используем этот факт для построения исходного уравнения.
Рассмотрим
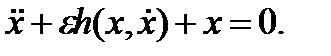 (3.5.1)
(3.5.1)
Уравнение также может быть записано в виде
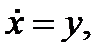
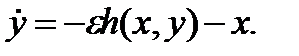 (3.5.2)
(3.5.2)
Предположим, что 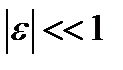 и
и 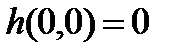 . Точка равновесия находится в точке начала координат. При
. Точка равновесия находится в точке начала координат. При 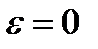 уравнение (3.5.1) принимает вид
уравнение (3.5.1) принимает вид 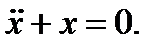 Его общее решение имеет вид
Его общее решение имеет вид
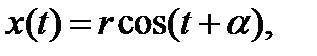
где 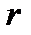 и
и 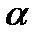 - произвольные константы. Без ограничения общности, мы требуем, чтобы
- произвольные константы. Без ограничения общности, мы требуем, чтобы 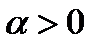 и
и 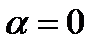 . Семейство фазовых траекторий для
. Семейство фазовых траекторий для 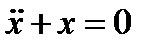 получается из
получается из
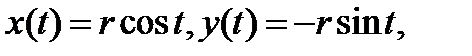 (3.5.3)
(3.5.3)
которые являются семейством окружностей
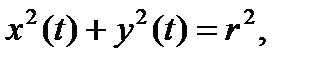
с периодом 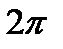 . Введем полную «энергию»
. Введем полную «энергию» 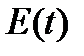 как
как
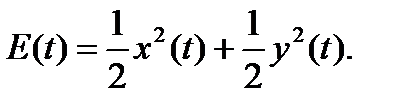
Взяв производные полной энергии и учитывая 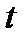 и уравнение (3.5.2), имеем
и уравнение (3.5.2), имеем
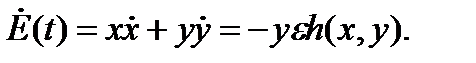
Интегрирование уравнения, указанного выше, от 0 по 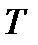 дает
дает
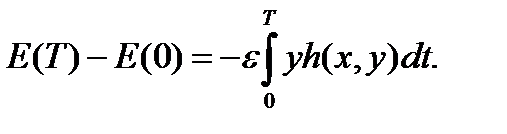
Мы считаем, что чтобы  и
и 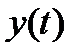 были периодическими,
были периодическими, 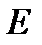 должно вернуться к первоначальному значению после одного цикла. Следовательно, мы должны получить
должно вернуться к первоначальному значению после одного цикла. Следовательно, мы должны получить
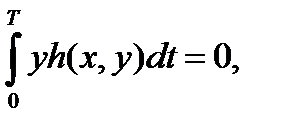 (3.5.4)
(3.5.4)
на предельном цикле. Теперь введем приближение (3.5.3) в уравнение (3.5.4), мы получаем приближенное уравнение
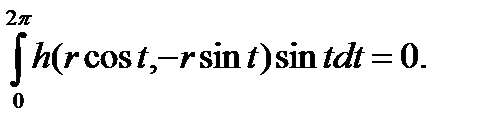 (3.5.5)
(3.5.5)
Решения уравнения (3.5.5) обозначим как 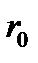 . Кроме того, стабильность цикла тоже может быть определена. Определим функцию
. Кроме того, стабильность цикла тоже может быть определена. Определим функцию 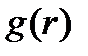
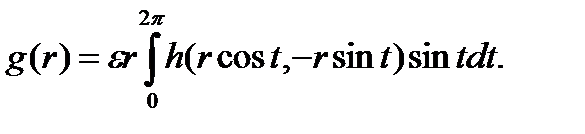
В предельном цикле 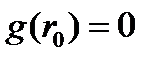 . Условия стабильности таковы, что если
. Условия стабильности таковы, что если 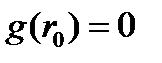 , тогда соответствующий предельный цикл стабилен, если
, тогда соответствующий предельный цикл стабилен, если 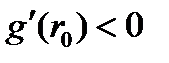 и нестабилен, если
и нестабилен, если  .
.
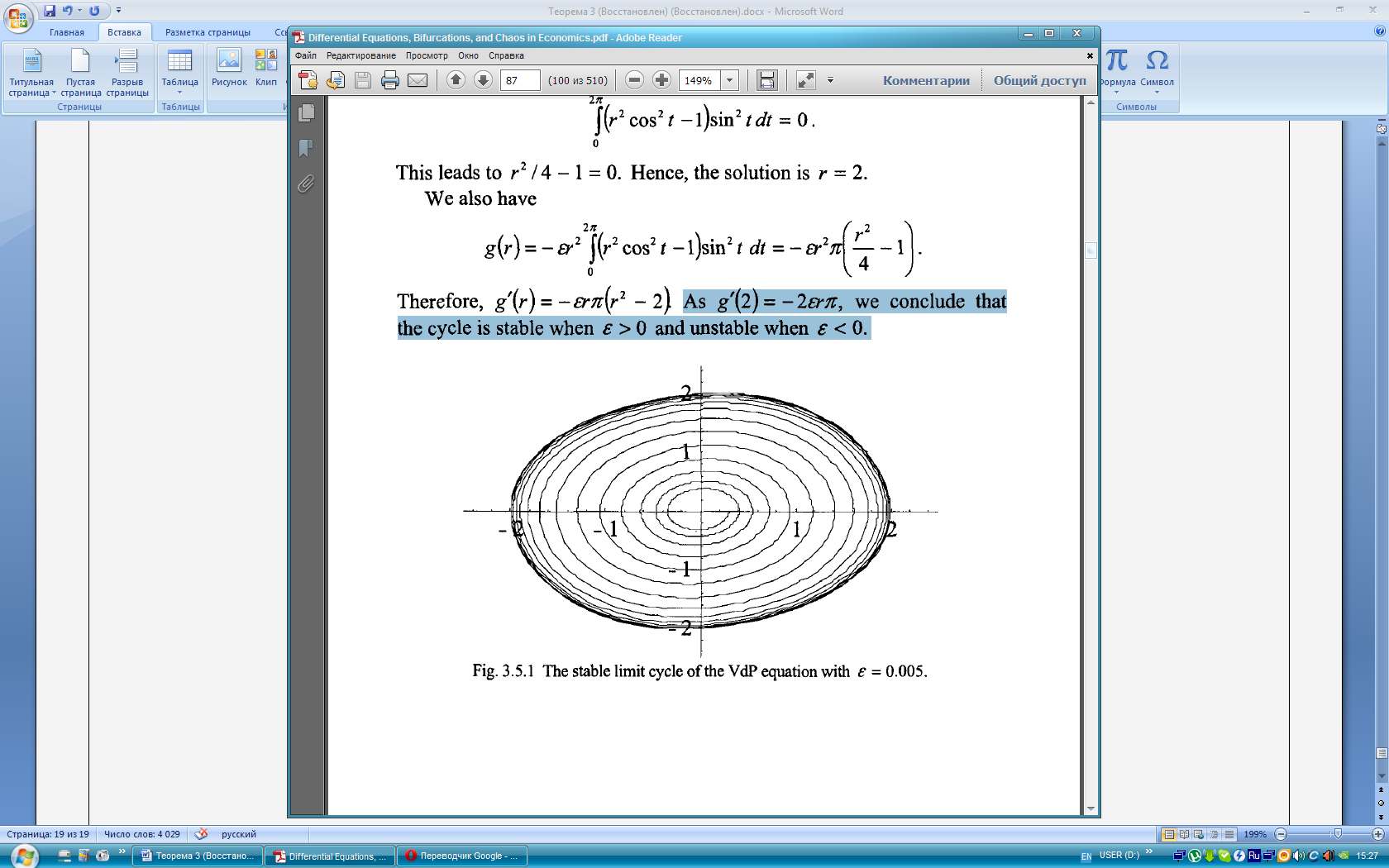
Пример Уравнение ВдП.
В предыдущем разделе было продемонстрировано периодическое поведение уравнения ВдП в случае, когда 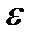 является большим. Когда же
является большим. Когда же  - малое, мы можем аппроксимировать периодическое решение. Сравнив уравнения (3.4.1) и (3.5.1), мы находим
- малое, мы можем аппроксимировать периодическое решение. Сравнив уравнения (3.4.1) и (3.5.1), мы находим
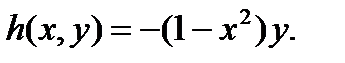
Предполагая, что 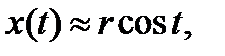 уравнение (3.5.5) принимает вид
уравнение (3.5.5) принимает вид

Это приводит к 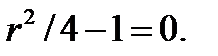 Следовательно, решение -
Следовательно, решение - 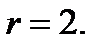
Мы также имеем
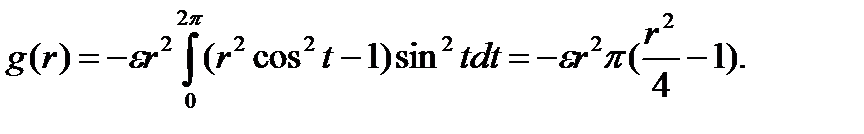
Таким образом, 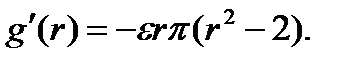 Так как
Так как 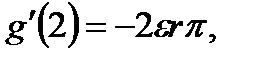 мы заключаем, что цикл стабилен когда
мы заключаем, что цикл стабилен когда 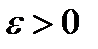 и нестабилен, если
и нестабилен, если 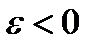 .
.
Упражнение 3.5
1 Применить метод энергетического баланса для нахождения амплитуды и стабильности произвольного предельного цикла каждого из следующих уравнений:
(a) 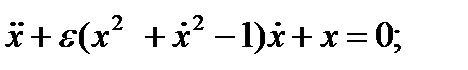
(b) 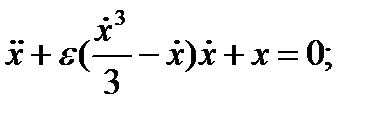
(c) 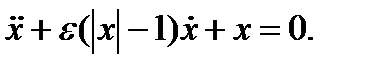
3.6 Оценка амплитуды и частоты
Мы по-прежнему работаем с уравнением (3.5.1)

Уравнение также записано в форме уравнения (3.5.2). Введем полярные координаты
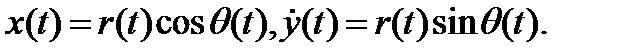
Используя
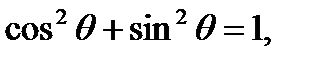
получаем
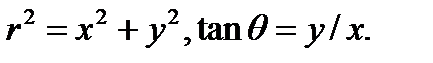
Итак, мы имеем
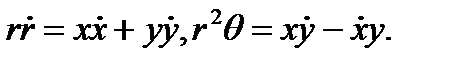
Подставляя уравнение (3.5.2) в уравнения выше, получаем
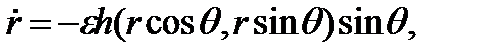
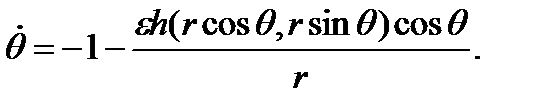 (3.6.1)
(3.6.1)
Дифференциальное уравнение для фазовых траекторий имеет вид
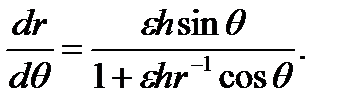 (3.6.2)
(3.6.2)
Предположим, что система содержит предельный цикл или одну из кривых, составляющих центр. Пусть 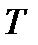 – ее временной период. Тогда
– ее временной период. Тогда 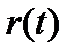 и
и 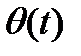 имеют период времени
имеют период времени 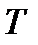 , это означает что
, это означает что 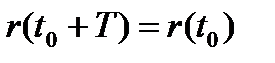 при любых
при любых 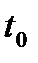 . При очень малых
. При очень малых 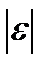 , увеличивающих правую часть уравнения (3.6.2) в силу
, увеличивающих правую часть уравнения (3.6.2) в силу 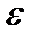 , получаем
, получаем
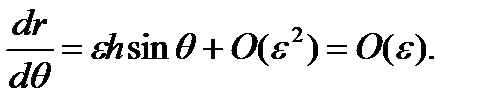 (3.6.3)
(3.6.3)
Интегрируя это уравнение по 2 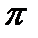 , учитывая
, учитывая 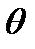 , получаем
, получаем
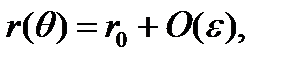
где 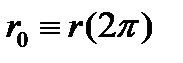 . Интегрируя
. Интегрируя 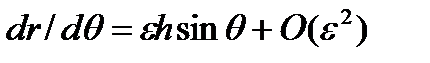 от
от 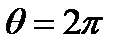 по
по 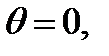 мы имеем
мы имеем

где мы использовали 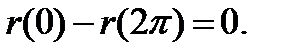 Преобразовав уравнение выше, получаем
Преобразовав уравнение выше, получаем
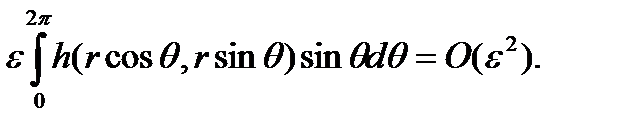
Так как интеграл в левой части не зависит от 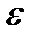 , необходимое условие для фазы пути к замкнутости –
, необходимое условие для фазы пути к замкнутости –
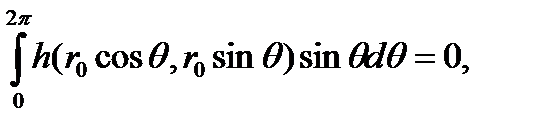 (3.6.4)
(3.6.4)
где мы использовали 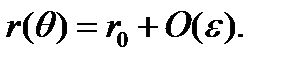 Это уравнение используется для аппроксимации амплитуды
Это уравнение используется для аппроксимации амплитуды 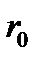 . Интегрируя выражение для
. Интегрируя выражение для  , учитывая
, учитывая 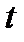 из
из 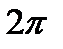 , получается
, получается
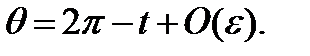
Подставим это в уравнение (3.6.4), чтобы получить
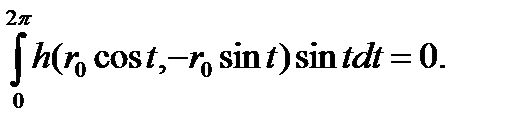 (3.6.5)
(3.6.5)
Из уравнения (3.6.1), период 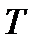 аппроксимируется с помощью
аппроксимируется с помощью
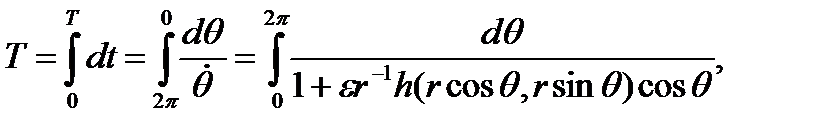 (3.6.6)
(3.6.6)
где мы используем тот факт, что движение для увеличения 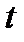 происходит по часовой стрелке, а положительное направление для полярной координаты
происходит по часовой стрелке, а положительное направление для полярной координаты 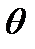 происходит против часовой стрелки. Из
происходит против часовой стрелки. Из  и уравнения (3.6.6) мы получаем
и уравнения (3.6.6) мы получаем 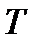 в виде
в виде
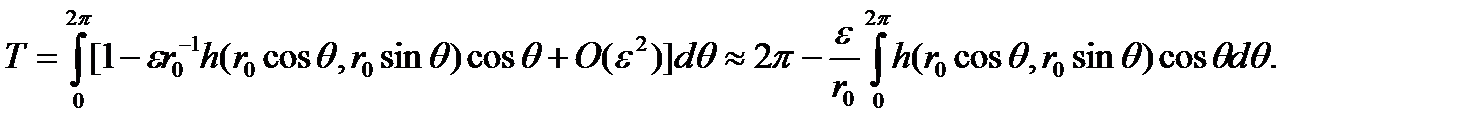
Ошибка имеет порядок  . Круговая частота периодических колебаний
. Круговая частота периодических колебаний
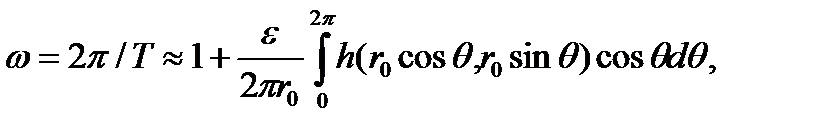 (3.6.7)
(3.6.7)
где 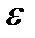 мало. Такое уравнение близко к уравнению
мало. Такое уравнение близко к уравнению
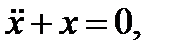
чья фазовая диаграмма состоит из окружностей с центрами в начале координат. Теперь мы используем этот факт для построения приближенного решения исходного уравнения.
Пример Уравнение ВдП
Рассмотрим уравнение (3.4.1). Уравнение (3.6.5) такое же, как уравнение (3.5.5). Амплитуда - 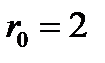 до
до 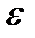 . Из уравнения (3.6.7)
. Из уравнения (3.6.7)
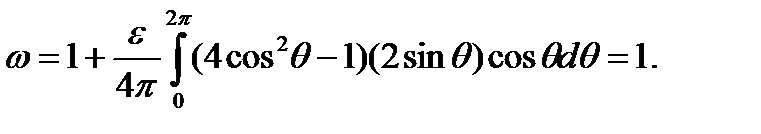
Таким образом, частота – 1 с ошибкой 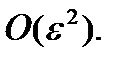
Пример Проанализируем 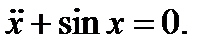 Запишем
Запишем
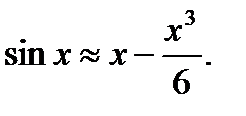
Приближенное уравнение имеет вид
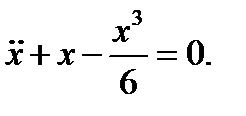
Следовательно, 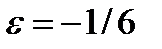 и
и 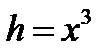 . Уравнение (3.6.5) при амплитуде
. Уравнение (3.6.5) при амплитуде 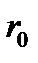 принимает вид
принимает вид
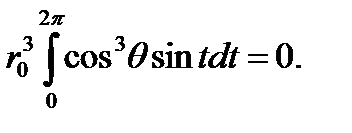
Уравнение выполняется при всех 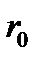 . Уравнение (3.6.7) принимает вид
. Уравнение (3.6.7) принимает вид

Имеем 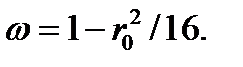
Date: 2015-09-05; view: 304; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |