Тема 1.1 Дифференциальное исчисление

Лекция №1.

План:

1. Производная функции, её геометрический и механический смысл. Формулы производных.

2. Изучение производных суммы, произведения, частного функций. Обоснование производных элементарных и сложных функций, обратных функций.

Определение 1: Производная есть скорость изменения функции в окрестности данной точки.

Пусть дана некоторая функция у = у(х). Ее производная определяется следующим образом:

Определение 2: Дифференциалом функции (аргумента) называется бесконечно малое приращение функции (аргумента).

Для той же самой функции у = у(х) дифференциалы имеют следующее обозначения: dx – дифференциал аргумента, dy – дифференциал функции.

		(2)

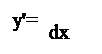dy = y´ dx

- производная есть отношение дифференциала функции к дифференциалу аргумента.

Определим ГЕОМЕТРИЧЕСКИЙ СМЫСЛ производной и дифференциала. Для этого изобразим фрагмент графика некоторой довольно гладкой функции у = у(х) (рисунок 1).

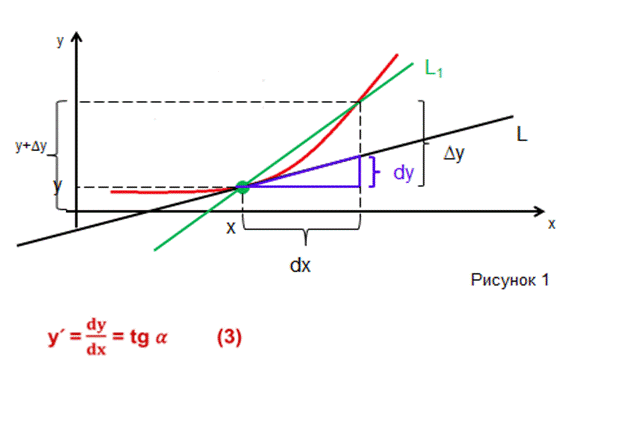
Выделим произвольную точку (х;у) на графике и построим касательную L в этой точке.

Зададимся малым приращением аргумента dx, которое, для наглядности. Изобразим покрупнее.

Определим соответствующее приращение функции ∆у и построим хорду L₁.

Видим, что при dx → 0 эта хорда, вращаясь вокруг точки (х;у), переходит в касательную L.

Таким образом, при бесконечно малом приращении dx хорда L₁ и касательная L НЕРАЗЛИЧИМЫ.

Отметим, что касательная L, совместно с координатными линиями, изображенными на рисунке, образует прямоугольный треугольник. Горизонтальный катет равен dx, вертикальный катет обозначим через dy.

Видим, что при dx → 0 величина dy практически совпадает с приращением функции, ∆у → dy. То есть dy – это ДИФФЕРЕНЦИАЛ функции. Следовательно, учитывая (2), получаем

		(3)

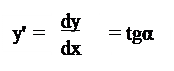- производная функции равна тангенсу угла между касательной к графику функции в данной точке и осью Ох.

Напомним, что операция вычисления производной называется дифференцированием.

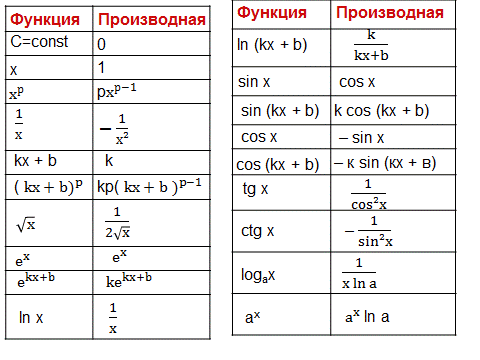
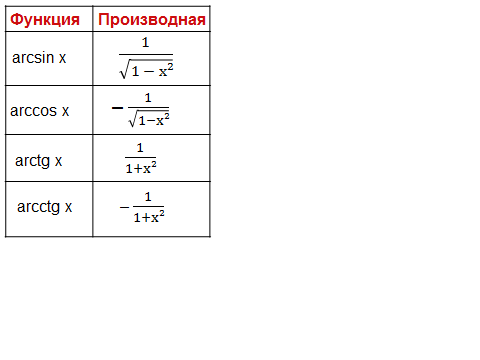
Таблица производных.