
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры линейных операторов
Линейный оператор и его матрица.
Определение линейного оператора.
Определение 1. Отображение A из пространства  в пространство
в пространство 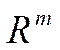 называется линейным отображением, или линейным оператором, если для любых векторов
называется линейным отображением, или линейным оператором, если для любых векторов 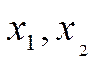 из
из 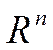 и любой константы
и любой константы  выполняются равенства:
выполняются равенства:
1° 
2° 
Эти два равенства эквивалентны одному:
3) 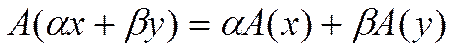
Заметим, что линейный оператор всегда отображает нулевой вектор в нулевой вектор. По свойству линейности,  .
.
Там, где это не сможет привести к недоразумениям, вместо А (х) мы будем писать Ах.
ПРИМЕРЫ ЛИНЕЙНЫХ ОПЕРАТОРОВ
1. Тождественный оператор – оператор, который отображает пространство 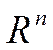 в себя и каждому x Î
в себя и каждому x Î  ставит в соответствие его самого называется тождественным оператором и обозначается E: Ex = x " x Î
ставит в соответствие его самого называется тождественным оператором и обозначается E: Ex = x " x Î  .
.
2. 
 Оператор, который каждому x Î
Оператор, который каждому x Î 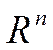 ставит в соответствие нуль-вектор 0 из
ставит в соответствие нуль-вектор 0 из 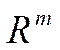 , называется нулевым оператором.
, называется нулевым оператором.
3. Оператор Px проектирования на ось x ставит в соответствие любому вектору на плоскости a его геометрическую проекцию a x на ось x.
4. Оператор поворота Wj на угол j вектору на плоскости a ставит в соответствие вектор, который получается из a поворотом в положительном направлении (против часовой стрелки) на угол j. Условия 1° и 2° проверяются без труда. Проверим, например, условие 1°.  означает, что векторы
означает, что векторы 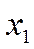 и х2 сначала складываются, а затем полученный вектор поворачивается.
и х2 сначала складываются, а затем полученный вектор поворачивается.  означает, что векторы х1 и х2 сперва поворачиваются, а затем складываются. Ясно, что в обоих случаях результат один и тот же.
означает, что векторы х1 и х2 сперва поворачиваются, а затем складываются. Ясно, что в обоих случаях результат один и тот же.
 5. Оператор S покоординатного сдвига в R 3 ставит в соответствие вектору a Î R 3 вектор Sa Î R 3 по следующему правилу:
5. Оператор S покоординатного сдвига в R 3 ставит в соответствие вектору a Î R 3 вектор Sa Î R 3 по следующему правилу:  т. е. i-я координата получает значение (i - 1)-й координаты, а первая координата заменяется нулем.
т. е. i-я координата получает значение (i - 1)-й координаты, а первая координата заменяется нулем.
6. Рассмотрим произвольную  -матрицу А.
-матрицу А.
А = 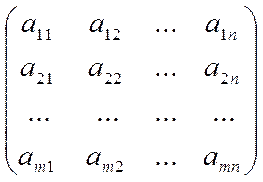
Совокупность равенств
 Или в компактной форме записи
Или в компактной форме записи  определяет линейный оператор, действующий из
определяет линейный оператор, действующий из  в
в 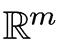 . В самом деле,
. В самом деле,  и
и 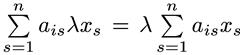 . Как мы вскоре увидим, этот пример является в определенном смысле универсальным.
. Как мы вскоре увидим, этот пример является в определенном смысле универсальным.
1.3.Связь между координатами образа и прообраза при линейном отображении.Матрица линейного оператора.
Пусть A линейный оператор действующий из пространства 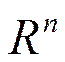 в пространство
в пространство  .Зафиксируем в каждом из пространств базисы:
.Зафиксируем в каждом из пространств базисы: 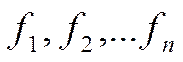 -базис в
-базис в 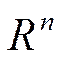 ,
, 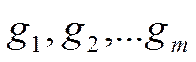 -базис в
-базис в 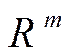 .Возьмем произвольный вектор x из
.Возьмем произвольный вектор x из  и разложим его по базису:
и разложим его по базису:  или в компактной форме записи с использованием знака суммы
или в компактной форме записи с использованием знака суммы  .Подействуем на него оператором A, получим Ax=y. Разложим y по базису y=
.Подействуем на него оператором A, получим Ax=y. Разложим y по базису y= 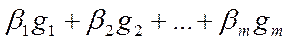 или
или
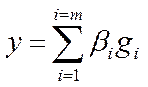 C другой стороны в силу линейности оператора A
C другой стороны в силу линейности оператора A
y=Ax=A( )=
)= 
Каждый из векторов  разложим по базису пространства
разложим по базису пространства  , получим
, получим

Подставляя все это в разложение y, будем иметь
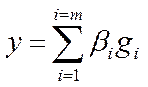
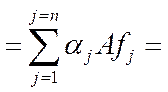

Сравнивая левую и правую части, в силу единственности разложения по базису, получим
 i=1,2,…m (1) или подробнее
i=1,2,…m (1) или подробнее
 , (1)
, (1)
Формулы(1) устанавливают связь между координатами образа у и координатами прообраза х при линейном отображении A. Матрицу коэффициентов в формулах (1)
А = 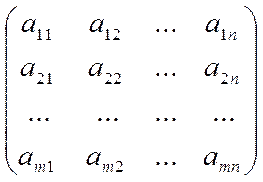
назовем матрицей линейного оператора A в выбранных базисах f,g. Из формул(1) следует, что матрица линейного оператора действующего из пространства 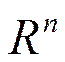 в пространство
в пространство  имеет размерность
имеет размерность
mхn и в фиксированных базисах f,g строится следующим образом: в k-том k=1,2, …n столбце матрицы А находятся координаты вектора 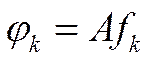 в базисе
в базисе 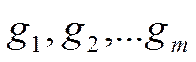 .
.
Замечание. Мы установили, что при выбранных базисах 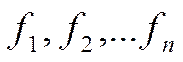 и
и 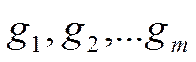 каждому линейному оператору соответствует
каждому линейному оператору соответствует 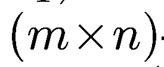 -матрица, столбцами которой являются координаты векторов
-матрица, столбцами которой являются координаты векторов 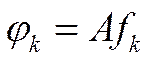 . Ранее (см. пример 6) было установлено, что каждой
. Ранее (см. пример 6) было установлено, что каждой 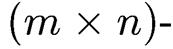 матрице
матрице
соответствует линейный оператор, определяемый формулой (1). Таким образом, при выбранных базисах 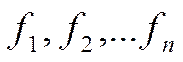 и
и 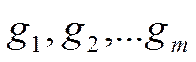 соответствие между линейными операторами и
соответствие между линейными операторами и  -матрицами является взаимно
-матрицами является взаимно
однозначным.
Примеры.
1.Матрица тождественного оператора.
Возьмем в 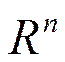 два одинаковых произвольных базиса. Тождественный оператор действует по правилу
два одинаковых произвольных базиса. Тождественный оператор действует по правилу  Следовательно, мы получим квадратную матрицу размера nxn, все элементы которой кроме диагональных равны нулю, а диагональные элементы равны 1.Эту матрицу
Следовательно, мы получим квадратную матрицу размера nxn, все элементы которой кроме диагональных равны нулю, а диагональные элементы равны 1.Эту матрицу 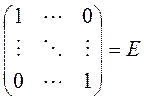 принято называть единичной.
принято называть единичной.
2.Матрица нулевого оператора.
Зафиксируем в каждом из пространств базисы: 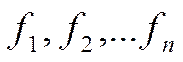 -базис в
-базис в 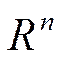 ,
, 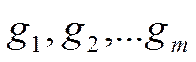 -базис в
-базис в 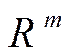 .Так как нулевой оператор Q действует по правилу
.Так как нулевой оператор Q действует по правилу
 ,
,
то мы получим прямоугольную матрицу размера mxn, все элементы которой равны нулю
3. Матрица оператора Px проектирования на ось x.
Возьмем на плоскости базис 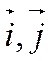 и на оси ох базис
и на оси ох базис  .Так как мы
.Так как мы
Px  =
=  =1
=1  , Px j=0 i, мы получим матрицу размера 1x2 Px. =(1 0).
, Px j=0 i, мы получим матрицу размера 1x2 Px. =(1 0).
4.Матрица оператора поворота Wj.
 Возьмем на плоскости декартовы базисы
Возьмем на плоскости декартовы базисы 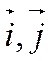 .Тогда
.Тогда
как видно из рисунка Wj  =Соs
=Соs 
 +Sin
+Sin  j, Wj
j, Wj 
Оператор поворота Wj на угол j имеет в стандартном на плоскости матрицу 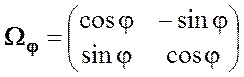 ..
..
5.Матрица оператора S покоординатного сдвига в R 3.
Берем декартовы базисы  ,действуем на каждый из них оператором S:S
,действуем на каждый из них оператором S:S 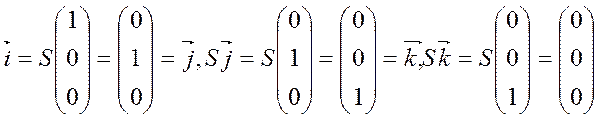
В стандартном базисе имеет матриц S имеет вид:
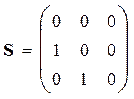 .
.
6.Ясно почему этот пример в начале параграфа был назван универсальным: мы задали линейный оператор матрицей.А
сейчас мы видим что матрицей можно задать любой линейный оператор.
7.Пусть А  матрица оператора А в фиксированных базисах:
матрица оператора А в фиксированных базисах: 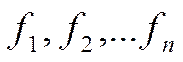 -базис в
-базис в 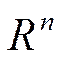 ,
, 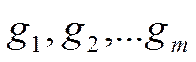 -базис в
-базис в 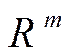 .Найти матрицу этого оператора в базисах 1.
.Найти матрицу этого оператора в базисах 1. 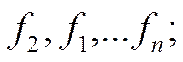
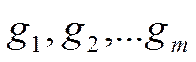 ;
;
2. 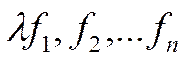 ;
; 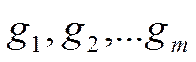 ;
;
3. 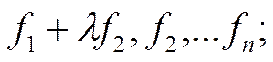
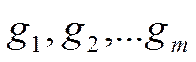 .
.
Решение.1.Пусть А  -матрица оператора А в базисах задачи1;в первом столбце ее будут стоять координаты вектора Af
-матрица оператора А в базисах задачи1;в первом столбце ее будут стоять координаты вектора Af  в базисе
в базисе
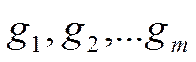 т.е. элементы второго столбца А;во втором столбце ее будут стоять координаты вектора Af
т.е. элементы второго столбца А;во втором столбце ее будут стоять координаты вектора Af  базисе
базисе
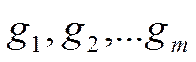 т.е. элементы первого столбца А;в остальных столбцах А
т.е. элементы первого столбца А;в остальных столбцах А  будут те же элементы что и в матрице А.Таким образом: при перестановке местами базисных векторов
будут те же элементы что и в матрице А.Таким образом: при перестановке местами базисных векторов 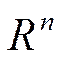 соответствующие столбцы исходной матрицы меняются местами.
соответствующие столбцы исходной матрицы меняются местами.
2. Пусть А  -матрица оператора А в базисах задачи2;в первом столбце ее будут стоять координаты вектора A(
-матрица оператора А в базисах задачи2;в первом столбце ее будут стоять координаты вектора A( в базисе
в базисе
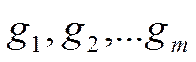 .,но A(
.,но A( =
=  A(
A( .Таким образом: при умножении базисного вектора
.Таким образом: при умножении базисного вектора 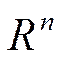 на
на  все коэффициенты соответствующего столбца матрицы оператора А умножаются на
все коэффициенты соответствующего столбца матрицы оператора А умножаются на  .
.
3. Пусть А 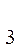 -матрица оператора А в базисах задачи3;в первом столбце ее будут стоять координаты вектора A(
-матрица оператора А в базисах задачи3;в первом столбце ее будут стоять координаты вектора A( в базисе
в базисе 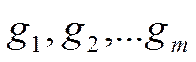 .,но A(
.,но A( =А (
=А ( Таким образом: при прибавлении к базисному вектору
Таким образом: при прибавлении к базисному вектору 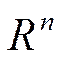 другого базисного вектора, умноженного на
другого базисного вектора, умноженного на  приводит к прибавлению к соответствующему столбцу другого столбца матрицы, умноженного на число
приводит к прибавлению к соответствующему столбцу другого столбца матрицы, умноженного на число  .
.
Общий вывод задачи: при переходе от одного базиса к другому элементарному преобразованию базисных векторов 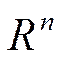 соответствует аналогичное элементарное преобразование над столбцами матрицы оператора в новом базисе.
соответствует аналогичное элементарное преобразование над столбцами матрицы оператора в новом базисе.
7.Исследовать, что происходит с матрицей оператора А 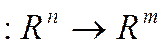 при совершении элементарных преобразований
при совершении элементарных преобразований
с базисом в 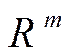 .
.
Решение.1.Пусть 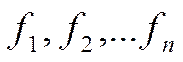 -базис в
-базис в 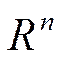 ,
, 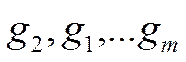 -базис в
-базис в 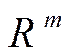 .Найти матрицу оператора А в этих базисах. В h-том столбце h=1,2,…n новой матрицы,будут
.Найти матрицу оператора А в этих базисах. В h-том столбце h=1,2,…n новой матрицы,будут
стоять кооэффициенты разложения вектора A 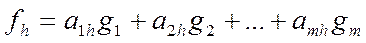 как координаты вектора A
как координаты вектора A  в
в
базисе 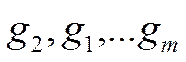 .В новой матрице первая и вторая строчка матрицы А поменяются местами. Таким образом: при перестановке местами. базисных векторов
.В новой матрице первая и вторая строчка матрицы А поменяются местами. Таким образом: при перестановке местами. базисных векторов 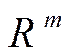 соответствующие строки исходной матрицы А меняются местами.
соответствующие строки исходной матрицы А меняются местами.
2. Пусть 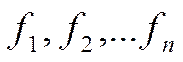 -базис в
-базис в 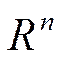 ,
,  -базис в
-базис в 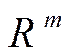 .Найти матрицу оператора А в этих базисах. В h-том столбце h=1,2,…n новой матрицы,будут стоять кооэффициенты разложения вектора А
.Найти матрицу оператора А в этих базисах. В h-том столбце h=1,2,…n новой матрицы,будут стоять кооэффициенты разложения вектора А  как координаты вектора A
как координаты вектора A  в базисе
в базисе  .
.
А 
В новой матрице все элементы первой строки умножатся на 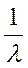 .
.
Таким образом: при умножении базисного вектора 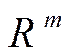 на
на  все коэффициенты соответствующей строки матрицы оператора А умножаются на
все коэффициенты соответствующей строки матрицы оператора А умножаются на 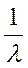 .
.
3. Пусть 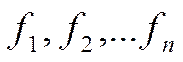 -базис в
-базис в 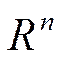 ,
,  -базис в
-базис в 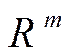 .Найти матрицу оператора А в этих базисах. В h-том столбце h=1,2,…n новой матрицы,будут стоять кооэффициенты разложения вектора А
.Найти матрицу оператора А в этих базисах. В h-том столбце h=1,2,…n новой матрицы,будут стоять кооэффициенты разложения вектора А 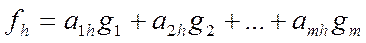 как координаты вектора A
как координаты вектора A  в базисе
в базисе  :
: 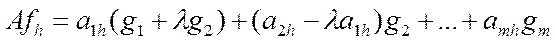
В новом базисе ко второй строке матрицы А прибавляется первая умноженная на (-  ).
).
Общий вывод задачи: при переходе от одного базиса к другому элементарному преобразованию базисных векторов 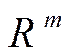 соответствует элементарное преобразование над строками матрицы оператора А в новом базисе.
соответствует элементарное преобразование над строками матрицы оператора А в новом базисе.
| <== предыдущая | | | следующая ==> |
| Б). Створення ЕОМ | | | Task 1. Read and discuss the following lead-in |
Date: 2015-09-02; view: 840; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |