
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства обратной матрицы
· 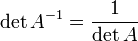 , где
, где 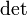 обозначает определитель.
обозначает определитель.
· 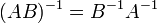 для любых двух обратимых матриц
для любых двух обратимых матриц 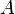 и
и 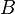 .
.
· 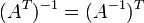 где
где 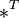 обозначает транспонированную матрицу.
обозначает транспонированную матрицу.
· 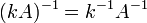 для любого коэффициента
для любого коэффициента 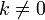 .
.
· Если необходимо решить систему линейных уравнений 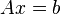 , (b — ненулевой вектор) где
, (b — ненулевой вектор) где 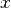 — искомый вектор, и если
— искомый вектор, и если 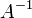 существует, то
существует, то 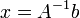 . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе
ТЕОРЕМА о существовании обратной матрицы. Для того, чтобы квадратная матрица А имела обратную матрицу, необходимо и достаточно (<=>), чтобы матрица А была невыражденной — detA<>0;
1. необходимые условия. Дано: А, А -1; Док-ть: detA ¹ 0; Док-во: Предположим detA=0; AA -1 =E; |AA - 1 | = |A| |A -1 | = |E| = 1; |AA - 1 | =0; Противоречие, значит |A| ¹ 0;
2. достаточные условия: Дано A, detA ¹ 0; Док-ть: A -1 -?; Док-во: AA -1 =E -?;
A(a11, a12…a32, A33); Заменим каждый элемент алгебраическим дополнением. В = (A11, A12…A32, A33)*1/|A|; Транспонируем и разделим все элементы на Δ: B T = (A11/Δ, A21/Δ…A23/Δ, A33/Δ); B T =A -1 -?; B T A=E -?
(a11 a12…a32 a33)*(A11A12…A32 A33)=(a11A11+a12A12+a13A13/Δ)=(1 0..0 1)=E;
a21A11+a22A12+a23A13 = 0; a11A11+a12A12+a13A13=Δ;
Алгоритм нахождения. Рассмотрим квадратную матрицу 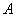 . Обратную матрицу
. Обратную матрицу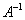 можно найти по следующей формуле:
можно найти по следующей формуле:
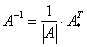 , где
, где 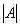 – определитель матрицы
– определитель матрицы 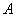 ,
, 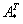 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 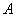 .
.
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Обозначения: Как Вы уже, наверное, заметили, обратная матрица обозначается надстрочным индексом 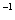
Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.
5. Рангом системы строк (столбцов) матрицы 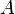 с
с 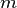 строк и
строк и 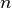 столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Обычно ранг матрицы 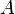 обозначается
обозначается 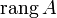 (
(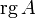 ) или
) или 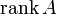 . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
. Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.
Элементарными преобразованиями строк называют:
· перестановка местами любых двух строк матрицы;
· умножение любой строки матрицы на константу 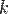 ,
, 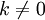 ;
;
· прибавление к любой строке матрицы другой строки.
В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того, что перестановку местами любых двух строк матрицы можно получить, используя умножение любой строки матрицы на константу 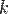 ,
, 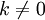 и прибавление к любой строке матрицы другой строки, умноженной на константу
и прибавление к любой строке матрицы другой строки, умноженной на константу 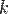 ,
, 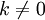 .
.
Аналогично определяются элементарные преобразования столбцов.
Элементарные преобразования обратимы.
Обозначение 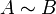 указывает на то, что матрица
указывает на то, что матрица 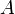 может быть получена из
может быть получена из 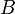 путём элементарных преобразований (или наоборот).
путём элементарных преобразований (или наоборот).
Рангом системы строк (столбцов) матрицы 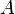 с
с 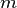 строк и
строк и 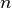 столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Ранг матрицы — Размерность образа 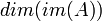 линейного оператора, которому соответствует матрица.
линейного оператора, которому соответствует матрица.
Обычно ранг матрицы 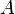 обозначается
обозначается 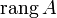 (
(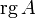 ) или
) или 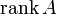 . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
. Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
Определение
Пусть 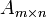 — прямоугольная матрица.
— прямоугольная матрица.
Тогда по определению рангом матрицы 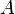 является:
является:
· нуль, если 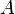 — нулевая матрица;
— нулевая матрица;
· число 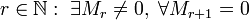 , где
, где 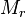 — минор матрицы
— минор матрицы 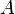 порядка
порядка  , а
, а 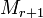 — окаймляющий к нему минор порядка
— окаймляющий к нему минор порядка 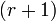 , если они существуют.
, если они существуют.
Теорема (о корректности определения рангов). Пусть все миноры матрицы 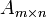 порядка порядка 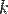 равны нулю ( равны нулю ( ). Тогда ). Тогда 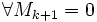 , если они существуют. , если они существуют.
|
6. Линейная зависимость.Если линейная комбинация 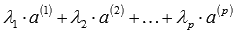 может представлять собой нулевой вектор тогда, когда среди чисел
может представлять собой нулевой вектор тогда, когда среди чисел 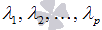 есть хотя бы одно, отличное от нуля, то система векторов
есть хотя бы одно, отличное от нуля, то система векторов 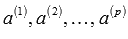 называется линейно зависимой.
называется линейно зависимой.
Если линейная комбинация 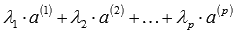 представляет собой нулевой вектор только тогда, когда все числа
представляет собой нулевой вектор только тогда, когда все числа 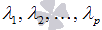 равны нулю, то система векторов
равны нулю, то система векторов 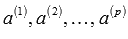 называется линейно независимой.
называется линейно независимой.
Столбцы матрицы — это линейные комбинации столбцов матрицы с коэффициентами, взятыми из матрицы; строки матрицы — это линейные комбинации строк матрицы с коэффициентами, взятыми из матрицы.
Теорема о ранге матрицы. Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А). Доказательство. Пусть 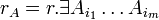 - столбцы, не входящие в БМ и они - максимальная линейно независимая система. ранг системы столбцов
- столбцы, не входящие в БМ и они - максимальная линейно независимая система. ранг системы столбцов 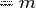 (число столбцов входящих в максимальную линейно независимую систему)
(число столбцов входящих в максимальную линейно независимую систему) 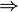 по утверждению 1 (если система линейно независима (количество
по утверждению 1 (если система линейно независима (количество 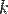 ) и выражается через другую (количество
) и выражается через другую (количество 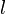 ) то
) то 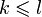 )
) 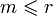 . по утверждению 1 и утверждению 2 (все максимальные линейно независимые системы состоят из одного и тогоже числа столбцов) и в силу того, что все столбцы линейно выражаются через столбцы максимальной линейно независимой системы
. по утверждению 1 и утверждению 2 (все максимальные линейно независимые системы состоят из одного и тогоже числа столбцов) и в силу того, что все столбцы линейно выражаются через столбцы максимальной линейно независимой системы 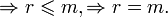
7.Системой m линейных уравнений с n неизвестными называется система вида
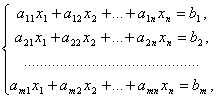
где aij и bi (i =1,…, m; b =1,…, n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы 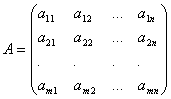 , которую назовём матрицей системы.
, которую назовём матрицей системы.
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
- Система может иметь единственное решение.
- Система может иметь бесконечное множество решений. Например,
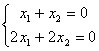 . Решением этой системы является любая пара чисел, отличающихся знаком.
. Решением этой системы является любая пара чисел, отличающихся знаком. - И третий случай, когда система вообще не имеет решения. Например,
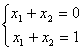 , если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Рассмотрим способы нахождения решений системы.
7. Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.
Для системы 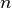 линейных уравнений с
линейных уравнений с 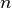 неизвестными (над произвольным полем)
неизвестными (над произвольным полем)
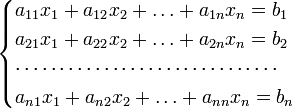
с определителем матрицы системы 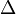 , отличным от нуля, решение записывается в виде
, отличным от нуля, решение записывается в виде
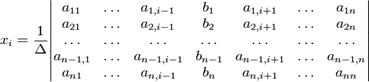
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что 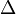 отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца(определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы
отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца(определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы 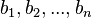 и
и 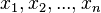 , либо набор
, либо набор 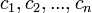 состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
Пример
Система линейных уравнений:
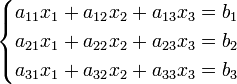
Определители:
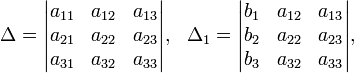
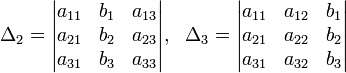
Решение:
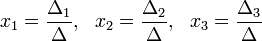
Пример:
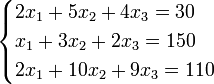
Определители:
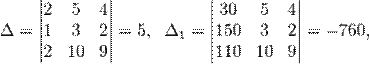
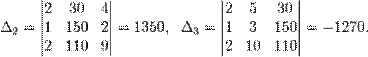
. 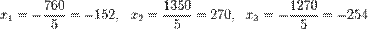
9. Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Пусть исходная система выглядит следующим образом
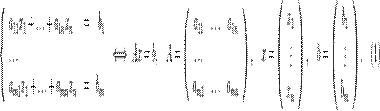
Матрица 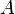 называется основной матрицей системы,
называется основной матрицей системы, 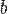 — столбцом свободных членов.
— столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
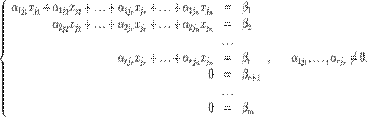
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных 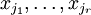 [3].
[3].
Тогда переменные 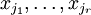 называются главными переменными. Все остальные называются свободными.
называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число 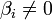 , где
, где 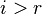 , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
, то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
Пусть 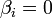 для любых
для любых 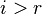 .
.
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом 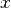 (
(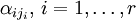 , где
, где 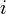 — номер строки):
— номер строки):
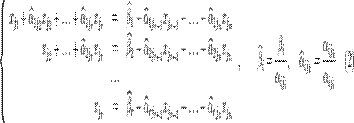 ,
,
где 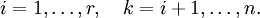
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
10. Система m линейных уравнений с n переменными имеет вид:
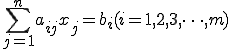 (1)
(1)
где
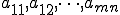
произвольные числа, называемые соответственно коэффициентами при переменных и
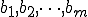
- свободными членами уравнений.
Решением системы (1) называется такая совокупность n чисел
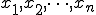 ,
,
при подстановке которых каждое уравнение системы обращается в верное равенство.
Date: 2015-08-24; view: 602; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |