
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Сложение нескольких векторов - правило многоугольника
|
|
К коллинеарным векторам это построение неприменимо.
Основываясь на рассмотренной операции сложения двух векторов, мы можем сложить три вектора и более. В этом случае складываются первые два вектора, к полученному результату прибавляется третий вектор, к получившемуся прибавляется четвертый и так далее.
Сложение нескольких векторов выполняется следующим построением. От произвольной точки А плоскости или пространства откладывается вектор, равный первому слагаемому, от его конца откладывается вектор, равный второму слагаемому, от его конца откладывается третье слагаемое, и так далее. Пусть точка B - это конец последнего отложенного вектора. Суммой всех этих векторов будет вектор формула.
Сложение нескольких векторов на плоскости таким способом называется правилом многоугольника. Приведем иллюстрацию правила многоугольника.
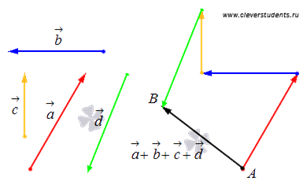
1.3. Умножение вектора на число k соответствует растяжению вектора в k раз при k > 1 или сжатию в 1/k раз при 0 < k < 1, при k = 1 вектор остается прежним (для отрицательных k еще изменяется направление на противоположное). Если произвольный вектор умножить на ноль, то получим нулевой вектор. Произведение нулевого вектора и произвольного числа есть нулевой вектор.
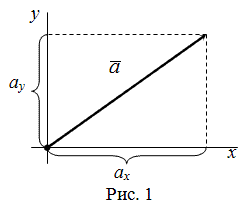
 К примеру, при умножении вектора a на число 2 нам следует вдвое увеличить его длину и сохранить направление, а при умножении вектора b на минус одну треть следует уменьшить его длину втрое и изменить направление на противоположное. Приведем для наглядности иллюстрацию этого случая.
К примеру, при умножении вектора a на число 2 нам следует вдвое увеличить его длину и сохранить направление, а при умножении вектора b на минус одну треть следует уменьшить его длину втрое и изменить направление на противоположное. Приведем для наглядности иллюстрацию этого случая.
1. Понятие матрицы. Виды матриц. Примеры.
1. Матрица - прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов.
Основные понятия матрицы:
Числа m и n называются порядками матрицы. В случае, если m=n, матрица называется квадратной, а число m=n — ее порядком.
В дальнейшем для записи матрицы будут применяться обозначение:
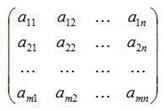
Впрочем, для краткого обозначения матрицы часто используется одна большая буква латинского алфавита, (например, А), либо символ ||aij||
Числа aij, входящие в состав данной матрицы, называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j — номер столбца.
Строка матрицы называется нулевой, если все ее элементы равны нулю.
Если хотя бы один из элементов строки матрицы не равен нулю, то строка называется ненулевой.
Столбец матрицы называется нулевым, если все его элементы равны нулю.
Если хотя бы один из элементов столбца матрицы не равен нулю, то столбец называется ненулевым.
2. Квадратной матрицей называется матрица, у которой количество строк равно количеству столбцов (размера n×n), число n называется порядком матрицы.

| -7 | 
| - квадратная матрица размера 3×3 | ||
| -1 | |||||
Нулевой матрицей называется матрица, все элементы которой равны нулю, т.е. aij = 0, ∀i, j.

| 
| - нулевая матрица | |||
Вектор-строкой называется матрица, состоящая из одной строки.

| -5 | 
| - вектор-строка |
Вектор-столбцом называется матрица, состоящая из одного столбца.

| 
| - вектор-столбец | |
| -7 | |||
Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.

| 
| - не диагональные элементы равны нулю | |||
Единичной матрицей называется диагональная матрица, диагональные элементы которой равны 1.
| E = | 
| 
| - диагональные элементы равны 1 | |||
Верхней треугольной матрицей называется матрица, все элементы которой ниже главной диагонали равны нулю.

| -6 | 
| ||
Нижней треугольной матрицей называется матрица, все элементы которой выше главной диагонали равны нулю.

| 
| |||
| -2 |
Диагональная матрица - матрица, которая одновременно является верхней треугольной и нижней треугольной.
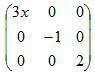
Ступенчатой матрицей называется матрица, удовлетворяющая следующим условиям:
· если матрица содержит нулевую строку, то все строки, расположенные под нею, также нулевые;
· если первый ненулевой элемент некоторой строки расположен в столбце с номером i, и следующая строка не нулевая, то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем i.

| 
| |||||
| -3 | ||||||

| 
| |||
7. Преобразования координат на плоскости. Ориентация плоскости.
1.1. Рассмотрим систему координат или репер (R), состоящая из точки О и двух базисных векторов Е1, Е2 , с помощью которых проводятся оси координат.
R= 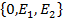
Рассмотрим еще один R̸̸ на той же плоскости R̸̸ = 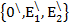
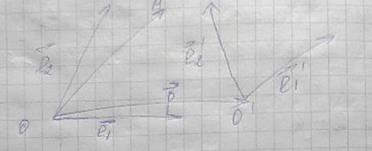
Рассмотрим вектор х на той же самой плоскости, возникает вопрос: как будут связаны между собой координаты этого вектора в 1 и во 2 базисе.
Полученные формулы будут называться формулами преобразования координат на плоскости.
Рассмотрим на плоскости точку М относительно старой системы координат, то это будут два числа (х,у)R М=(х,у)R
Берем вектор r1 , где начало О а конец М. Этот вектор расписывается по базису:
R1=xe1+ye2
Но эту точку М также рассматриваем в другом репере  М\=(х\,у\)R\
М\=(х\,у\)R\
Связь между координатами R1=xe1+ye2 и  мы должны найти.
мы должны найти.
Берем другой вектор ОО \, ОО \ - вектор переноса системы координат.
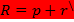 (1)
(1)
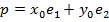
Если мы рассмотрим вектора нового базиса относительно старого базиса, то
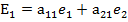
 (2)
(2)
 Эти четыре числа (а11, а12, а21, а22) либо аig, где I,g=1,2 координаты базисных векторов из нового базиса.
Эти четыре числа (а11, а12, а21, а22) либо аig, где I,g=1,2 координаты базисных векторов из нового базиса.
А т.к. базисные вектора линейно независимые, значит каждый из них ненулевой вектор и они неколлинеарные, т.е. а11 и а21 ≠ 0 или  (1 условие)
(1 условие) 
То что вектора не коллинеарные означает 
Эти условия записываются в виде палочек а внутри типо таблица, это похоже на матрицу:
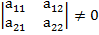
Определитель вычисляется по формуле а11*а22-а21*а22≠0
Распишем вектор (1)
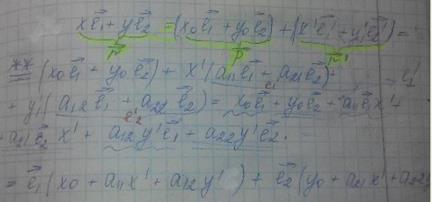

Таким образом мы получим

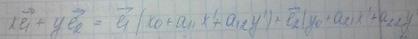
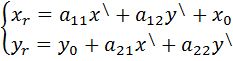
Эти формулы называются формулами преобразования координат на плоскости
Для прямоугольной декартовой системы координат эти формулы примут вид:
1 случай: Поворот
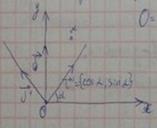
О=О\
R и R\ ортонормированы
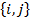 u
u 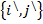
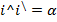
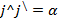
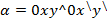
α – угол поворота системы координат
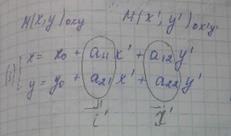
aij- координаты новых базисных векторов относительно старого базиса
В нашем случае это
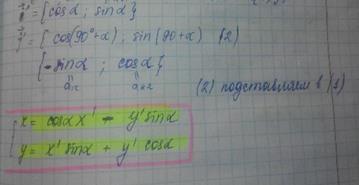
2 случай: Системы координат ортонормированы (перенос системы координат на вектор)

3 случай: Поворот с переносом
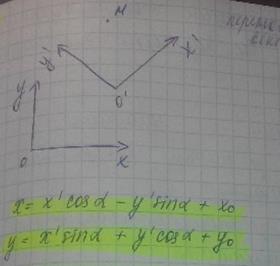
4 случай: Смена ориентации. Симметрия относительно оси
Угол идущий по часов стрелке будет отрицательной, стрелки будут отрицательными, если наоборот то положительными
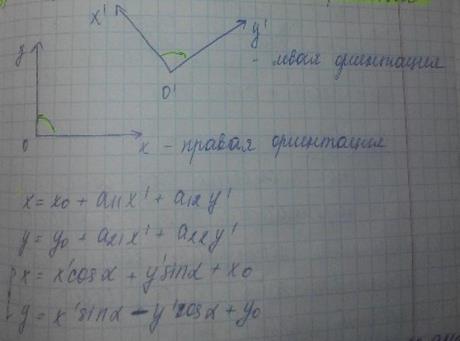
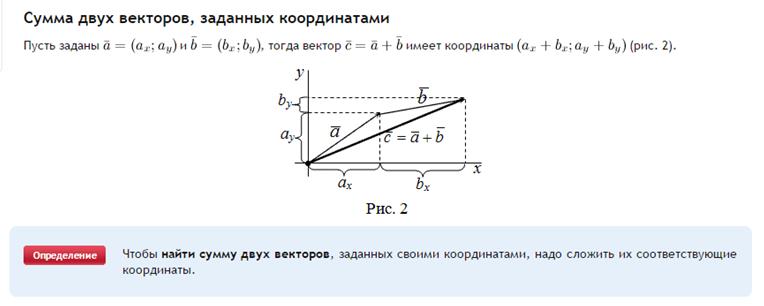
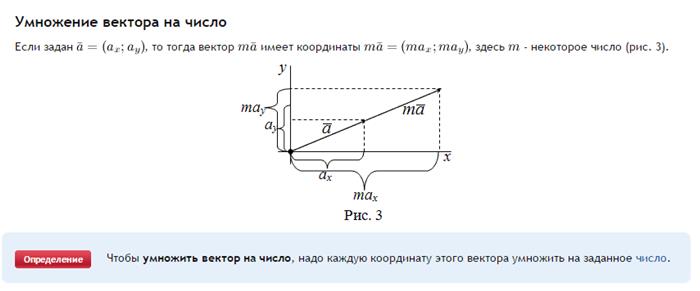
3. Координаты вектора на плоскости. Сложение векторов, умножение вектора на число в координатах.

2.  Транспонирование матриц. Свойства транспонирования. Примеры.
Транспонирование матриц. Свойства транспонирования. Примеры.

11. Применение свойств матриц и их определителей в задачах с экономическим содержанием. Примеры решения задач.
Предприятие производит три типа продукции, используя два вида ресурсов. Норма затрат ресурсов i-ого вида на производство единицы продукции j-ого типа задана матрицей затрат А, выпуск продукции за квартал- матрицей Х, стоимость единицы каждого вида ресурсов задана матрицей Р. Найти
1) Матрицу S полных затрат ресурсов каждого вида
2) Полную стоимость всех затраченных ресурсов
А= 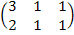 Х=
Х= 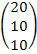 Р=
Р= 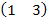
Решение.

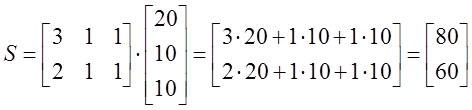
Полная стоимость ресурсов = 
Полная стоимость ресурсов = 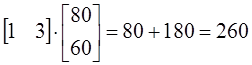
_________________________________________________________________________________
Завод производит швейные машины. Каждая машина может находиться в одном из двух состояний:
1) Работает хорошо
2) Требует регулировки.
В момент изготовления р% машин работают хорошо, (1-р)% требуют регулировки. Статистические исследования показали, что из тех машин, которые сегодня работают хорошо, через месяц 70% будут работать хорошо, а 30% потребуют регулировки. Среди тех машин, которые сегодня требуют регулировки, через месяц 60% будут работать хорошо, 40% потребуют регулировки. Каковы доли машин, которые будут работать хорошо или потребуют регулировки через месяц после их изготовления?
Р=20%
Решение:
| Работают хорошо | Требуют регулировки | |
| Момент изготовления | 20% | 80% |
| Через месяц | ||
| Те что работали хорошо | 14% (20%*0.7) | 6% (20%*0.3) |
| Те что требовали регулировки | 48% (80%*0.6) | 32 (80%*0.4) |
| Итого через месяц: | 62% (14%+48%) | 38% (6%+32%) |
Ответ: через месяц 62% машин будут работать хорошо, а 32% будут требовать регулировки
_________________________________________________________________
Дана матрица прямых затрат А. Найти изменение векторов:
А) конечного продукта 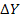 при данном изменении вектора валового продукта
при данном изменении вектора валового продукта 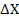
Б) валового выпуска 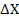 при необходимом изменении вектора конечного продукта
при необходимом изменении вектора конечного продукта 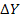
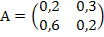
А) 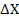 =
= 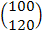 , Б)
, Б) 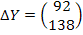
Решение:
а) 
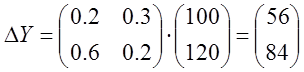
а) 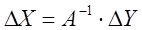
Найдем обратную матрицу. Для этого приведем матрицу A к единичной, а единичную матрицу теми же операциями к обратной.
1) 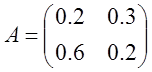
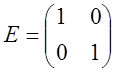
2) 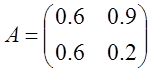
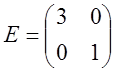
3) 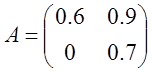
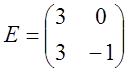
4) 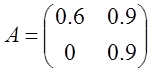
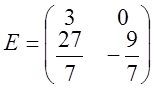
5) 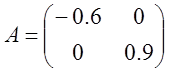
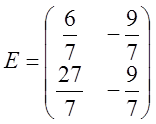
6) 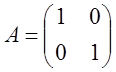
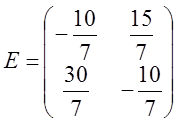
Получили обратную матрицу: 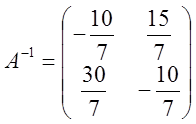
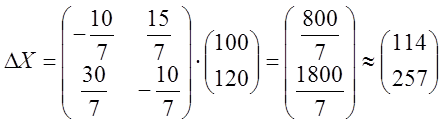
Ответ: а) 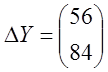 ; б)
; б) 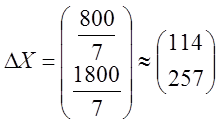
_______________________________________________________________________________________________

Решение.
(A - E)X = 0Находим собственный вектор X.
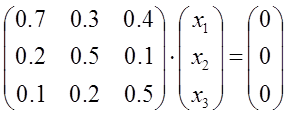
Решим систему методом Гаусса:
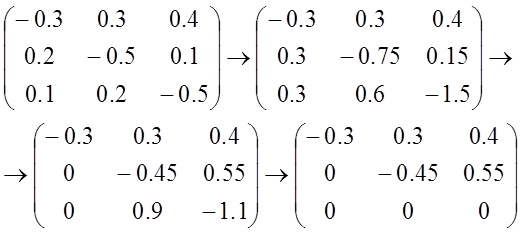
Оставим в левой части переменные x1 и x2, которые возьмем за основные. Оставшуюся (неосновную) переменную x3 перенесем в правую часть.
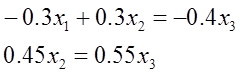
Откуда
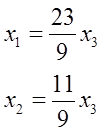
Отношения национальных доходов для сбалансированной торговли должно быть равно 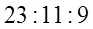
Ответ: 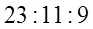
_______________________________________________________________________________________________
8.  Уравнение прямой на плоскости
Уравнение прямой на плоскости


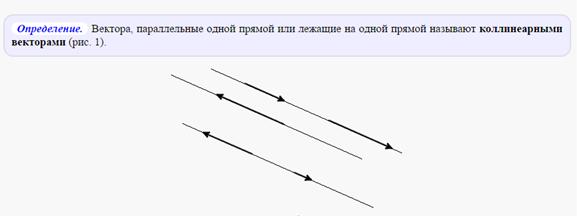
2. Линейная зависимость и независимость векторов. Векторное пространство. Коллинеарность и компланарность векторов.

Свойства линейно зависимых векторов:
- Если два вектора линейно зависимы, то они коллинеарны. Верно и обратное утверждение.
- Если три вектора линейно зависимы, то они компланарны. Верно и обратное.
-
 Четыре произвольных вектора всегда линейно зависимы.
Четыре произвольных вектора всегда линейно зависимы.

Линейное, или векторное пространство 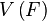 над полем
над полем 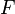 — это упорядоченная четвёрка
— это упорядоченная четвёрка 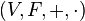 , где
, где
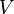 — непустое множество элементов произвольной природы, которые называются векторами;
— непустое множество элементов произвольной природы, которые называются векторами;
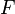 — (алгебраическое) поле, элементы которого называются скалярами;
— (алгебраическое) поле, элементы которого называются скалярами;
 — операция сложения векторов, сопоставляющая каждой паре элементов
— операция сложения векторов, сопоставляющая каждой паре элементов 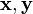 множества
множества 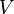 единственный элемент множества
единственный элемент множества 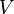 , обозначаемый
, обозначаемый 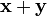 ;
;
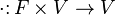 — операция умножения векторов на скаляры, сопоставляющая каждому элементу
— операция умножения векторов на скаляры, сопоставляющая каждому элементу 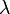 поля
поля 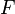 и каждому элементу
и каждому элементу 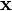 множества
множества 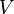 единственный элемент множества
единственный элемент множества 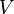 , обозначаемый
, обозначаемый 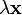 ;
;
причём, заданные операции удовлетворяют следующим аксиомам — аксиомам линейного (векторного) пространства:
1. 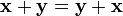 , для любых
, для любых  (коммутативность сложения);
(коммутативность сложения);
2. 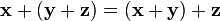 , для любых
, для любых 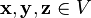 (ассоциативность сложения);
(ассоциативность сложения);
3. существует такой элемент 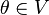 , что
, что 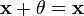 для любого
для любого 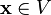 (существование нейтрального элемента относительно сложения), в частности
(существование нейтрального элемента относительно сложения), в частности 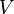 не пусто;
не пусто;
4. для любого 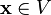 существует такой элемент
существует такой элемент 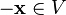 , что
, что 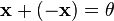 (существование противоположного элемента относительно сложения).
(существование противоположного элемента относительно сложения).
5. 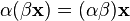 (ассоциативность умножения на скаляр);
(ассоциативность умножения на скаляр);
6. 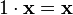 (унитарность: умножение на нейтральный (по умножению) элемент поля F сохраняет вектор).
(унитарность: умножение на нейтральный (по умножению) элемент поля F сохраняет вектор).
7. 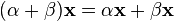 (дистрибутивность умножения на вектор относительно сложения скаляров);
(дистрибутивность умножения на вектор относительно сложения скаляров);
8. 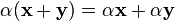 (дистрибутивность умножения на скаляр относительно сложения векторов).
(дистрибутивность умножения на скаляр относительно сложения векторов).
Таким образом, операция сложения задаёт на множестве 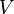 структуру (аддитивной) абелевой группы.
структуру (аддитивной) абелевой группы.
Векторные пространства, заданные на одном и том же множестве элементов, но над различными полями, будут различными векторными пространствами.
В качестве дополнительной (девятой) аксиомы векторного пространства иногда используют следующую: размерность пространства равна некоторому натуральному числу (если существует максимальная линейно независимая система векторов данного пространства или, что то же самое, существует конечная порождающая система векторов данного пространства), и тогда такое пространство называют конечномерным, или говорят, что пространство бесконечномерное (если не существует конечной порождающей системы векторов данного пространства). В соответствии с этим, теория линейных (векторных) пространств разделяется на две различные части: теорию конечномерных пространств, в которой существенным оказывается алгебраический аспект, и теорию бесконечномерных пространств, где главным оказывается аспект анализа — вопрос о разложимости данного элемента по заданной бесконечной системе функций.

 6. Алгебраическое дополнение и минор элементов матрицы.
6. Алгебраическое дополнение и минор элементов матрицы.


Date: 2015-07-27; view: 1580; Нарушение авторских прав