
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Сечения конуса. Конус является геометрическим телом, которое может иметь в сечении пять различных фигур:
Конус является геометрическим телом, которое может иметь в сечении пять различных фигур:
треугольник, если секущая плоскость пересекает конус через вершину по двум образующим (рис. 11,а и рис. 11, б);
окружность, если секущая плоскость параллельна основанию или перпендикулярна оси, а конус прямой круговой (рис.12);
эллипс, если секущая плоскость пересекает все образующие конуса под некоторым углом к основанию конуса (рис.13);
параболу, если секущая плоскость параллельна одной из образующих конуса (рис.14);
гиперболу, если секущая плоскость параллельна оси конуса или параллельна двум его образующим (рис.15).
Для того чтобы облегчить решение некоторых задач, следует применять плоскость не частного, а общего положения, проходящую через вершину.
Проекции сечений строятся обычно по точкам.
Различают две группы точек:
1 группа: опорные точки, которые выделяются особым расположением на поверхности или отношением к плоскостям проекций.
1.1. Точки видимости, расположенные на очерковых образующих поверхности и определяющие границу видимости линии на соответствующей плоскости проекций.
1.2. Точки экстремальные, т.е. точки минимального или максимального удаления от плоскости проекций.
2 группа: Точки промежуточные или случайные, уточняющие проекции кривой на чертеже.
Все опорные и промежуточные точки плоского сечения строятся с использованием их принадлежности линии данной поверхности.

Рис.11,а Рис.11,б
Рис.12 Рис.13
Рис.14 Рис.15
Эллипс
 Задача. Построить ортогональные проекции и натуральную величину сечения конуса плоскостью α ┴ П2 (рис.16)
Задача. Построить ортогональные проекции и натуральную величину сечения конуса плоскостью α ┴ П2 (рис.16)
Рис.16
Анализ:
1. Фигурой сечения является эллипс, т.к. плоскость α пересекает все образующие конуса и не перпендикулярна к оси вращения.
2. Сечение симметрично относительно плоскости σ║П2, проходящей через ось вращения конуса. Поэтому одной (двойной) точке фронтальной проекции эллипса соответствуют две симметричные точки горизонтальной и профильной проекций.
3. Фронтальной проекцией эллипса является отрезок прямой линии, совпадающий с вырожденной проекцией секущей плоскости.
4. Горизонтальной и профильной проекциями эллипса в общем случае являются эллипсы.
Решение:
1. Натуральная величина большой оси эллипса определяется отрезком А2В2 следа секущей плоскости α, заключённым между фронтальными очерковыми образующими поверхности. Прямая АВ является фронталью.
2. Находим середину отрезка А2В2. Она определяет фронтальную проекцию О2 центра эллипса и вырожденную проекцию малой оси CD.
3. Строим горизонтальные проекции точек С и D, принадлежащих данной поверхности. Отрезок СD является горизонталью, и потому его проекция С1D1 определяет натуральную величину малой оси эллипса.
4. Определяем точки Е и F эллипса, расположенные на профильных очерковых образующих поверхности конуса. Точки Е и F являются границей видимости кривой на профильной плоскости проекций.
5. Определяем промежуточные точки 1 и 2 с помощью параллели конической поверхности.
6. Выполняем окончательную обводку проекций эллиптического сечения с учётом его видимости.
7.  Строим натуральную величину эллипса методом замены плоскостей проекций.
Строим натуральную величину эллипса методом замены плоскостей проекций.
Рис.17
На рис. 17 показано построение неполного эллипса, когда секущая плоскость β пересекает основание конуса по прямой. Рис. 18 даёт изображение конуса, усеченного такой же плоскостью β, поэтому на профильной проекции вся кривая является видимой. Для наглядности плоскость среза, ограниченная эллипсом, показана заштрихованной.
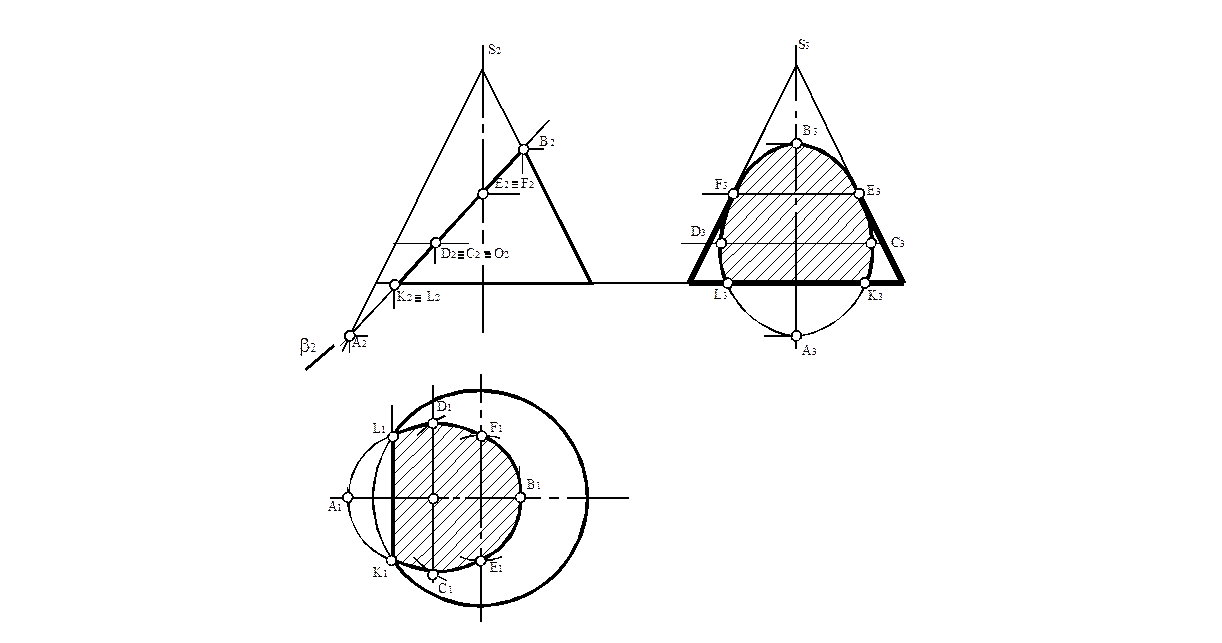
Рис.18
Date: 2015-07-24; view: 3209; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |