
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Бинарные отношения
Лекция № 4
(лек. 2 час + прак. занят 2 час + лаб. 2 час. + самос. 2 час)
ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ
Декартово произведение множеств
Одним из важных понятий теории множеств является понятие декартова (прямого) произведения множеств. Декартовым (прямым) произведением M = M1 M2 …Mn множеств Mi (i = 1…n) называется множество, элементами которого являются кортежи длиной n такие, что каждая j -ая компонента есть элемент множества Mj.
Формально: M = {‹x1, x2,...xn› xj Î Mj, j = 1,…,n}
Бинарные отношения
Последовательность длины п, члены которой суть а1,.... аn, будем обозначать через {а1,.... аn}. Последовательность {а1, а2} длины два будем называть упорядоченной парой. Декартово (прямое) произведение 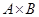 множеств А и В определяется как множество всевозможных пар {а, b}, где
множеств А и В определяется как множество всевозможных пар {а, b}, где 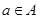 ,
, 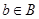 т.е.
т.е.
A×B 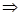 {<a,b>|a
{<a,b>|a  A&b
A&b  B}
B}
Таким образом, д екартовым произведением 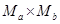 множеств Мa и Мь, называется множество М вида
множеств Мa и Мь, называется множество М вида 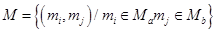 .
.
Угловыми скобками < > обозначается последовательность, т. е. множество, в котором зафиксирован порядок элементов, т.е кортеж.
Прямым (декартовым) произведением множеств А и В, обозначаемым А  В, называется множество упорядоченных пар, такое, что первая координата каждой пары — элемент А, а вторая координата — элемент В, т.е. А
В, называется множество упорядоченных пар, такое, что первая координата каждой пары — элемент А, а вторая координата — элемент В, т.е. А  В = {<a,b>| а
В = {<a,b>| а  А и b
А и b  В}.
В}.
В целях наглядного представления декартовых произведений удобно использовать язык геометрии. Для этого множества X, Y представляются осями координат. Элементы х  X, у
X, у  Y — соответственно абсциссами и ординатами. Само произведение ХÎY — точками плоскости ХОY. В качестве примера на рис. 1 показано декартово произведение множеств Х = {1, 2, 3}, Y = {1, 2}.
Y — соответственно абсциссами и ординатами. Само произведение ХÎY — точками плоскости ХОY. В качестве примера на рис. 1 показано декартово произведение множеств Х = {1, 2, 3}, Y = {1, 2}.
рис. 1
Бинарное отношение R 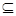 X
X  Y может отражать разный смысл.
Y может отражать разный смысл.
Пример. Значениями множества Х можно закодировать названия книжных издательств, а элементами множества Y — всех фирм некоторого региона, которые занимаются продажей этих книг. Тогда отношению R 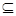 X
X  Y можно придать смысл множества заключенных договоров между издательствами и торгующими фирмами. Пусть Х={1, 2, 3}, Y={1, 2} рассматриваются как три издательства и два магазина, продающие книги. Тогда отношение R = {<1,1>, <2,2>, <3,2>} означает, что издательство 1 заключило договор с магазином 1, издательство 2 — с магазином 2, издательство 3 — с этим же магазином 2.
Y можно придать смысл множества заключенных договоров между издательствами и торгующими фирмами. Пусть Х={1, 2, 3}, Y={1, 2} рассматриваются как три издательства и два магазина, продающие книги. Тогда отношение R = {<1,1>, <2,2>, <3,2>} означает, что издательство 1 заключило договор с магазином 1, издательство 2 — с магазином 2, издательство 3 — с этим же магазином 2.
Пример. Пусть А = {1,2}, В = {а,b,с}.
Тогда А  В = {<1,а>, <1,b>, <1,с>, <2,а>, <2,b>, <2,с>}. Декартово произведение А
В = {<1,а>, <1,b>, <1,с>, <2,а>, <2,b>, <2,с>}. Декартово произведение А  В = {<а,1>, <b,2>, <с,1>, <а,2>, <b,2>, <с,2>}. Декартово произведение А
В = {<а,1>, <b,2>, <с,1>, <а,2>, <b,2>, <с,2>}. Декартово произведение А  А = {<1,1>, <1,2>, <2,1>, <2,2>} называется декартовым квадратом множества А.
А = {<1,1>, <1,2>, <2,1>, <2,2>} называется декартовым квадратом множества А.
Пример. Если множество А включает т различных элементов, а множество В — п элементов, то произведения множеств А  В и В
В и В  А имеет т п элементов. Пусть А = {1}, а В ={1,2,3}. Тогда А
А имеет т п элементов. Пусть А = {1}, а В ={1,2,3}. Тогда А  В ={< 1, 1 >, <1,2>, <1, 3 >}. Если А = 0, а В = {1, 2, 3}. Тогда А
В ={< 1, 1 >, <1,2>, <1, 3 >}. Если А = 0, а В = {1, 2, 3}. Тогда А  В=В
В=В  А=0.
А=0.
Пример 2. Всё множество координат всех клеток шахматной доски можно записать декартовым произведением вида {a,b,c,d,e,f,g,h}  {1,2,3,4,5,6,7,8} = {‹a,1›,..., ‹a,b›, ‹b,1›,..., ‹b,b›,..., ‹h,8› }
{1,2,3,4,5,6,7,8} = {‹a,1›,..., ‹a,b›, ‹b,1›,..., ‹b,b›,..., ‹h,8› }
Любое непустое подмножество R декартова произведения ХЧY множеств X,Y называется бинарным отношением между Х и Y. Записывается это так: R 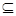 ХЧY, или так: хRу, или так: <х,у>
ХЧY, или так: хRу, или так: <х,у>  R. Слово «бинарный» происходит от английского binary, что в переводе означает «двойной». Любое непустое подмножество ХЧY является бинарным отношением на X. В частности, множество ХЧX называется универсальным отношением на X.
R. Слово «бинарный» происходит от английского binary, что в переводе означает «двойной». Любое непустое подмножество ХЧY является бинарным отношением на X. В частности, множество ХЧX называется универсальным отношением на X.
Пусть А и В два конечных множества. Напомним, что декартово произведение множеств А и В это множество АЧВ, состоящее из всех упорядоченных пар <а, b>, где а  A, b
A, b 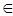 B.
B.
Бинарным отношением между элементами множеств А и В называется любое подмножество R. множества АЧВ,т.е. R 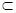 АЧВ.
АЧВ.
Под бинарным отношением (с левой областью А и правой областью В) подразумевается произвольное подмножество 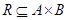 . Если А = В, то будем говорить о бинарном отношении на множестве А. Вместо
. Если А = В, то будем говорить о бинарном отношении на множестве А. Вместо 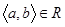 часто пишут a R b.
часто пишут a R b.
Свойства бинарных отношений.
Бинарное отношение R на множестве Х обладает следующими свойствами:
(а) рефлексивно, если х Rх для каждого 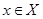 ,
,
Отношение R на множестве Х является рефлексивным, если оно выполняется между самим элементом, т.е. хRх. Пример, в отношениях «х имеет общий признак с у », «х похож на у» имеет место хRх, так как элемент х похож на самого себя.
(б) транзитивно, если  произвольных
произвольных 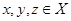 ,
,
Отношение R на множестве Х является транзитивным, если для всех 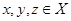 из соотношений хRу, у Rz следует хRz. Например, в отношении «операция х предшествует операции y, а операция у предшествует операции z из хRу и уRz следует хRz.
из соотношений хRу, у Rz следует хRz. Например, в отношении «операция х предшествует операции y, а операция у предшествует операции z из хRу и уRz следует хRz.
(в) симметрично, если 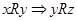 для произвольных
для произвольных 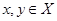 ,
,
Отношение R на множестве Х является симметричным, если для всех х,у 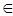 Х из хRу следует уRх. Например, в отношениях «х похож на у», «операция х несовместима с операцией у » имеет место как хRу, так и уRх. Действительно, если х похож на у, то у похож на х, если операция х несовместима с у, то операция у несовместима с х.
Х из хRу следует уRх. Например, в отношениях «х похож на у», «операция х несовместима с операцией у » имеет место как хRу, так и уRх. Действительно, если х похож на у, то у похож на х, если операция х несовместима с у, то операция у несовместима с х.
(г) антисимметрично, если 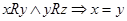 для произвольных
для произвольных 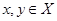 .
.
Отношение R на множестве Х является антисиммитричным, если соотношения хRу и уRх выполняются тогда и только тогда, когда х = у для всех 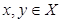 . Например, в отношении «операция х является частью операции у » имеет место хRу и уRх только тогда, когда х = у.
. Например, в отношении «операция х является частью операции у » имеет место хRу и уRх только тогда, когда х = у.
(д) антирефлексивно, если х Rх для каждого 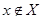 ,
,
Отношение R на множестве Х является антирефлексивным, если хRх не выполняется ни для одного хÎX. Например, в отношениях «брат х старше брата у », «операция х выполняется раньше операции у », х Rх не выполняется, так как брат х не может быть старше себя, а операция х начаться раньше самой себя.
(г) асимметрично, если 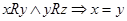 для произвольных
для произвольных 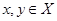 .
.
Отношение R на множестве Х является асимметричным, если из двух соотношений хRу, у Rх одно не выполнено для всех 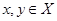 . Например, в отношениях «х подчиняется у », «операция х выполнена раньше операции у » имеет место хRу, но не выполняется уRх.
. Например, в отношениях «х подчиняется у », «операция х выполнена раньше операции у » имеет место хRу, но не выполняется уRх.
Помимо этих свойств на практике используются еще следующие:
- отношением эквивалентности,
- отношение толерантности
- отношения порядка.
Отношение эквивалентности
Отношение эквивалентности – это произвольное бинарное отношение R на множестве Х, обладающее свойствами:
- рефлексивности,
- транзитивности
- симметричности.
По смыслу отношение эквивалентности определяется как «элементы х и у одинаковы», «элементы х и у взаимозаменяемы».
В этом отношении каждый элемент эквивалентен самому себе (рефлексивность). Если элемент х эквивалентен элементу у, то и элемент у эквивалентен элементу х (симметричность). Если элемент х эквивалентен элементу у, а элемент у эквивалентен элементу z, то элемент х эквивалентен элементу z (транзитивность).
Пример 1. Отношение эквивалентности на множестве чисел является отношение равенства (=). Любое число а из множества действительных чисел равно самому себе a=a (рефлексивность). Если а=b, то b=а (симметричность). Если а=b, а b=с, то а=с (транзитивность).
Пример 2. Отношения параллельности прямых в эвклидовой плоскости.
Пример 3. Отношения проживания в одном доме жителей города.
Отношение эквивалентности разбивает любое множество на непересекающиеся подмножества (классы эквивалентности). В примере 3 все жители города разбиваются на жителей, живущих в одних и тех же домах. В результате получим столько классов эквивалентности, сколько домов, в которых проживают люди. Таким образом, если Мi, — i-й класс iÎI, а М — множество жителей, то 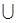 iÎIMi =M, Mi
iÎIMi =M, Mi 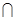 Mj=
Mj= 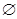 для всех i, j Î I,где I — множество классов.
для всех i, j Î I,где I — множество классов.
Отношениетолерантности
Отношение R на множестве Х называется отношением толерантности, если оно
- рефлексивно
- симметрично.
Пример. Отношение «игрок х играет сам с собой в шахматы и с другом у» есть отношение толерантности, так как хRх, а хRу влечет уRх.
Отношения порядка
А) Нестрогий порядок
Отношение R на множестве Х называется отношением нестрого порядка, если оно
- рефлексивно,
- антисимметрично
- транзитивно.
Отношения ≤, ≥ на множестве чисел Х являются отношениями нестрогого порядка, так как любое число хÎХ равно самому себе (рефлексивность).
Для любой пары чисел х,у ÎХ при а≤b не выполняется b≤a, а при а≥b не выполняется b≥a (антисимметричность).
Для любой тройки чисел х,у,zÎX, если а≤b и b≤с, то а≤с или, если а ≥b, b≥с, то а ≥с (транзитивность).
Б) Отношение частичной упорядоченности
Отношение частичной упорядоченности - это произвольное бинарное отношение, обладающее свойствами:
- рефлексивности,
- транзитивности
- антисимметричности.
Отношение частичной упорядоченности обычно обозначается через «≤», а пара <Х, ≤ > называется частично упорядоченным множеством. Будем применять также очевидные обозначения, такие как х ≥ у для у ≤ х, х <. у для 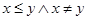 и т. д.
и т. д.
Пример. Частично упорядоченное множество. Множество целых чисел с отношением делимости, множество целых (или вещественных) чисел с обычным отношением меньше или равно «≤», а также множество Р(X) с отношением включения 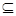 .
.
В) Отношениестрого порядка
Отношение R на множестве Х называется отношением строго порядка, если оно
- антирефлексивно,
- антисимметрично
- транзитивно.
Отношения <, > на множестве чисел Х являются отношениями строгого порядка, так как любое число хÎX не может быть меньше или больше самого себя (антирефлексивность).
Для любой пары чисел х, уÎX при х<у не может быть у<х, а при х>у не выполняется у>х (антисимметричность).
Для любой тройки чисел х,у,zÎX, если х<у, а у< z, то х< z, если х>у, а у> z, то х>z (транзитивность).
Множество Х с заданным на нем отношением нестрогого или строгого порядка R называется упорядоченным и обозначается парой < X, R>.
Если для каждой пары х, уÎX справедливо отношение строгого или нестрогого порядка, то множество < X, R> называется полностью упорядоченным. В противном случае множество < X, R> называется частично упорядоченным.
Линейный порядок
Строгий или нестрогий порядок, заданный на полностью упорядоченном множестве < X, R>, называется линейным порядком.
Пример 1. Все множества чисел линейно упорядочены, так как для любых чисел из этих множеств одно меньше другого или они равны.
Пример 2. Множество букв русского или латинского алфавита линейно упорядочено отношением предшествования, или, что то же, отношением следования.
Пример 3. Отношение подчиненности на некотором предприятии определяет строгий частичный порядок, так как в нем несравнимы сотрудники разных отделов.
Тернарные отношения
Декартовым произведением X  Y
Y  Z трех множеств X,Y,Z называется множество всех упорядоченных троек <х,у,z>, составленных из элементов этих множеств так, что X
Z трех множеств X,Y,Z называется множество всех упорядоченных троек <х,у,z>, составленных из элементов этих множеств так, что X  Y
Y  Z= {<х,у,z>| хÎХ, уÎY, zÎZ}. Любое непустое подмножество T декартова произведения X
Z= {<х,у,z>| хÎХ, уÎY, zÎZ}. Любое непустое подмножество T декартова произведения X  Y
Y  Z множеств X, Y, Z называется тернарным отношением между X, Y и Z и записывается так: Т
Z множеств X, Y, Z называется тернарным отношением между X, Y и Z и записывается так: Т 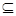 X
X  Y
Y  Z.
Z.
Пример. Трехместными отношениями Т  X
X  Y
Y  Z могут быть такие: 1) из х видов сырья у предприятий выпускают z видов продукции; 2) х покупателей покупают отоварен по z ценам; 3) но х бомбардировщикам у ракетно-зенитных комплексов дали залп z ракетами.
Z могут быть такие: 1) из х видов сырья у предприятий выпускают z видов продукции; 2) х покупателей покупают отоварен по z ценам; 3) но х бомбардировщикам у ракетно-зенитных комплексов дали залп z ракетами.
n- арные отношения
По аналогии с декартовым произведением двух множеств X,Y можно построить декартово произведение X  Y
Y  Z трех множеств X,Y,Z и вообще декартово произведение Х1
Z трех множеств X,Y,Z и вообще декартово произведение Х1  Х2
Х2  ...
...  Хn п множеств Х1,Х2,...,Хn.
Хn п множеств Х1,Х2,...,Хn.
Декартовым произведением Х1  Х2
Х2  ...
...  Хn п множеств Х1,Х2,...,Хn называется множество всех упорядоченных п - ок <х1, х2,..., xn>, составленных из элементов этих множеств так, что Х1
Хn п множеств Х1,Х2,...,Хn называется множество всех упорядоченных п - ок <х1, х2,..., xn>, составленных из элементов этих множеств так, что Х1  Х2
Х2  ...
...  Хn= {<х1, х2,..., xn>|x1
Хn= {<х1, х2,..., xn>|x1  X1, x2
X1, x2  X2, …, xn
X2, …, xn  Xn}. Любое непустое подмножество N декартова произведения Х1
Xn}. Любое непустое подмножество N декартова произведения Х1  Х2
Х2  ...
...  Хn п множеств Х1,Х2,...,Хn называется n- арным отношением между Х1,Х2,...,Хn и записывается так: N
Хn п множеств Х1,Х2,...,Хn называется n- арным отношением между Х1,Х2,...,Хn и записывается так: N  Х1
Х1  Х2
Х2  ...
...  Хn.
Хn.
В том случае, если M1 = M2 =…= Mn, то пишут Mn. Часто Mn называют универсальным отношением. Точка на плоскости может рассматриваться как упорядоченная пара, а в пространстве - упорядоченная тройка. Координатное представление впервые ввел Рене Декарт (1596-1650), поэтому оно и называется «декартово произведение».
Декартовым произведением
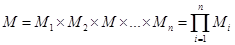
множеств М1, М2, М3,..., Мп называется множество
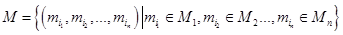 .
.
Элементами декартова произведения 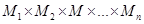 являются всевозможные последовательности, каждая из которых состоит из п элементов, причем первый элемент принадлежит множеству М1, второй — множеству М2,..., п -й элемент — множеству Мn.
являются всевозможные последовательности, каждая из которых состоит из п элементов, причем первый элемент принадлежит множеству М1, второй — множеству М2,..., п -й элемент — множеству Мn.
Теорема. Для конечных множеств A и B, мощность декартова произведения равна произведению мощностей множеств декартового произведения, т.е. | A´B | = | A | | B |
Доказательство. Первый компонент упорядоченной пары можно выбрать | A | способами, второй | B | способами. Всего упорядоченных пар <aibj> будет | A | | B | ч.т.д.
Пример 1. Сколько вариантов окраски квадрантов круга возможно, если допускается пять цветов краски.
Решение:
Кортеж длины 4, каждая компонента которого есть цвет краски, есть элемент декартового произведения. Пусть цвета краски образуют множество M = {к,б,з,с,ф}. Тогда М4 = М ´ М ´ М ´ М и çМ4ç = ç54ç = 625.
Отношения
Отображения – это некоторые связи между элементами множеств. Простейшими примерами отношений являются отношения принадлежности х  Х элемента х множеству Х и отношения включения А
Х элемента х множеству Х и отношения включения А 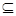 В, А
В, А 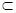 В подмножества А в подмножество В.
В подмножества А в подмножество В.
По количеству элементов, между которыми определены связи, отношения делятся на унарные (одноместные), бинарные (двухместные), тернарные (трехместные) и n -арные (n -местные). В унарном отношении участвует один элемент. Эти отношения называются свойствами и отождествляются с подмножеством элементов, которые этим свойством обладают. Так, например, в множестве всех положительных чисел отношение или свойство «быть четным» отождествляется с подмножеством чисел 2, 4, 6,....
В бинарных отношениях участвуют пары элементов множеств, так называемые упорядоченные пары <х1,у1>, <х2,у2>, х1, х2, …  Х, у1, у2, …
Х, у1, у2, …  Y. Упорядоченность понимается как то, что в записи <х,у> на первом месте всегда стоит х
Y. Упорядоченность понимается как то, что в записи <х,у> на первом месте всегда стоит х  X, а на втором у
X, а на втором у  Y. Иными словами, х предшествует у.
Y. Иными словами, х предшествует у.
Date: 2015-07-24; view: 728; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |