
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Модель идеальной жидкости. Уравнения Эйлера. Интеграл Бернулли для установившегося вихревого и безвихревого (потенциального) движения жидкости. Частные случаи вихревого движения
Билет №5
Модель идеальной жидкости. Уравнения Эйлера.
Идеальная жидкость - жидкость без вязкости. На самом деле любая жидкость вязкая. Модель идеальной жидкости применяется, если силы вязкости, действующие на ЖЧ, малы по сравнению с другими силами. Подставим в уравнения Навье-Стокса движения вязкой сжимаемой жидкости (газа) -  . Получим:
. Получим:
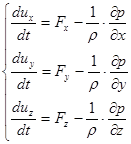 (1)
(1)
данные уравнения называются уравнениями Эйлера и описывают движение идеальной сжимаемой и несжимаемой жидкости.
Уравнение неразрывности имеет при этом выглядит:
 (2)
(2)
В векторной форме уравнения Эйлера:
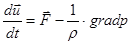 или
или 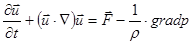 (3)
(3)
а в форме Громеки-Ламба: 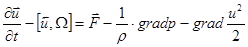 (4)
(4)
где 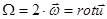 - вектор-вихрь.
- вектор-вихрь.
Для жидкости в баротропном состоянии - 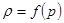 . В разделе «Гидростатика» мы ввели для баротропной жидкости функцию давления R:
. В разделе «Гидростатика» мы ввели для баротропной жидкости функцию давления R: 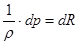 или
или 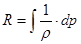 . Подставим
. Подставим 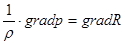 и
и 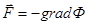 в последнее уравнение Эйлера:
в последнее уравнение Эйлера:
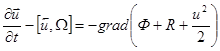 (5)
(5)
Для несжимаемой жидкости  :
:
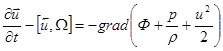 (6)
(6)
Как раньше обозначив 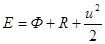 , получим:
, получим:
 (7)
(7)
Уравнения Эйлера вместе с уравнение неразрывности (4 уравнения) содержат 5 неизвестных: 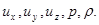 В случае несжимаемой жидкости r известно и система замкнута. Для сжимаемого газа система дополняется уравнением состояния:
В случае несжимаемой жидкости r известно и система замкнута. Для сжимаемого газа система дополняется уравнением состояния: 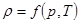 .
.
Граничные условия для идеальной и вязкой жидкости различаются. В отсутствии вязкости жидкость не прилипает к стенке, а скользит вдоль нее с собственной скоростью. Условие непроницаемости стенки имеет вид:
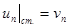 (8)
(8)
где 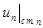 - проекция скорости жидкости на стенке по нормали к стенке;
- проекция скорости жидкости на стенке по нормали к стенке; 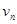 - проекция скорости стенки на нормаль к стенке.
- проекция скорости стенки на нормаль к стенке.
Уравнение Бернулли для идеальной жидкости.
1. Установившееся безвихревое (потенциальное) движение.
То есть: 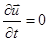 и
и 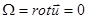 . Уравнение Эйлера (7) при этом получит вид:
. Уравнение Эйлера (7) при этом получит вид:
 Þ (9)
Þ (9)
 (10)
(10)
полученное соотношение (10) называют интегралом Бернулли.
2. Установившееся вихревое движение.
То есть: 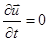 и
и 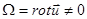 . Уравнение Эйлера (7) при этом получит вид:
. Уравнение Эйлера (7) при этом получит вид:
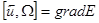 (11)
(11)
В общем случае вектора  и
и 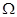 не параллельны. Умножим уравнение Эйлера (11) на вектор- дифференциал линии тока
не параллельны. Умножим уравнение Эйлера (11) на вектор- дифференциал линии тока 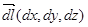 :
:
 (12)
(12)
так как 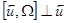 , а
, а 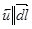 согласно свойству линии тока, то
согласно свойству линии тока, то  Þ
Þ  .
.
Кроме того, ранее было установлено: 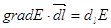
Имеем: 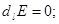 (13)
(13)
другими словами вдоль линии тока:
 (14)
(14)
получили интеграл Бернулли.
Для установившегося вихревого течения идеальной жидкости сумма 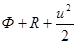 остается постоянной вдоль линий тока, а для установившегося безвихревого течения идеальной жидкости сумма
остается постоянной вдоль линий тока, а для установившегося безвихревого течения идеальной жидкости сумма 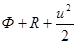 постоянна во всей области течения.
постоянна во всей области течения.
Частные случаи установившегося вихревого движения.
а) Изотермическое течение несжимаемой идеальной жидкости в поле силы тяжести.
Подставляя в (14)  и
и 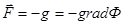 Þ
Þ  , получим:
, получим:
 (15)
(15)
б) Изотермическое течение идеального газа.
Согласно закону Бойля-Мариотта при постоянной температуре:
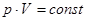 (16)
(16)
закон сохранения массы: 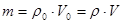 (17)
(17)
отсюда: 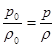 Þ
Þ  (18)
(18)
Пусть  - давление и плотность газа в некоторой точке течения.
- давление и плотность газа в некоторой точке течения.
Подставим (18) в выражение для функции давления:
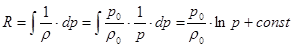 (19)
(19)
Влиянием силы тяжести для газа можно пренебречь, то есть - 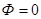 .
.
Тогда интеграл Бернулли (14) примет вид:
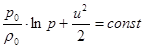 (20)
(20)
Пусть 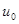 - скорость газа в точке с
- скорость газа в точке с  . Тогда получим:
. Тогда получим:
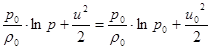 Û
Û 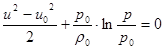 . (21)
. (21)
в) Адиабатное течение идеального газа.
Уравнение адиабатного процесса:
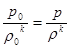 Þ
Þ  (22)
(22)
где k – показатель адиабаты (k=1.4 для воздуха).
Подставим (22) в выражение для функции давления:
 (23)
(23)
В силу невесомости газа: 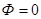 .
.
Пусть 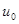 - скорость газа в точке с
- скорость газа в точке с  . Тогда интеграл Бернулли (14) примет вид:
. Тогда интеграл Бернулли (14) примет вид:
 (24)
(24)
Вопрос
Силы, действующие в жидкости. Свойства напряжений. Тензор напряжений.
НАПРЯЖЕННОЕ СОСТОЯНИЕ В ЖИДКОСТИ.
Силы, действующие в жидкости.
В жидкости действуют не сосредоточенные, а распределенные силы. По характеру действия они делятся на поверхностные и массовые (объемные).
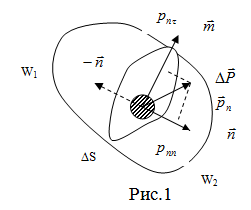
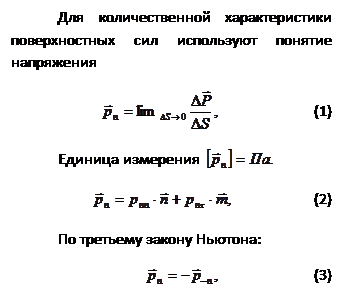
В гидромеханике принято считать положительными растягивающие напряжения, то есть направленные в сторону внешней к рассматриваемому объему нормали.
Массовые силы – это силы, действующие одинаково на каждую материальную точку ЖЧ – элементарного объема жидкости. Поэтому они не могут вызывать деформации ЖЧ, а только ее замедление или ускорение. Примерами массовых сил являются сила тяжести, электромагнитные силы, силы инерции.
Для количественной характеристики массовых сил используют следующую величину
 (4)
(4)
которая называется плотностью распределения массовых сил в точке, куда стягивается объем  Имеет размерность ускорения
Имеет размерность ускорения 
Для силы тяжести: 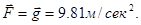
Значение поверхностной силы в точке в общем случае зависит от выбора элементарной площадки, проходящей через данную точку, а массовые силы определены однозначно.
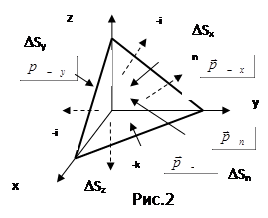
Свойства напряжений. Тензор напряжений.

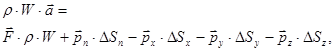 (5)
(5)
 (6)
(6)
Переходя к пределу при 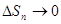 и учитывая, что
и учитывая, что 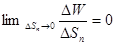 , получим:
, получим:
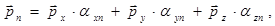 (7)
(7)
Отсюда следует, что напряжение на любой площадке DSn может быть выражено через напряжения на трех взаимно перпендикулярных площадках.
Или в проекциях на оси:
 (8)
(8)
Первый индекс указывает нормаль площадки, на которую действует напряжение, а второй индекс - ось, на которую проектируется данное напряжение. Напряжения с разноименными индексами (pxy) – касательные, с одноименными – нормальные (pxx).
То есть, напряжение на любой площадке DSn можно найти, если известна матрица:
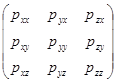 (9)
(9)
Эта матрица называется тензором напряжение (тензор второго ранга).
Записывая уравнения моментов, можно показать, что:
 (10)
(10)
- это закон парности касательных напряжений.
Таким образом, напряженное состояние в точке полностью определяется шестью величинами – тремя касательными и тремя нормальными напряжениями.
Касательные силы обусловлены действием вязкости. Поэтому касательные напряжения равны нулю в идеальной (невязкой) жидкости. Касательные напряжения равны нулю также в покоящейся жидкости. Вспомните закон трения Ньютона:  , вязкие напряжения возникают только при относительном сдвиге слоев. В этих случаях:
, вязкие напряжения возникают только при относительном сдвиге слоев. В этих случаях:
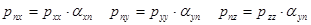 (11)
(11)
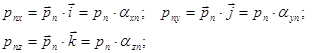 (12)
(12)
Из (10) и (12) следует:
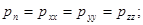 (13)
(13)
Величина:
 (14)
(14)
называется гидродинамическим давлением в идеальной жидкости, и гидростатическим давлением в покоящейся жидкости. Оно всегда положительно, так как  - напряжения сжатия.
- напряжения сжатия.
Выводы:
1. Давление в точке – скалярная величина, равная модулю напряжения сжатия в данной точке.
2. Давление не зависит от ориентации элементарной площадки в данной точке.
| <== предыдущая | | | следующая ==> |
| Дополнительное задание | | | Крупнейший автопроизводитель в мире (2007—2009) |
Date: 2015-07-24; view: 5061; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |