Тейлор қатары

Айталық, 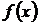функциясының кейбір нүктесі маңайында кез келген ретті туындысы

бар болсын, онда

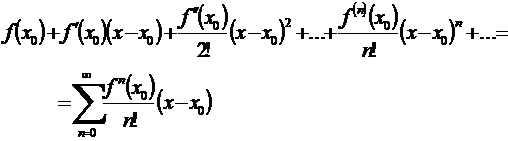(11.32)

Түрінде жазылған дәрежелік қатар нүктесіндегі Тейлор қатары деп аталады. Егер де 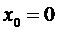болса, онда

(11.33)

Маклорен қатары деп аталады. Алынған бұл қатар нүктесінде маңайындағы жоғары да берілген 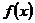функциясының орнына алынатын жуықтау өрнек ретінде қарастыруда өте жие қалданылады.

2. Қарапайым функциялардың Тейлор қатарына жіктелуі.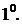

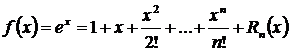
(11.41)

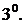
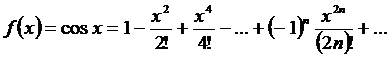(11.42)

(*)

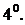
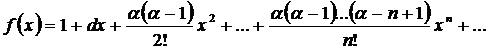М. 22 *. а) 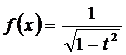, 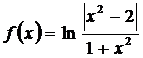функцияларын Тейлор қатарына жіктейік.

Шешуі. а)Жоғарыдағы (11.43) формуласы 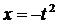, 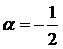деп алсақ,

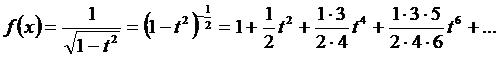
Жинақталу аймағы 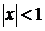болатын қатар аламыз.

Осы қатарды 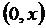аралығында мүшелеп интегралдасақ,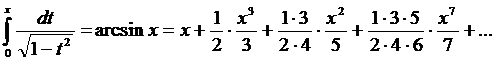 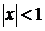болғанда жинақты жаңа қатар шығады.

ә) Берілген функцияны түрлендірейік,

.

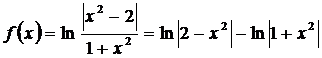Алынған екі қосылғыштарға (11.44) формуланы қолдану арқылы 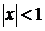болғанда:

(**)

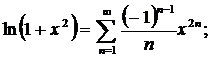
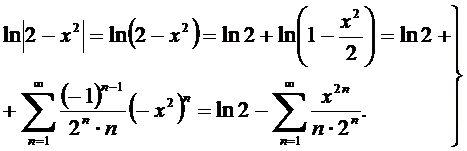Онда (*) теңдікткгі орындарына қойсақ,

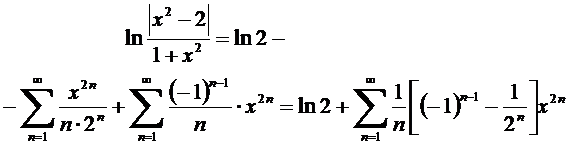
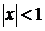болғанда жинақы болатын Тейлор қатарын аламыз.

Ескерту. Тейлор қатарының көмегімен функциялар мен интегралдарды жуықтап есептеуге болатындығын ескерткеніміз жөн.

М. 23*. а) 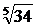шамасын 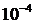- ке дейінгі, ә) 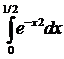интегралын 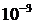─ке дейінгі дәлдікпен түрлендірейік, 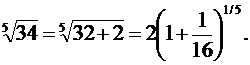Енді (11.43) биноминальдық қатарды пайдаланып, 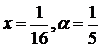деп алып, үтірден кейінгі бесінші санға дейінгі дәл келетін мүшелерін сақтаймыз. Сонымен,

(*)

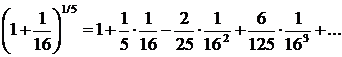таңбалары алма кезек ауысатын қатар аламыз. Бұл қатардағы 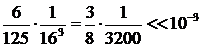болатындығын көреміз. Ендеше, (*) қатардың алтынша мүшесінен бастап ескермесекте жеткілікті. Онда

ә)Жоғарыдағы (11.38) формуладағы 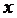-ті 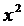-пен алмастыру арқылы,

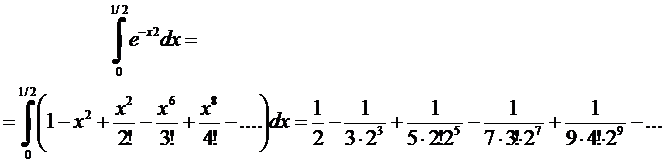Осы шексіз қосындысының алтыншы мүшесін есептесек, 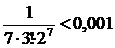екендігін көреміз. Онда берілген интегралдың 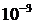-ке дейінгі алынған жуық мәні үшін шексіз қосындының алғашқа үш мүшесін алсақ жеткілікті. Сонымен,

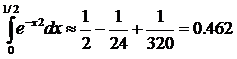
Date: 2015-07-23; view: 3963; Нарушение авторских прав