
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод последовательного уточнения оценок
Метод последовательного уточнения оценок основан, так же как и метод последовательного улучшения плана, на последовательном целенаправленном переборе базисов. Но в методе последовательного уточнения оценок перебираются двойственно допустимые базисы (и соответствующие им псевдопланы прямой задачи линейного программирования). Каждый последующий псевдоплан в этой цепочке «не хуже» предыдущего в смысле убывания значений целевой функции (которые, как известно из теории двойственности (см. [1], теорема 13.1), являются оценками сверху для оптимального значения целевой функции). Благодаря таким различиям в этих методах, метод последовательного улучшения плана часто называют прямым методом, а метод последовательного уточнения оценок – двойственным.
Начнем с получения некоторых предварительных результатов. Пусть выполняются все пред-
положения о задаче линейного программирования, сделанные в начале этого раздела.
Пусть 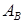 – некоторый базис,
– некоторый базис, 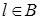 , вектор
, вектор 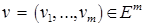 является решением следующей
является решением следующей
системы линейных алгебраических уравнений:
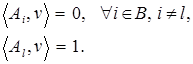 (1)
(1)
Система (1), легко увидеть, имеет единственное решение 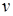 . Чтобы записать эту систему в векторно-матричном виде, положим
. Чтобы записать эту систему в векторно-матричном виде, положим 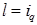 (вектор
(вектор 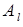 занимает в базисе позицию с номером
занимает в базисе позицию с номером 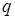 ) и обозначим через
) и обозначим через 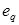 единичный орт пространства
единичный орт пространства 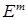 . Тогда систему (1) запишем в виде:
. Тогда систему (1) запишем в виде:
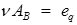 . (2)
. (2)
Далее, пусть векторы 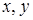 – опорные решения, соответствующие базису
– опорные решения, соответствующие базису 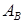 . Построим следующее однопараметрическое семейство векторов
. Построим следующее однопараметрическое семейство векторов 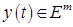 :
:
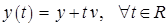 . (3)
. (3)
Установим некоторые свойства семейства векторов 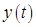 . Очевидно, что оно представляет из себя прямую в пространстве
. Очевидно, что оно представляет из себя прямую в пространстве 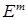 , проходящую через опорное решение
, проходящую через опорное решение  в направлении вектора
в направлении вектора 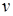 .
.
Теорема 1. Для любого базиса 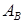 справедливо равенство
справедливо равенство
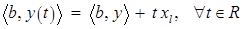 , (4)
, (4)
где 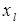 –
–  - тая координата опорного решения
- тая координата опорного решения  .
.
Доказательство. Подставляя (3) и (2) в (4) и пользуясь определением опорного решения  , для любого
, для любого 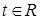 получаем
получаем
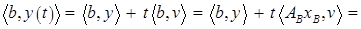
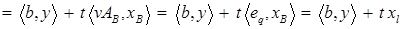 .
.
Что и требовалось.
Далее нам потребуется множество
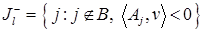 . (5)
. (5)
Теорема 2. Пусть 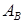 – двойственно допустимый базис,
– двойственно допустимый базис,  ,
, 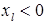 и
и 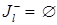 . Тогда
. Тогда 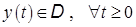 и
и 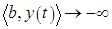 при
при 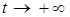 .
.
Доказательство. Для проверки включения 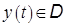 нужно убедиться в выполнении всех ограничений двойственной задачи
нужно убедиться в выполнении всех ограничений двойственной задачи 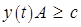 . Действительно, из включения
. Действительно, из включения 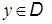 , определения вектора
, определения вектора 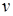 и условия теоремы
и условия теоремы 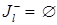 следует
следует 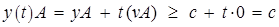 .
.
Справедливость второго утверждения теоремы следует из теоремы 1 (равенство (4)) и отрицательности 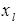 . Теорема доказана.
. Теорема доказана.
Результат, полученный в этой теореме, можно пояснить следующим образом. Полупрямая
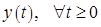 , представляет собой луч с вершиной в точке
, представляет собой луч с вершиной в точке  . В условиях теоремы вектор
. В условиях теоремы вектор  является также и вершиной (опорным планом) многогранного множества
является также и вершиной (опорным планом) многогранного множества 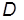 , а луч
, а луч 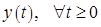 , является неограниченным ребром этого множества. Следовательно, само множество допустимых решений двойственной задачи
, является неограниченным ребром этого множества. Следовательно, само множество допустимых решений двойственной задачи 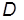 неограниченно и, как видим из второго утверждения теоремы, целевая функция двойственной задачи линейного программирования
неограниченно и, как видим из второго утверждения теоремы, целевая функция двойственной задачи линейного программирования 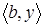 неограниченна снизу на
неограниченна снизу на 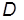 . Таким образом, теорема 2 дает набор признаков неразрешимости задач линейного программирования по причине неограниченности снизу целевой функции двойственной задачи на допустимой области. Напомним, что при этом прямая задача также не имеет решения, так как ее допустимая область пуста.
. Таким образом, теорема 2 дает набор признаков неразрешимости задач линейного программирования по причине неограниченности снизу целевой функции двойственной задачи на допустимой области. Напомним, что при этом прямая задача также не имеет решения, так как ее допустимая область пуста.
Теорема 3. Пусть 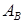 – двойственно допустимый базис
– двойственно допустимый базис  и
и  . Тогда
. Тогда 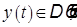
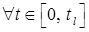 , где
, где
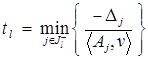 . (6)
. (6)
Доказательство. Как видим, здесь множество  , в отличие от условий теоремы 2, не пусто. Поэтому включение
, в отличие от условий теоремы 2, не пусто. Поэтому включение 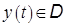 имеет место только для тех значений параметра
имеет место только для тех значений параметра 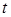 , которые удовлетворяют системе
, которые удовлетворяют системе
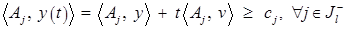 . (7)
. (7)
Разрешив неравенства (7) относительно параметра 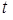 , получим
, получим 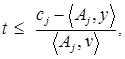 или, что то же самое,
или, что то же самое, 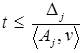 , для всех
, для всех 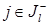 . Откуда и вытекает справедливость утверждения теоремы.
. Откуда и вытекает справедливость утверждения теоремы.
Обсудим результат, полученный в этой теореме. Множество точек 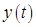 прямой (3), принадлежащих области
прямой (3), принадлежащих области 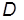 , здесь представляет из себя отрезок, который является ребром многогранного множества
, здесь представляет из себя отрезок, который является ребром многогранного множества 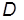 . Опорный план
. Опорный план  – одна из вершин этого ребра. Вычислим вторую вершину
– одна из вершин этого ребра. Вычислим вторую вершину 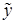 , смежную с
, смежную с  по отношению к данному ребру. Для этого вычислим
по отношению к данному ребру. Для этого вычислим 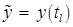 . Воспользуемся формулой (6) для максимально возможного значения параметра
. Воспользуемся формулой (6) для максимально возможного значения параметра 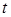 в условиях теоремы 3. Пусть в (6) минимум достигается при
в условиях теоремы 3. Пусть в (6) минимум достигается при 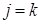 . Тогда
. Тогда 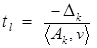 . Подставим определенное таким образом значение
. Подставим определенное таким образом значение 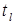 в формулу (3). Получим
в формулу (3). Получим
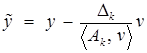 . (8)
. (8)
В силу построения, вектор 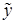 допустим для двойственной задачи. Следовательно, он удовле-
допустим для двойственной задачи. Следовательно, он удовле-
творяет всем ограничениям (неравенствам) двойственной задачи. Подставим (8) в  -тое неравенство
-тое неравенство

Таким образом, вектор 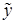 удовлетворяет
удовлетворяет  -му
-му
ограничению как равенству. Поэтому мы можем предположить, что вектор 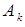 будет базисным для
будет базисным для 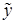 .
.
Подставим теперь вектор (8) в  -тое неравенство
-тое неравенство

Так как это ограничение может выполняться как строгое неравенство, то вектор 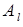 может не быть базисным для опорного решения
может не быть базисным для опорного решения 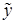 .
.
Исходя из полученного, можно предположить, что найденный вектор 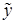 – вторая вершина построенного ребра, то есть опорный план двойственной задачи, соответствующий подсистеме
– вторая вершина построенного ребра, то есть опорный план двойственной задачи, соответствующий подсистеме 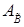 , где
, где 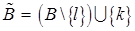 . Это предположение будет справедливо, если подсистема
. Это предположение будет справедливо, если подсистема 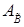 линейно независима, то есть является базисом. Этот факт устанавливается в следующей теореме.
линейно независима, то есть является базисом. Этот факт устанавливается в следующей теореме.
Теорема 4. Вектор 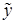 , определяемый форму-
, определяемый форму-
лой (8), является опорным планом двойственной задачи линейного программирования, соответствующим базису 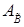 , где
, где 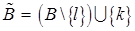 .
.
Заметим, что на основании равенства (8) имеем 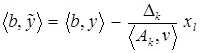 . Откуда можно сделать вывод, что при
. Откуда можно сделать вывод, что при 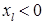 выполняется неравенство
выполняется неравенство 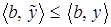 . Если же вдобавок
. Если же вдобавок 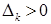 , то
, то 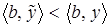 , что обеспечит уменьшение значения целевой функции при переходе из вершины
, что обеспечит уменьшение значения целевой функции при переходе из вершины  в вершину
в вершину 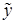 .
.
Полученные результаты позволяют сформулировать общую (принципиальную) схему метода последовательного уточнения оценок. Метод состоит из последовательного выполнения однотипных итераций. Каждая итерация осуществляет переход от текущего двойственно допустимого базиса к новому. Опишем в общем виде одну итерацию. Предположим, что имеется некоторый двойственно допустимый базис 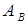 и соответствующий ему опорный план
и соответствующий ему опорный план  двойственной задачи. Далее выполняются следующие действия:
двойственной задачи. Далее выполняются следующие действия:
1. Нахождение опорного решения (псевдоплана)  , соответствующего базису
, соответствующего базису 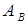 . Для этого решается система линейных алгебраических уравнений
. Для этого решается система линейных алгебраических уравнений 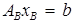 и полагается
и полагается 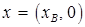 .
.
2. Проверка признака оптимальности. На
основании критерия оптимальности опорных решений (см. теорему 1.2) необходимо проверить допустимость базиса, то есть проверить выполнение неравенств
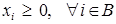 . (9)
. (9)
Возможны два случая.
a) Все неравенства (9) выполняются. Тогда векторы  и
и  являются решениями, соответственно, прямой и двойственной задач линейного программирования. На этом работа метода прекращается.
являются решениями, соответственно, прямой и двойственной задач линейного программирования. На этом работа метода прекращается.
b) Существуют значения 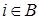 , для которых
, для которых 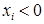 . Переходим к следующему этапу.
. Переходим к следующему этапу.
3. Выбор 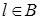 . Положим
. Положим 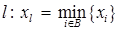 . (Очевидно, что
. (Очевидно, что 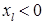 .)
.)
4. Вычисление вектора 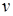 . Для этого решается система линейных алгебраических уравнений
. Для этого решается система линейных алгебраических уравнений 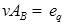 .
.
5. Построение множества значений индекса 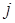 :
: 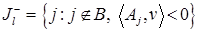 .
.
6. Проверка пустоты  . Возможны два случая.
. Возможны два случая.
a) 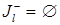 . Тогда, как следует из теоремы 2, прямая задача не имеет решения в силу пустоты допустимого множества, а двойственная задача не имеет решения в силу неограниченности снизу целевой функции на допустимом множестве. На этом работа метода прекращается.
. Тогда, как следует из теоремы 2, прямая задача не имеет решения в силу пустоты допустимого множества, а двойственная задача не имеет решения в силу неограниченности снизу целевой функции на допустимом множестве. На этом работа метода прекращается.
b) 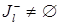 . Переходим к следующему этапу.
. Переходим к следующему этапу.
7. Выбор  . Положим
. Положим
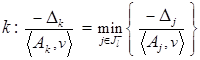 .
.
8._Построение нового базиса 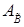 , где
, где 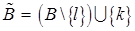 .
.
9._Пересчет обратной матрицы по формулам (7) и вычисление нового опорного плана  , соответствующего базису
, соответствующего базису 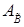 , по формулам (2.6).
, по формулам (2.6).
10._ Замена базиса 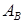 на
на 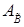 и матрицы
и матрицы 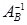 на
на 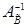 . Переход к следующей итерации, к первому ее этапу.
. Переход к следующей итерации, к первому ее этапу.
Метод обратной матрицы имеет ряд существенных преимуществ по сравнению с симплексным методом. Обратная матрица имеет меньшие размеры, чем симплексная таблица. Особенно это существенно, когда 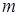 значительно меньше
значительно меньше 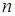 . На каждой итерации метода обратной матрицы в большей мере, чем в симплексном методе, используются данные исходной задачи линейного программирования. Поэтому в ходе большого количества итераций погрешности вычислений меньше накапливаются, что приводит к большей устойчивости этого алгоритма по сравнению с симплексным методом.
. На каждой итерации метода обратной матрицы в большей мере, чем в симплексном методе, используются данные исходной задачи линейного программирования. Поэтому в ходе большого количества итераций погрешности вычислений меньше накапливаются, что приводит к большей устойчивости этого алгоритма по сравнению с симплексным методом.
Наконец, отметим, что для отыскания исходного допустимого базиса и соответствующего ему опорного плана также возможно применение метода искусственного базиса в сочетании с методом обратной матрицы.
Date: 2015-06-12; view: 1577; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |