Примеры решения

Задача 1. Найти несущую способность растянутого элемента. Исходные данные: h = 200мм;b = 150мм; а=120мм; с=300мм; d=16мм; материал - лиственница; сорт древесины 1; условия эксплуатации А1.

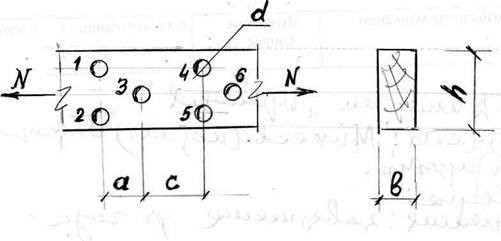
Рис. 1

Решение. Несущую способность элемента при заданных условиях задачи вычисляем по формуле

N = т₀ т_п т_в R _р A_нт

где т ₀ - коэффициент, учитывающий наличие ослаблений, равен 0,8;

т _п - коэффициент перехода на породу дерева, для лиственницы равен 1,2 [1, табл. 4];

т _в - коэффициент, учитывающий условия эксплуатации (группу конструкций), равен 1,0 [1, табл.5];

R_р - расчетное сопротивление древесины (сосны, ели), принимается по [1, табл. 3 п. 2. а] и равно 10 МПа.

Для вычисления A_нт выбираем самый опасный участок, где на расстоянии 200 мм имеет место наибольшая площадь ослаблений (не попадающих при перемещении вдоль волокон одно на другое). Такой участок будет на участке с отверстиями 1, 2 и 3.

А_нт = bh - 3db = 20•15 - 3•1,6•15 = 228 см².

Несущая способность растянутого элемента

N = 0,8•1,2•1,0•10•0,0228 = 0,21888 мН = 218,88 кН.

Задача 2. Найти несущую способность центрально-сжатого стержня

Исходные данные: h = 200мм;b = 150мм; а=150мм; ℓ =3000мм; d=40мм; материал - пихта; сорт древесины 2; условия эксплуатации А3; условия закрепленияконцов стержня в плоскостях х-х и у – у: шарнирное (Ш-Ш).

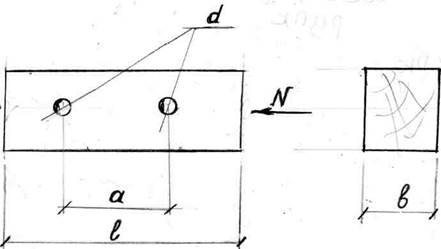
Рис. 2.

Решение. Несущая способность центрально-сжатого стержня с учетом его устойчивости подсчитывается по формуле

N =φ т_п т_в R_с A_расч

где т_п = 0,8 [1, т.4]; т_в = 0,9 [1, т.5];

R_с = 13 МПа (для сосны второго сорта) Поскольку сечение ослаблено отверстием d = 40 мм, площадь ослабления равна

А_осл = dh = 4•20 = 80 см². что составляет 100 %•80 / 20•15 = 26,7 % > 25 %.

Расчетная площадь сечения при проверке устойчивости

А_расч = (4/З) А_нт = (4/3)(300-80) = 293 см².

Для определения коэффициента φ подсчитаем гибкость элемента:

λ_х = μ_оℓ/0,289 b = 1,0•300/0,289•15 = 69,2

λ_у = μ_оℓ/0,289 h = 1,0•300/0,289•20 = 51,9

Расчет ведем на большую гибкость λ_х = 69,2

Для гибкости λ<70 определяем коэффициент φ

φ ═ 1-0,8(λ/100)² ═ 1-0,8(69,2/100) ²=0,617

Несущая способность стержня

N = 0,617•0,0293•0,8•0,9•13= 0,1692 мН = 169,2кН.

Задача 3. Проверить несущую способность центрально-сжатого стержня. Исходные данные: N = 100Кн; h = 225мм;b = 150мм; с=20мм; ℓ =4000мм; материал - сосна; сорт древесины 2; условия эксплуатации А1, условия закрепленияконцов стержня в плоскости х-х: защемление и шарнирное опирание (З-Ш) и в плоскости у – у: шарнирное опирание (Ш-Ш).

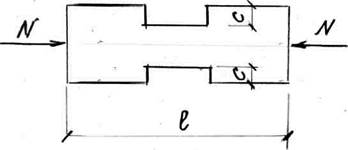
Рис. 3.

Решение. Проверка несущей способности центрально-сжатого стержня производится по формуле

N =φ т_п т_в R_с A_расч

Для рассматриваемого варианта т_п = 1,0;

т_в = 1,0;

R_с = 13 мПа.

Сечение имеет симметричное ослабление, выходящее на кромку сечения. Для такого стержня

A_расч = А_нт =(15•22,5) - 2•2•15 = 49,2 см²

Гибкость стержня

λ_х = μ_оℓ/0,289 b = 1,0•400/0,289•22,5 = 69,2

λ_у = μ_оℓ/0,289 h = 1,0•400/0,289•15 = 92.3

Наибольшая гибкость λ_у = 92.3 > 70, для нее коэффициент продольного изгиба

φ ═ 3000/ λ² ═ 3000/

Проверка несущей способности стержня:

N = 100 кН < φ т_п т_в R_с A_расч = 0,352•0,02775•1,0•1,0•13000 = 126,98 кН.

Вывод: несущая способность стержня достаточна.

ИЗГИБАЕМЫЕ ЭЛЕМЕНТЫ

Основные расчетные проверочные формулы поперечно изогнутых элементов следующие:

Ϭ ═ М/W_нт ≤ R_и;

τ ═ QS/Jb≤ R_ск или 1,5Q/bh - для прямоугольного сечения;

М/W_бр ≤ φ_м R_и; где φ_м ═ 140 k_ф b /h ℓ_р;

f/ℓ ≤ |f/ℓ|

В написанных формулах приняты следующие обозначения:

М - изгибающий момент в проверяемом сечении;

Q - поперечная сила;

J - момент инерции поперечного сечения;

W_нт - момент сопротивления нетто проверяемого сечения;

S- статический момент сдвигаемой части сечения относи­тельно нейтральной оси;

b, h - размеры поперечного сечения;

k_ф - коэффициент, учитывающий форму эпюры изгибающих моментов на участке ℓ_р, принимается по [1, при л. 4, табл.2];

R_и, R_ск - расчетное сопротивление древесины (сосны, ели), принимается по [1, табл. 3 п. 2. а];

Прогиб балки не должен превышает предельной величины, установленной [1, табл.16].

Задача 4. Проверить прочность и прогибы балки прогона цельного прямоугольного сечения. Исходные данные: q^н = 10Кн/м; h = 225мм;b = 150мм; а=1000мм; ℓ =4000мм; материал - сосна; сорт древесины 2; условия эксплуатации А1. Рис 4.

Решение. Предварительно находятся величины:

М_пр = q/2(ℓ²/4-а²) = 10/2(4²-1²) = 15кНм;

М_оп = q а²/2 = 10•1²/2 = 5кНм;

Q_пр = qℓ/2= 10•4/2 = 20кН;

Q_оп = qа= 10•1 = 10кН;

W_{нт =} bh²/6 = 15•22.5²/6 = 1265,625 см² (ослаблений нет);

S₌ bh²/8 =15•22,5²/8 = 949,22 см²;

J ₌ bh³/12 =15•22,5³/12 = 14238,281 см².

R_и = 14 МПа; R_ск =1,6 МПа.

Проверка прочности:

Ϭ ═ М/W_нт =15•10³/1265,625 = 11,85 МПа < R_и = 14 МПа;

τ ═ QS/Jb =20•10•949,22 /14238,281•15 = 0,89 МПа < R_ск = 1,6 МПа.

Прочность обеспечена.

Полный прогиб

f_о= qа(ℓ³ – 6а²ℓ-3а³)/24ЕJγ_f = 10•1•10 (4³- 6•1²•4 - 3•1³)/24•10⁵•14238,28•1,2 = 0,902 см;

где

Е = 10⁴МПа = 10⁵кгс/см² [1,п. 3.5. – модуль упругости древесины вдоль волокон].

γ_f=1,2 – усредненный коэффициент перехода к расчетам по 2-му предельному состоянию.

f_пр = qℓ²(5/8ℓ² -3а³)/48ЕJγ_f = 10•4² •10⁵(5/8 •4² - 3•1³)/48•10⁵•14238,28•1,2

=1,366 см;

Проверка прогибов: f/ℓ = 1,366/400 = 1/293 < [1/200]

Прогиб балки не превышает предельного [1, табл.16].

Задача 5. Из условия прочности подобрать размеры попе­речного сечения балки. Исходные данные: q^н = 13 кН/м; а=1100мм; ℓ =4500мм; материал - ясень; сорт древесины 2; условия эксплуатации В1. Рис 4.

Сечения принимать согласно сортаменту пиломатериалов.

Решение. Предварительно находятся величины:

М_пр = q/2(ℓ²/4-а²) = 13/2(4,5²-1,1²) = 25,04 кНм;

М_оп = q а²/2 = 13•1,1²/2 = 7,865 кНм;

Q_пр = qℓ/2= 13•4,5/2 = кН;

Q_оп = qа= 13•1,1 =14,3кН;

Находится требуемый момент сопротивления:

W_тр ═ М/ R_и т_в = 25,04•10⁴/13•1,3•10 = 1481,66 см^2;

где R_и = 13 МПа [1, табл. 3 п. 1. а];

т_п = 1,3 для ясеня [1, табл. 4 п. 6].

Задаемся шириной сечения b = 15 см. Тогда требуемая высота сечения

h_тр = √ 6W/ b = √ 6•1481,66/15 = 24,34 см ≈ 25 см.

Принимаем сечение = 15 х 25 см (см. табл.3 приложения 1).

Момент сопротивления принятого сечения

W = bh²/6 = 15•25²/6 = 1562,5 см³.

Проверка прочности:

Ϭ ═ М/W=25,04•10³/1562,5 = 16,03 МПа < R_и т_п = 13•1,3 = 16,9 МПа;

τ ═ QS/Jb = 1,5Q/bh (для прямоугольного сечения),

где Q - максимальная поперечная сила,

τ = 1.5•29,25•10/15•25 = 1,17 МПа < R_ск т_п = 1,6•1,3 = 2,56 МПа;

где R_ск = 1,6 МПа [1, табл. 3 п. 5. а];

т_п = 1,3 для ясеня [1, табл. 4 п. 6].

Прочность обеспечена.