Продукционная модель представления знаний

Продукции (наряду с сетевыми моделями) являются наиболее популярными средствами представления знаний в информационных системах. В общем виде под продукцией понимают выражение вида A ® B. Обычное прочтение продукции выглядит так: ЕСЛИ А, ТО B. Импликация может истолковываться в обычном логическом смысле, как знак логического следования B из истинного А. Возможны и другие интерпретации продукции, например, А описывает некоторое условие, необходимое, чтобы можно было совершить действие B.

Продукционная модель или модель, основанная на правилах, позволяет представить знания в виде предложений типа

«Если (условие), то (действие)».

Под условием понимается некоторое предложение — образец, по которому осуществляется поиск в базе знаний, а под действием — действия, выполняемые при успешном исходе поиска (они могут быть промежуточными, выступающими далее как условия, и терминальными или целевыми, завершающими работу системы).

При использовании продукционной модели база знаний состоит из набора правил, Программа, управляющая перебором правил, называется машиной вывода. Чаще всего вывод бывает прямой (от данных к поиску цели) или обратный (от цели для ее подтверждения – к данным). Данные — это исходные факты, на основании которых запускается машина вывода.

Если в памяти системы хранится некоторый набор продукций, то они образуют систему продукций. В системе продукций должны быть заданы специальные процедуры управления продукциями, с помощью которых происходит актуализация продукций и выполнение той или иной продукции из числа актуализированных.

В состав системы продукций входит база правил (продукций), глобальная база данных и система управления. База правил – это область памяти, которая содержит совокупность знаний в форме правил вида ЕСЛИ – ТО.

Глобальная база данных — область памяти, содержащая фактические данные (факты). Система управления формирует заключения, используя базу правил и базу данных. Существуют следующие способы формирования заключений — прямые и обратные выводы.

Правила вывода бывает удобно представлять в виде дерева решений. Граф — множество вершин, связанных дугами. Дерево — граф, не содержащий циклов.

В прямых выводах выбирается один из элементов данных, содержащихся в базе данных, и если при сопоставлении этот элемент согласуется с левой частью правила (посылкой), то из правила выводится соответствующее заключение и помещается в базу данных или исполняется действие, определяемое правилом, и соответствующим образом изменяется содержимое базы данных.

В обратных выводах процесс начинается от поставленной цели. Если эта цель согласуется с правой частью правила (заключением), то посылка правила принимается за подцель или гипотезу. Этот процесс повторяется до тех пор, пока не будет получено совпадение подцели с данными.

При большом числе продукций в продукционной модели усложняется проверка непротиворечивости системы продукций, то есть множества правил. Поэтому число продукций, с которыми работают современные системы искусственного интеллекта, как правило, не превышает тысячи.

Сильные стороны систем продукций:

модульность;

единообразие структуры (основные компоненты продукционной системы могут применяться для построения интеллектуальных систем с различной проблемной ориентацией);

естественность (вывод заключения в продукционной системе во многом аналогичен процессу рассуждения эксперта);

гибкость родовидовой иерархии понятий, которая поддерживается только как связь между правилами (изменение правила ведет за собой изменение в иерархии);

простота создания и понимания отдельных правил;

простота пополнения и модификации;

простота механизма логического вывода.

Слабые стороны систем продукций:

процесс вывода менее эффективен, чем в других системах, поскольку большая часть времени при выводе затрачивается на непроизводительную проверку применимости правил;

сложно представить родовидовую иерархию понятий;

неясность взаимных отношений правил;

сложность оценки целостного образа знаний;

отличие от человеческой структуры знаний;

отсутствие гибкости в логическом выводе.

Представление знаний с помощью продукций иногда называют «плоским», так как в продукционных системах отсутствуют средства для установления иерархий правил. Объем знаний продукционных систем растет линейно, по мере включения в нее новых фрагментов знаний, в то время как в традиционных алгоритмических системах, использующих деревья решений, зависимость между объемом база знаний и количеством знаний является логарифмической.

Имеется большое число программных средств, реализующих продукционных подход: OPS5, EXSYS RuleBook, ЭКСПЕРТ, ЭКО, G2 и др.

Моделирование сложных систем требует большого числа знаний об объекте, в том числе экспериментальных и экспертных. Для их обработки в последнее время широко используются нейронные сети.

В литературе встречаются несколько типов информационных моделей на основе нейронных сетей:

− моделирование отклика системы на внешнее воздействие;

− классификация внутренних состояний системы;

− прогноз динамики изменения системы;

− оценка полноты описания системы и определение значимости параметров системы;

− оптимизация параметров системы по отношению к заданной целевой функции;

− управление системой.

В ряде случаев нейронные сети и физико-математические модели могут составлять единую модель, например, когда внешние условия описываются уравнениями кинетики, а отклик системы – нейронной сетью. Иногда используются гибридные нейронные модели, параметры которых являются нечеткими.

В основе теории нейронных сетей лежит желание воспроизвести функции мозга при решении конкретной задачи. Однако создающиеся системы не полностью воспроизводят функции мозга, а скорее представляют математическую модель, воспроизводящую отдельные возможности человеческого мозга, по аналогии с которым искусственные нейтронные сети характеризуются следующими свойствами:

− обучение (т.е. изменение поведения в зависимости от окружающей среды);

− обобщение (реакция сети после обучения будет, до известной степени, нечувствительна к малым изменениям входящих сигналов);

− абстрагирование (способность выявления различий во входных сигналах).

О п и с а н и е б и о л о г и ч е с к о г о н е й р о н а

Из нейробиологии известно, что человеческий мозг состоит из 1010-1011 нейронов. На рис. схематично представлен один биологический нейрон. Он содержит клеточное тело и отростки (аксон и дендриты).

Клеточное тело состоит из ядра и окружающей его цитоплазмы. На внешней поверхности содержится мембрана, включающая три слоя. Она отделяет клеточное тело от окружающих его крайних окончаний аксона.

Аксон (выход) – отросток нейрона, который служит для передачи нервных импульсов к другим нейронам или эффекторным органам (мускульным волокнам, клеткам желез).

Дендриты (входы) – отростки, которые связывают нейрон с другими нейронами. Связь осуществляется через специальные контакты, называемыми синапсами.

В упрощенном виде работу нейрона можно представить так. Клеточное тело принимает входной сигнал от других нейронов через синаптические связи дендритов, преобразует его и передает выходной сигнал через аксон другим нейронам. Скорость передачи зависит и от значений входных сигналов, и от силы синаптических связей. Несмотря на то, что функция нейрона – нелинейная, нейробиологи считают, что большинство нейронов производят линейную аппроксимацию, то есть выходной сигнал нейрона пропорционален, в некоторой степени, линейной комбинации значений входных сигналов.

И с к у с с т в е н н ы й н е й р о н

Отдельный обрабатываемый элемент искусственной нейронной сети называется искусственным нейроном. Каждый нейрон производит относительно простую работу. На его вход поступает набор сигналов X = [ x 1, x 2,..., xn ], каждый из которых может быть выходом от другого нейрона или другого источника.

Каждый вход умножается на соответствующий угловой коэффициент W = [ w 1, w 2,..., wn ], который соответствует силе синапса биологического нейрона, и поступает на вход суммирующего блока, где все произведения wixi суммируются. По этой величине определяется общий вход нейрона

где θ i – пороговая величина i -го нейрона.

Для определения выхода нейрона О (рис. 9) используется функция активации

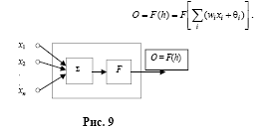
Наиболее типичными функциями активации являются:

Экспоненциальная

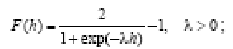
функция знака

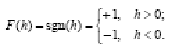
Функции, записанные в таком виде, называются биполярными. Возможно использование униполярных функций

Следует отметить, что при λ → ∞ экспоненциальная функция приближается к функции знака.

М н о г о с л о й н ы е н е й р о н н ы е с е т и

Для решения практических задач часто используются многослойные u1085 нейронные сети. Обычно в та-

ких сетях все нейроны в слое связаны со всеми нейронами в предыдущем слое через однонаправленную

связь [18]. При решении задач аппроксимации чаще используется нейронная сеть с одним скрытым слоем (рис. 10).

Многослойная нейронная сеть имеет разное количество нейронов в слоях и разные весовые коэффициенты нейронов. Каждый нейрон характеризуется множеством входов и одним выходом. Связь вход-выход для сети, представленной на рис. 10, можно представить в матричной форме

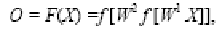
где X – вектор входных параметров; O – вектор выходных параметров;

W 1, W 2 – матрицы весовых коэффициентов для скрытого и выходного слоя, соответственно; f – функция активации. При решении задачи аппроксимации обычно используется экспоненциальная функция.

О б у ч е н и е н е й р о н н о й с е т и

Очевидно, чтобы система хорошо работала и решала практические задачи, необходимо ее обучить.

Если говорить в общем, то обучение это относительно постоянный процесс изменения поведения при поступлении жизненного опыта. Если говорить о человеке, то результат его обучения оценивается по действиям и поступкам. Обучение же нейронных сетей – более прямой процесс.

Обучение нейронных сетей рассматривается как процесс аппроксимации непрерывной функции y (X) другой функцией Y (W, X), где X = [ x 1, x 2,..., xn ] t – входной вектор, а W = [ w 1, w 2,..., wn ] t – вектор весовых коэффициентов.

Задача обучения состоит в выборе вектора W, такого что достигается лучшая аппроксимация, т.е.:

ρ (Y (W *, X), y (X)) ≤ ρ (Y (W *, X), y (X)), (8)

где ρ(Y (W, X), y (X)) – функция расстояния, которая определяет значение качества аппроксимации между Y (W, X) и y (X).

Все алгоритмы обучения делятся на две большие группы: с учителем и без учителя. Алгоритм обучения с учителем предполагает, что в каждый момент времени вместе с входами формируется желаемое значение выхода d, которое поступает от учителя. Это иллюстрируется на рис. 11.

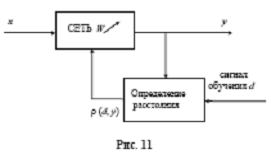
По значениям реального выхода и желаемого выхода формируется ошибка, которая используется для корректировки параметров нейронной сети. Множество входных и выходных образцов, называемых обучающим множеством, является необходимым для такого способа обучения. "Учитель" оценивает негативное направление градиента ошибки и соответственно сеть уменьшает ошибку. Во многих ситуациях, входы, выходы и вычисляемые градиенты являются детерминистическими, однако, минимизация осуществляется по случайному закону. И, как результат, большинство алгоритмов обучения с учителем используют стохастическую минимизацию ошибки в многомерном

пространстве весов.

При обучении без учителя предполагается, что значения выходов заранее не известны и поэтому информация о точной ошибке не может быть использована для настройки сети. Тогда обучение должно каким-либо образом основываться на наблюдении за входными значениями, которые получаются при обратном возвращении результата (рис. 12).

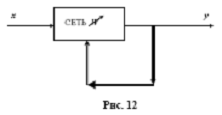
После обучения нейронная сеть обычно обладает свойствами объекта, для которого она обучалась. Теперь можно вводить любые входные значения и получать выходные данные без дополнительного обучения.