Метод Гомори

Задача целочисленного программирования может быть сформули­рована следующим образом: найти максимум или минимум функции

(7.1)

при условиях

(7.2)

_Xj > 0, j = 1, 2,..., n, а также при дополнительном условии

х_j — целые числа.

В некоторых случаях условие (7.4) распространяется только на часть переменных, такие задачи называются частично целочисленными.

Для решения задач целочисленного программирования разработа­ны специальные методы. К ним относятся метод отсечений (метод Го­мори) и метод ветвей и границ.

В основе метода Гомори заложена идея, состоящая в том, что сна­чала решается задача линейного программирования (7.1)—(7.3) без уче­та условий целочисленности. Если полученное таким образом реше­ние целочисленное, то оно принимается за оптимальный план задачи (7.I)—(7.4). Если решение нецелочисленное, то система ограничений дополняется условием, которое отсекает от множества планов задачи нецелочисленный оптимальный план, но при этом сохраняет целочис­ленные вершины множества планов. Затем решается задача линейного программирования с дополнительным условием. Если полученное та­ким образом решение целочисленное, то оно оптимально и для задачи (7.1)—(7.4). Если же и после этого не для всех переменных выполняется условие целочисленности, то вводится новое условие-отсечение. Усло­вия-отсечения выбираются таким образом, чтобы за конечное число шагов прийти к целочисленному решению, если оно у данной задачи существует. Один из алгоритмов построения таких условий-отсечений был предложен Гомори.

Рассмотрим указанный алгоритм. Пусть получено решение задачи (7.1)-(7.3) без учета целочисленности и пусть в строке r симплексной таблицы с оптимальным решением содержится нецелочисленная ком­понента опорного плана х_r0. В этом случае к условиям (7.1)—(7.3) до­бавляют условие, порожденное строкой г.

Для составления этого условия-отсечения используем г-е уравнение из последней симплексной таблицы, содержащей оптимальное реше­ние,

(7.5)

Далее введем понятие целой и дробной частей чисел а_r0 и а_rj, для чего запишем эти числа в виде:

Здесь [а_r0] и [a_rj] - целые части, a q_t, q_r] - дробные части чисел а_{r j} и a_rj.

Например, ³⁷/₃ =12 +1/3, так как [³⁷/₃] = 12, a -^s/, = -3 + 1/3„ так как [-8/3] = -3.

Из уравнения (7.5) найдем х_r

x_r=а_r0-

Теперь числа а_ю и а_rj заменим суммами целых и дробных частей:

x_r =

Предположим, что все x_j - целые числа. Тогда разность

является целым числом.

Чтобы оказалось целым числом и х_r, необходима целочисленность разности

Но О<q_г<1, 0<g_rj<1, a (7.6)

Если допустить, что разность (7.6) больше нуля, то

Однако в этом случае разность (7.6) не может быть целым числом. Сле­довательно, условие целочисленности разности может быть обеспечено только неравенством

(7.7)

Условие (7.7) и является добавочным ограничением в задаче линей­ного программирования. Для использования его в симплексном методе требуется ввести дополнительную переменную х_п+≥0, после чего не­равенство превращается в уравнение

Обычно это ограничение записывают в следующем виде:

(7.8)

Последовательно добавляя новые ограничения к решению очеред­ных задач, получаем целочисленные координаты оптимального плана задачи (7.1)—(7.4), если только не выясняется в какой-либо момент, что текущая задача не имеет решения. Это означало бы отсутствие цело­численного решения задачи (7.1)—(7.4).

Пример 1. Найти оптимальный целочисленный план задачи Z(X) = х₁ - Зх₂ + 5х₃ + 2х₄ -max

при условия

x₁+x₂+x₃ =15

2x₁+ 3x₃+x₄=8,

х_j, > 0, х_j — целые числа, j = 1, 2, 3, 4.

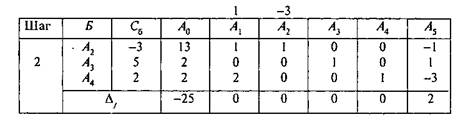
Решение. Пошаговое решение задачи приведено в табл. 7.1

Таблица 7.1

Оптимальный план задачи без условия целочисленности

X = (0, 37/3, 8/3, 0)- для дальнейшего решения задачи к таблице опти­мального плана добавлено условие

-2/3x₁-1/3x₄≤-2/3.

Номер индекса г выбран из условия большей дробной части компоненты а_i0. Имеем г = 2; j = 0: [8/3] = 2, 2 – 8/3 = -²/₃; j=1: [²/₃1 = О, О - ²/₃ ⁼ -²/₃; j = 2: [0] = 0, 0 - 0 = 0; j = 3: [0]= 0, 0 - 0 = 0; j ⁼ 4: [1/₃] = 0, 0 — 1/₃ = -1/₃. Сделав один шаг (в общем случае для получения целочисленного решения одной итерации, конечно, недоста­точно) метода последовательного уточнения оценок, получили оптимальный план целочисленной задачи Х*= (О, 13, 2, 2)

Трудоемкость решения целочисленной задачи обусловлена вводом но­вых добавочных ограничений и новых переменных. В связи с этим необ­ходимо придерживаться следующего правила, позволяющего при опре­деленных условиях сокращать текущие таблицы. Дополнительная пере­менная х_п+1 вводится в процессе решения с добавочным ограничением как базисная переменная очередного псевдоплана и сразу, на этой же итерации, переводится в число небазисных компонент. Если на дальней­ших итерациях, согласно правилу преобразования таблицы, переменная х_п+1 снова окажется базисной, ее значение станет несущественным для основных переменных задачи, так что строка и столбец текущей табли­цы, отвечающие х_п+_] вычеркиваются. Правило сокращения таблиц огра­ничивает их размеры: не более n строк и не более (2n -m) столбцов.

Рассматриваемый алгоритм целочисленного программирования сводит­ся к методу последовательного уточнения оценок с дополнительными пра­вилами расширения и сокращения текущей таблицы решения задачи.

Пример 2. Получить целочисленный оптимальный план задачи

Z(X) = x₁— 4х₂ — 2х₃ + Зх₄ —> max при условиях

3x₁+x₂+8x₃+x₄=35

x₁ +x₃+x₄≤6

x_j≥ 0, х_j — целые числа, j = 1, 2, 3, 4.

Решение. Пошаговое решение задачи приведено в табл. 7.2.

Таблица 7.2

На шаге 2 решения задачи без ограничения целочисленности полу­чаем оптимальный нецелочисленный план

X = (0, 0, 29/7, 13/7).

Поскольку обе базисные координаты X нецелочисленны, выбира­ем любую — первую или вторую — строку таблицы на шаге 2, а именно вторую, и строим добавочное ограничение

-5/7x₁-6/7x₂-1/7x₅+x₆=-6/7.

Вводя ограничение добавочной строкой на шаге 2, находим направ­ляющий элемент в этой строке:

Осуществляя преобразование табл. 7.2 с направляющим элементом (-5/7), получаем на шаге 3 оптимальный план новой задачи, снова не­целочисленный. На шаге 3 добавляем очередное условие, получаем четыре строки ограничений. Поскольку на шаге 3 достигаетсяв столбце А₆, то х₆ становится базисной переменной на шаге 4. В соот­ветствии с правилом сокращения таблицы на шаге 4 вычеркиваем стро­ку и столбец, соответствующие х₆, добавляем новую строку, а на ша­ге 5 получаем псевдоплан X = (4, 0, 3, -1). Методом последователь­ного уточнения оценок на шаге 6 получаем план, но нецелочислен­ный. Оптимальный целочисленный план получаем лишь на шаге 7: X* = (О, 1, 4, 2), max Z(X) = -6.