
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Геометрические векторы. Линейные операции с векторами
Лекции 1- 2. Векторная алгебра
Сначала вспомним известные из школьной программы определения и свойства геометрических векторов.
Определение. Геометрическим вектором называется направленный отрезок.
Обозначаем:  , А — начало, B — конец вектора.
, А — начало, B — конец вектора.

Геометрические векторы также обозначают одной буквой: 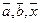 и т.п.
и т.п.

Определение. Длина вектора  — расстояние между точками A и B.
— расстояние между точками A и B.
Обозначаем:  и т.п.
и т.п.
Определение. Два вектора называются равными, если они коллинеарны (лежат на параллельных прямых), одинаково направлены и их длины равны.
Обозначаем: 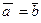 .
.

Определение. Два вектора называются противоположными, если они коллинеарны, равны по длине и противоположно направлены. Обозначаем: 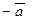 .
.

Определение. Нулевым называется вектор, имеющий нулевую длину. Направление нулевого вектора не определено. Обозначаем:  .
.
Определение. Суммой векторов  и
и  называется вектор
называется вектор 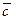 , определенный на рисунке (правило параллелограмма или правило треугольника). Обозначаем:
, определенный на рисунке (правило параллелограмма или правило треугольника). Обозначаем: 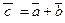 .
.

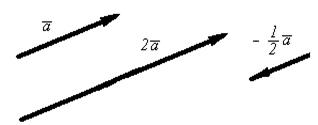
Определение. Произведением вектора  на число
на число  называется вектор длины
называется вектор длины  , коллинеарный вектору
, коллинеарный вектору  , направление которого при
, направление которого при  совпадает с направлением вектора
совпадает с направлением вектора  , а
, а  — противоположно направлению вектора
— противоположно направлению вектора  .
.
Определение. Ортом вектора  называется вектор единичной длины, направление которого совпадает с направлением вектора
называется вектор единичной длины, направление которого совпадает с направлением вектора  .
.
Обозначаем: 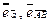 и т.п. Понятно, что
и т.п. Понятно, что  .
.
Определение. Операции сложения векторов и умножение вектора на число называются линейными операциями с векторами.
Известно (нетрудно доказать), что для линейных операций с векторами справедливо:
-
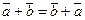 ;
; -
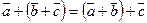 ;
; -
 ;
; -
 ;
; -
 ;
; -
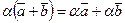 ;
; -
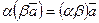 ;
; -
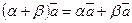 .
.
Равенства 1-8 справедливы для произвольных векторов  и для любых чисел
и для любых чисел  .
.
Декартовы координаты. Координаты вектора. Линейные операции с векторами в координатной форме
Вспомним, как определяются декартовы координаты точки в пространстве: 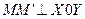 ,
, 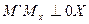 ,
,  ,
, 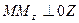 ,
,  ,
,  ,
,  —
— 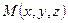 .
.

Единичные векторы координатных осей обозначаем  или
или 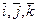 :
:

Координаты вектора  :
:  ,
,  ,
, 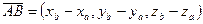 .
.
Обозначаем:  ,
,  и т.п.
и т.п.

Напомним, что координаты вектора — это ортогональные проекции вектора на координатные оси: если  , то
, то  ,
,  ,
, 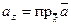 и
и  .
.
Легко видеть (по свойствам операций сложения векторов и умножения вектора на число), что если  ,
, 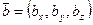 , то
, то  и
и  .
.
Действительно:
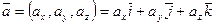 ,
, 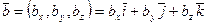 и
и 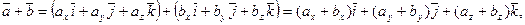 т.е.
т.е. 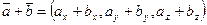 ;
;
аналогично и  , т.е.
, т.е.  .
.
Длина вектора: если  , то
, то 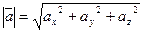 .
.
Пример. Запись 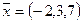 равносильна записи
равносильна записи  ;
;  .
.
Пример. Пусть  ,
, 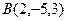 .
.
Тогда  ,
,  .
.
Определение. Вектор  называется радиусом-вектором точки A:
называется радиусом-вектором точки A:
 ,
, 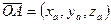
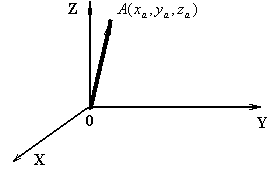
Пространство R3 арифметических векторов
Определение. Трехмерным арифметическим вектором называется упорядоченная совокупность 3 чисел. Обозначается  . Числа
. Числа  называются компонентами арифметического вектора.
называются компонентами арифметического вектора.
Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: для любых 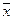 и
и  и любого числа
и любого числа  —
—  ,
,
Вектор 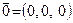 называется нулевым вектором, а вектор
называется нулевым вектором, а вектор  — противоположным вектором для вектора
— противоположным вектором для вектора 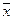 .
.
Определение. Множество трехмерных арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторовR3.
Очевидно, что для любых 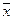 ,
,  ,
, 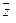 из Rn и любых чисел α, β справедливо:
из Rn и любых чисел α, β справедливо:
1.  , сложение коммутативно;
, сложение коммутативно;
2. 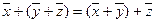 ,сложение ассоциативно;
,сложение ассоциативно;
3.  ;
;
4.  ;
;
5.  ;
;
6. 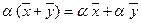 , умножение на число дистрибутивно относительно сложения векторов;
, умножение на число дистрибутивно относительно сложения векторов;
7. 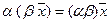 , умножение на число ассоциативно;
, умножение на число ассоциативно;
8. 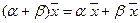 , умножение вектора на число дистрибутивно относительно сложения чисел.
, умножение вектора на число дистрибутивно относительно сложения чисел.
Мы видим, что операции сложения и умножения геометрических и трехмерных арифметических векторов имеют одинаковые свойства. Тогда можно проделать такое сопоставление:
Выберем в трехмерном геометрическом пространстве декартову систему координат. Тогда для каждого геометрического вектора 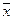 однозначно определены координаты
однозначно определены координаты  :
:  , что означает
, что означает 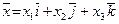 , причем, как показано выше,
, причем, как показано выше,  .
.
Это означает, что любой геометрический вектор можно рассматривать как трехмерный арифметический вектор, а пространство геометрических векторов можно изучать как пространство трехмерных арифметических векторов.
Деление отрезка в заданном отношении
Определение. Рассмотрим отрезок AB. Говорят, что точка M,принадлежащая отрезку AB делит его в отношении 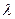 , если
, если  .
.

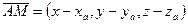 ,
,  . По известному свойству проекций если
. По известному свойству проекций если  , то
, то  , т.е.
, т.е. 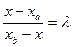 и
и  ; аналогично
; аналогично 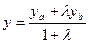 ,
,  .
.
Точка  делит отрезок
делит отрезок  ,
,
 ,
, 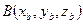 в отношении
в отношении 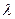 .
.
В частности, точка 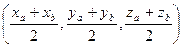 делит отрезок
делит отрезок  ,
,
 ,
, 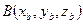 пополам (
пополам ( ).
).
Задача. Найти длину медианы треугольника ABC, проведенную из вершины A, если A (1, 0, 2), B (0,1,1), С (3, 0,-2).

Решение. Точка M — середина BC, 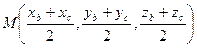 ,
,  .
.
Тогда 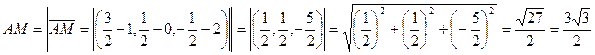 .
.
Ответ.  .
.
Скалярное произведение векторов
Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначаем:  ,
, 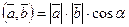 .
.

Поскольку  и
и  , то
, то 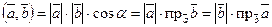

Свойства скалярного произведения. Нетрудно показать, что для произвольных векторов 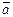 ,
,  и
и  , и для любого числа
, и для любого числа 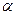 справедливо:
справедливо:
1.  ;
;
2.  ;
;
3. 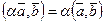 ;
;
4.  , причем
, причем 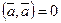 тогда и только тогда, когда
тогда и только тогда, когда  .
.
Доказательства свойств 1, 3 и 4 очевидно следуют из определения. Докажем свойство 2:  .
.
Действительно: 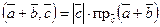 , но по известному свойству проекций
, но по известному свойству проекций  , тогда
, тогда 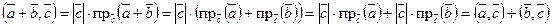 , что и требовалось доказать.
, что и требовалось доказать.
Из свойств 1- 4 можно вывести весьма важные и полезные следствия:
1. 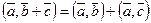 ;
;
2.  , тогда и только тогда, когда векторы
, тогда и только тогда, когда векторы  и
и  ортогональны (поскольку направление нулевого вектора не определено, его можно считать ортогональным любому вектору);
ортогональны (поскольку направление нулевого вектора не определено, его можно считать ортогональным любому вектору);
3.  ; выражение
; выражение 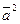 называют скалярным квадратом вектора;
называют скалярным квадратом вектора;
4. если  для любого вектора
для любого вектора 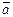 , то вектор
, то вектор  — нулевой, т.е. из
— нулевой, т.е. из  следует
следует  ;
;
5. если 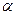 — угол между векторами
— угол между векторами 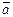 и
и  , то
, то 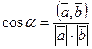 ;
;
6. если векторы  и
и  заданы своими координатами в некоторой декартовой системе координат:
заданы своими координатами в некоторой декартовой системе координат:  ,
, 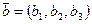 , то
, то  .
.
Следствия 1, 2, 3 и 5 очевидно следуют из определения скалярного произведения. Докажем свойство 4.
Пусть  для любого вектора
для любого вектора 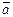 . Значит, и для
. Значит, и для  , тогда
, тогда 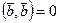 , но
, но 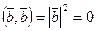 , следовательно,
, следовательно,  .
.
Докажем свойство 6 — вычисление скалярного произведения в координатах.
Если векторы  и
и  заданы своими координатами в некоторой декартовой системе координат:
заданы своими координатами в некоторой декартовой системе координат:  ,
, 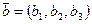 , то
, то 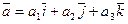 ,
, 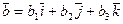 . Вычислим
. Вычислим  :
:
 , из свойства 2 и следствия 1 следует:
, из свойства 2 и следствия 1 следует:

из свойства 3 и следствия 2 следует:

поскольку 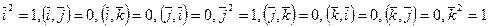 .
.
Доказано, что  .
.
Скалярное произведение векторов можно использовать для вычисления углов между векторами: если 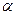 — угол между векторами
— угол между векторами 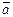 и
и  , то
, то 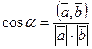 .
.
Равенство нулю скалярного произведения векторов — признак ортогональности векторов:  , тогда и только тогда, когда векторы
, тогда и только тогда, когда векторы  и
и  ортогональны.
ортогональны.
Задача (Типовой расчет!). Найти косинус угла между векторами  и
и 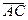 , если A (1, 2, 0), B (0, 2, -1) и C (0, 0, 1).
, если A (1, 2, 0), B (0, 2, -1) и C (0, 0, 1).
Решение.  ;
;  ,
,  ,
,  — векторы
— векторы  и
и 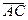 — ортогональны, угол между ними равен
— ортогональны, угол между ними равен 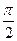 ,
,  .
.
Если не вспомнили признак ортогональности, то можно продолжать вычисления:  ,
, 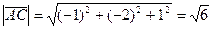 ,
, 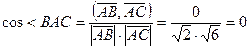 . Ответ.
. Ответ.  .
.
Задача.
Найти все внутренние углы, стороны, площадь, медианы, средние линии и высоты треугольника ABC, если A (1, 1, 0), B (0, 2, –1) и C (0, 1, –1).
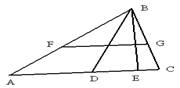
Решение. Не будем здесь приводить все вычисления. Найдем  , медиану BD, высоту BE и среднюю линию FG.
, медиану BD, высоту BE и среднюю линию FG.
 ;
; 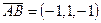 ,
,  ,
, 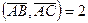 ,
, 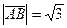 ,
,  ,
, 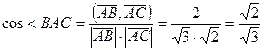 ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
D — середина AC —  ,
,  ,
,  .
.
Остальные элементы треугольника вычисляются аналогично.
B (0, 2, –1)
Определители 2-го и 3-го порядка
Определение. Определителем 2-го порядка называется число, вычисленное по квадратной таблице из 4-х чисел следующим образом:
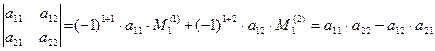 .
.
Определение. Определителем 3-го порядка называется число, вычисленное по квадратной таблице из 9-ти чисел следующим образом:
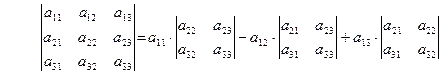 .
.
Пример.


Векторное произведение векторов
Определение. Векторным произведением векторов 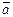 и
и  (обозначаем его
(обозначаем его 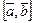 ) называется вектор, который определяется следующим образом:
) называется вектор, который определяется следующим образом:
o  ,
, 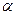 — угол между векторами
— угол между векторами 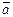 и
и  ; (определили длину вектора
; (определили длину вектора 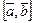 );
);
o вектор 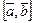 ортогонален вектору
ортогонален вектору 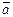 и вектору
и вектору  ; (определили положение вектора
; (определили положение вектора 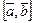 в пространстве);
в пространстве);
o векторы 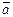 ,
,  и
и 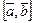 образуют правую тройку; (определили направление вектора
образуют правую тройку; (определили направление вектора 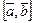 ).
).
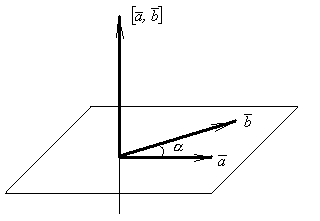
Правая тройка: из конца вектора 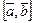 поворот от вектора
поворот от вектора 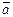 к вектору
к вектору  видится против часовой стрелки. Правую тройку хорошо «моделировать тремя первыми пальцами правой руки.
видится против часовой стрелки. Правую тройку хорошо «моделировать тремя первыми пальцами правой руки.
Важный пример.  ,
,
 ,
,
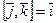 .
.
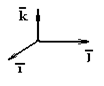
Свойства векторного произведения. Нетрудно показать, что для произвольных векторов 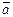 ,
,  и
и  , и для любого числа
, и для любого числа 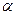 справедливо:
справедливо:
1.  ;
;
2.  ;
;
3. 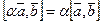 ;
;
4.  .
.
Доказательства свойств 1, 3 и 4 очевидно следуют из определения. Свойство 2 докажем чуть позже.
Из свойств 1- 4 можно вывести весьма важные и полезные следствия:
1. 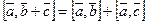 ;
;
2.  ;
;
3.  , тогда и только тогда, когда векторы
, тогда и только тогда, когда векторы  и
и  коллинеарны (лежат на параллельных прямых; нулевой вектор полагают коллинеарным любому вектору);
коллинеарны (лежат на параллельных прямых; нулевой вектор полагают коллинеарным любому вектору);
4. длина векторного произведения ( ,
, 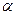 — угол между неколлинеарными векторами
— угол между неколлинеарными векторами 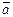 и
и  ) равна площади параллелограмма, построенного на векторах
) равна площади параллелограмма, построенного на векторах  и
и  как на сторонах;
как на сторонах;
5. если векторы  и
и  заданы своими координатами в некоторой декартовой системе координат:
заданы своими координатами в некоторой декартовой системе координат:  ,
,  , то
, то 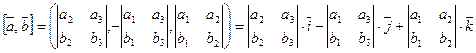 .
.
Следствия 1- 4 очевидно следуют из определения векторного произведения и его свойств. Докажем свойство 5. Доказательство совершенно аналогично доказательству формулы вычисления скалярного произведения в координатах.
Если векторы  и
и  заданы своими координатами в некоторой декартовой системе координат:
заданы своими координатами в некоторой декартовой системе координат:  ,
, 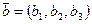 , то
, то 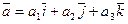 ,
, 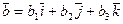 . Вычислим
. Вычислим 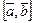 :
:

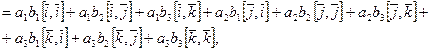
а поскольку (см. важный пример):
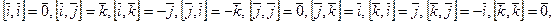 то имеем:
то имеем:


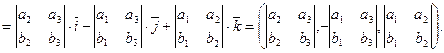
Для вычисления векторного произведения в координатах используют мнемоническую запись:

Векторное произведение векторов можно использовать для вычисления площадей параллелограммов и треугольников: углов между векторами:  ,
, 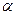 — угол между неколлинеарными векторами
— угол между неколлинеарными векторами 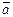 и
и  если
если 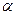 — угол между векторами
— угол между векторами 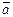 и
и  ,
, 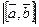 — площадь параллелограмма,
— площадь параллелограмма, 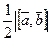 — площадь треугольника.
— площадь треугольника.
Равенство нулю векторного произведения векторов — признак коллинеарности векторов:  , тогда и только тогда, когда векторы
, тогда и только тогда, когда векторы  и
и  коллинеарны.
коллинеарны.
Задача (Типовой расчет!). Вычислить площадь параллелограмма, построенного на векторах  и
и  , если
, если  — угол между векторами
— угол между векторами  и
и  ,
, 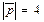 и
и 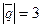 .
.
Решение. S — площадь параллелограмма.  . Воспользуемся линейностью векторного произведения (св-ва 2, 3, следствия 1, 2):
. Воспользуемся линейностью векторного произведения (св-ва 2, 3, следствия 1, 2):  а поскольку (св-ва 1 и 4)
а поскольку (св-ва 1 и 4)  , то имеем
, то имеем

Ответ.  .
.
Смешанное произведение векторов
Определение. Смешанное произведение векторов  ,
,  и
и 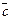 (обозначаем его
(обозначаем его 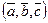 ) определяется равенством
) определяется равенством  , т.е. равно скалярному произведению векторов
, т.е. равно скалярному произведению векторов 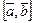 и
и  .
.
Свойства смешанного произведения. Понятно, что свойства смешанного произведения — это свойства скалярного произведения двух векторов, а поскольку первый из сомножителей, 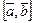 , векторное произведение, то получим суперпозицию свойств векторного и скалярного произведений.
, векторное произведение, то получим суперпозицию свойств векторного и скалярного произведений.
Например: 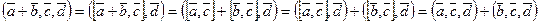 .
.
Рассмотрим только некоторые, наиболее интересные с нашей точки зрения свойства.
Признак компланарности векторов. Векторы, лежащие в одной плоскости (параллельные одной плоскости) называются компланарными векторами.
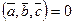 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы  ,
,  и
и 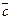 компланарны.
компланарны.
Действительно, если 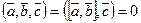 , то векторы
, то векторы 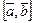 и
и 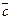 — ортогональны. Но вектор
— ортогональны. Но вектор 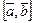 ортогонален векторам
ортогонален векторам  и
и  . Это означает, что у векторов
. Это означает, что у векторов  ,
,  и
и 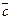 есть общий перпендикуляр, а это означает, что векторы
есть общий перпендикуляр, а это означает, что векторы  ,
,  и
и 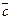 лежат в одной плоскости (параллельны одной плоскости) — компланарны. Наоборот: если векторы что векторы
лежат в одной плоскости (параллельны одной плоскости) — компланарны. Наоборот: если векторы что векторы  ,
,  и
и 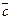 лежат в одной плоскости, то векторное произведение
лежат в одной плоскости, то векторное произведение 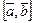 ортогонально этой плоскости, т.е. ортогонально всем векторам плоскости, т.е. ортогонально вектору
ортогонально этой плоскости, т.е. ортогонально всем векторам плоскости, т.е. ортогонально вектору 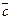 , т.е.
, т.е.  , или, что то же самое,
, или, что то же самое, 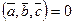 . Что и требовалось доказать.
. Что и требовалось доказать.
С помощью смешанного произведения можно вычислять объемы:  , V — объем параллелепипеда, построенного на векторах
, V — объем параллелепипеда, построенного на векторах  ,
,  и
и 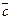 как на ребрах. Более того, если
как на ребрах. Более того, если  , то векторы
, то векторы  ,
,  и
и 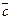 образуют правую тройку, если же
образуют правую тройку, если же  то векторы
то векторы  ,
,  и
и 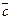 образуют левую тройку.
образуют левую тройку.
Действительно, 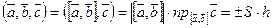 , где S — площадь основания параллелепипеда, h — высота параллелепипеда, а знак определяется направлением вектора
, где S — площадь основания параллелепипеда, h — высота параллелепипеда, а знак определяется направлением вектора 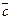 : «+» если вектор
: «+» если вектор 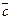 образует острый угол с плоскостью векторов
образует острый угол с плоскостью векторов  ,
,  и
и
«–», если этот угол тупой;  ,
,  — угол между векторами
— угол между векторами 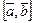 и
и 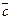 . См. рисунок.
. См. рисунок.

Ясно, что смешанное произведение позволяет вычислить объем тетраэдра, построенного на векторах  ,
,  и
и 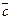 как на ребрах:
как на ребрах: 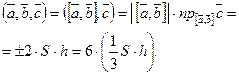 Здесь S — площадь основания тетраэдра (площадь треугольника, она равна половине
Здесь S — площадь основания тетраэдра (площадь треугольника, она равна половине  ), h —
), h —
высота тетраэдра (совпадает с высотой параллелепипеда).
См. рисунок.

Связь смешанного произведения с объемом параллелепипеда позволяет доказать нетривиальное равенство:  .
.
Действительно, легко видеть, что оба смешанные произведения равны объему одного и того же параллелепипеда (объему со знаком «–» если тройка левая). Нарисуйте соответствующую картинку и увидите.
Это последнее равенство позволяет доказать линейность векторного произведения. Посмотрите выше. Было обещано доказать
 ;
;
Действительно.  ,
,
т.е.  , откуда
, откуда  . Что и нужно было доказать.
. Что и нужно было доказать.
Вычислим смешанное произведение в координатах. Вспомните формулы для вычисления определителя 3-го порядка, формулы вычисления скалярного и векторного произведения в координатах.
Если векторы  ,
,  и
и 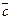 заданы своими координатами в некоторой декартовой системе координат:
заданы своими координатами в некоторой декартовой системе координат:  ,
, 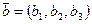 ,
, 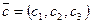 , то
, то  , а
, а

Смешанное произведение векторов можно использовать для вычисления объемов параллелепипедов:  , V — объем параллелепипеда, построенного на векторах
, V — объем параллелепипеда, построенного на векторах  ,
,  и
и 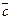 как на ребрах.
как на ребрах.
Если смешанное произведение положительно — векторы  ,
,  и
и 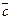 образуют правую тройку; иначе — левую.
образуют правую тройку; иначе — левую.
Равенство нулю смешанного произведения векторов — признак компланарности векторов: 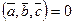 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы  ,
,  и
и  компланарны.
компланарны.
Задача (Типовой расчет!). Компланарны ли векторы 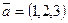 ,
, 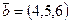 ,
, 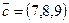 ?
?
Решение. Вычислим смешанное произведение векторов: 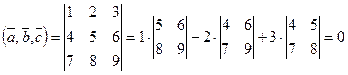 .
.
Смешанное произведение векторов равно нулю — векторы компланарны.
Ответ. Векторы компланарны.
Задача (Типовой расчет!). Вычислить объем тетраэдра с вершинами в точках A 1(1, -1, 2), A 2(2, 1, 2), A 3(1, 1, 4), A 4(6, -3, 8) и его высоту h, опущенную из вершины A4.
Решение. Вычислим смешанное произведение векторов  ,
,  , и
, и  :
:

 .
.
Тогда объем тетраэдра 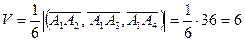 . Теперь найдем
. Теперь найдем
высоту тетраэдра h, опущенную из вершины A4 :
 ,
, 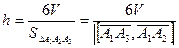 ,
, 
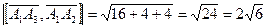 ,
, 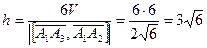 .
.
Ответ. Объем тетраэдра — 6; высота, опущенная из вершины A4, —  .
.
Задача (Типовой расчет!). Найти расстояние от точки M 0(1, -1, 2) до плоскости, проходящей через точки M 1(2, 1, 2), M 2(1, 1, 4), M 3(6, -3, 8).
Решение. Ясно, что искомое расстояние — это длины высоты тетраэдра с вершинами в точках M 0, M 1, M 2, M 3, опущенной из вершины M 0. Следовательно, решение задачи совершенно аналогично решению предыдущей задачи: вычислить объем тетраэдра (смешанное произведение), вычислить площадь основания (половина модуля векторного произведения), вычислить высоту тетраэдра.
| <== предыдущая | | | следующая ==> |
| развития ребенка от 1 до 2 лет | | | Текст для обсуждения |
Date: 2016-11-17; view: 686; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |