Диофантовы уравнения-предыстория вопроса

Диофант представляет одну из наиболее трудных загадок в истории науки. Точные годы его жизни неизвестны. Промежуток времени, когда мог жить Диофант, составляет 500 лет, хотя имеются косвенные данные о том, что Диофант жил в 3 веке в Александрии- центра научной мысли эллистического мира. Выдающийся исследователь в области собственно теории чисел, Диофант не только поставил проблему решения неопределенных уравнений в рациональных числах, но и дал некоторые общие методы их решения. При этом надо иметь в виду, что в античной математике общие методы никогда не излагались в «чистом виде», отдельно от решаемых задач (т.е. нет общего абстрактного описания этих методов). Его арифметика алгебраических кривых состоит в нахождении рациональных точек алгебраических кривых (например, кривых 2-го порядка –

рациональные решения одного алгебраического уравнения от 2-х переменных).

В “Арифметике ” Диофанта происходит окончательный отказ от геометрической алгебры. Но это вовсе не означало, что алгебра вернулась к тому состоянию, которое было у неё в Вавилоне. В “Арифметике ” алгебра обрела новый язык, гораздо более оперативный и удобный, чем язык геометрии.

Именно здесь родилась буквенная алгебра (ввел алгебраические символы для первых шести положительных и отрицательных степеней неизвестных, для обозначений вычитания и равенства), расширил числовую область для поля рациональных чисел.

Диофант был последним великим математиком античности. Античная наука и культура погасли вместе с гибелью всего античного общества.

Его методы были поняты и применены для решения новых задач Виетом и Ферма. Проблемой решения неопределенных уравнений в целых числах занимались также Эйлер, Лагранж и Лежандр (и которой продолжают заниматься и теперь).

Область математики, выросшая из задач решения неопределенных уравнений, получила название диофантова анализа (теперь чаще называют диофантовой геометрией).

Определение1. Неопределенными уравнениями 1-ой степени с с 2-мя неизвестными с целыми коэффициентами называются уравнения вида

ах +bу=с, (1) где a,b,c 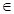Z, a 0, b 0

Уравнения с несколькими неизвестными, как правило, имеет

бесконечное множество решений, поэтому такие уравнения называются неопределенными.

В случае, если с=0, то (1) называется неоднородным (или с правой частью). Уравнение (2) с теми же значениями параметров a и b называется однородным, соответствующим данному неоднородному (1).

Одним из возможных случаев является решение уравнения (1) в области R: уравнение (1) является уравнением прямой совокупность решений уравнений (1) в R изображается прямой, если - му решению <x,y> можно поставить в соответствии точку М (x,y) этот случай относится к аналитической геометрии.

В области Q: уравнение (1) решается очень просто: полагая x=t (t-параметр, принимается всевозможные рацион. значения), из уравнения находится У= 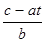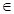Q все решения в рацион. числах имеют вид (3) x=t; У=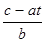

Наиболее интересным и естественным случаем является решение уравнения (1) в целых числах, которые решаются в теории чисел.

Определение 2. Решением в целых числах неопределенных уравнений (1) называется пара (х₀,у₀) целых чисел, удовлетворяющих этому уравнению (т.е числа, которые при подстановки в уравнение дают верное числовое равенство ах₀+bу₀=с).

Всякое отдельное решение (х₀,у₀) уравнения (1) называется частным; общее решение состоит из всевозможных частных (совокупность всех частных).

Итак, задача – найти все целочисленные решения уравнения (1).Соотношения (3) не могут дать в общем случае

решение этой задачи, т.к. при целочисленных значениях параметра t значения У= 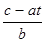не обязательно будут целыми.

Теорема 1. Неопределенное уравнение (1) первой степени с 2-мя неизвестными с целыми коэффициентами не имеет решений в целых числах, если правая часть не делится (а,b)=d

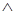
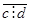
(а,b) =d >1 не имеет решений.

Доказательство: пусть (х₀,у₀) - решение уравнения (1) должно

выполнятся числовое равенство ах₀+bу₀=с т.к. (а,b)=d

c d, что противоположит условию.

Если (a,b)=d>1 и c d сократив обе части уравнения (1) на d мы получим равносильное уравнение a₁x+b₁y=c₁,где (a₁,b₁)=1, т.е этот случай сводится к уравнению: ax+by=c, где (a,b)=1

Итак, если

1⁰ (a,b)=d>1 и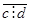

2⁰ (a,b)=d>1 и c d

3⁰ (a,b)=1 (ax+by=c) (*)