Схема Горнера. Теорема Безу

15.

Метод Фераррі. Розв’язання рівнянь 4го степеня

Розглянемо метод Феррарі розв’язування рівняння: (5)

Виділимо з перших двох доданків квадрат:

.

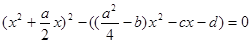1. Нехай , тоді або

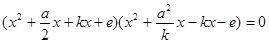і розв’язок рівняння

та 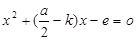будуть розв’язками рівняння (5).

2. Якщо не є квадратом, то вводимо параметр так, щоб цей вираз був квадратом (6) .

Підберемо так, щоб вираз другого доданку був квадратом (для цього дискримінант квадратного тричлена дорівнює 0).

або

(7)

Рівняння (6) називається резольвентним (розв’язуючим рівнянням) рівнянням для (5).

Знайшовши будь-який розв’язок рівняння (7) та підставивши його значення в (6), отримаємо:

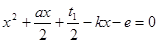та .

Розв’язки цих рівнянь будуть розв’язками рівняння (5). На практиці замість параметра часто розглядають параметр .

14.Метод Кардано. Розв’язання рівнянь 3го степеня.

Розглянемо рівняння 3-го степеня: в полі с.

Покажемо що за допомогою заміни 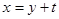можна позбутися квадрата невідомої величини. Справді:

або

. Підбедемо t так, щоб , тобто 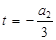, тоді одержимо:

.

Рівняння (1) називається зведеним кубічним рівнянням.

Будемо шукати розв’язок цього рівняння у виді .

Отримаємо: або . Покладемо (2) , тоді . Тобто (3)

Позначимо: , Згідно теореми Вієта і є розв’язками рівняння:

звідси

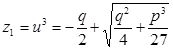
звідси ,

і (4) – формула Кардано.

Оскільки корінь третього степеня з комплексного числа має три різні комплексні значення, то з формули (4) отримаємо дев’ять комплексних чисел. Цей результат є наслідком того, що не є еквівалентним .

На практиці ми знаходимо три значення u з формули , а відповідні значення v знаходимо з умови (2) . Іноді краще знаходити значення v, а відповідні значення u знаходимо з формули (2).

5.

Алгоритм Евкліда та знаходження НСД двох многочленів

Розглянемо многочлени та 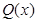над полем П.

Спільним дільником многочленів та 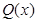називається многочлен на який діляться без остачі ці многочлени.

Найбільшим спільним дільником многочленів та 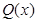називається спільний дільник, який ділиться без остачі на будь-який інший спільний дільник.

Алгоритмом Евкліда для многочленів та 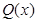є така сукупність рівностей ( - степінь многочлена :

, <

, <

, <

… …

, <

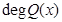
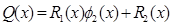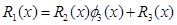Теорема Евкліда: Остання відмінна від нуль-многочлена остача алгоритму дорівнює найбільшому спільному дільнику.

Якщо многочлен ділиться на многочлен 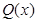, то для будь-якого сталого ділиться й на 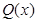. Значить алгоритм Евкліда можна застосувати з точністю до сталого множника.

6.

Кратні множники. Відокремлення кратних множників

Нехай - деякий многочлен над полем П.

Похідною многочлена називається многочлен .

Вважаємо, що похідна многочлена нульового степеня і нуль-многочлена є нуль-многочлен.

Елемент поля П називається коренем многочлена , якщо .

Елемент поля П називається 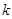-кратним коренем якщо ділиться без остачі на і не ділиться на .

Для того щоб елемент поля П був коренем кратності 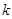многочлена необхідно і достатньо, щоб .

Позначимо 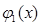добуток всіх незвідних множників першої кратності через 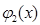- добуток всіх незвідних множників другої кратності і так дальше. Тоді

(1).

Запис многочлена у виді (1) називається відокремленням кратних множників.

Будь-який многочлен над полем П характеристики 0 можна відокремити кратні множники за допомогою скінченого числа раціональних дій над деякими многочленами.

Схема знаходження многочленів задається таблицею:

	...	...
...

 

 

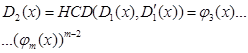
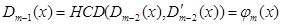
12.

Знаходження раціональних коренів многочлена

Розглянемо рівняння 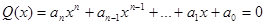(1) з цілими коефіціентами.

Теорема 1. Для того щоб раціональне число було розв’язком рівняння (1) необхідно щоб було дільником вільного члена , - дільником старшого коефіціента .

Наслідок. Якшо старший коефіціент , то всі раціональні розв’язки рівняння (1) є цілі числа, як – дільники вільного члена .

Теорема 2. Для того щоб було раціональним розв’язком рівняння (1) необхідно, щоб при довільному цілому .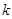

На практиці 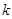фіксують .

Зауваження. При розв’язуванні алгебраїчних рівнянь доцільно використовувати схему Горнера.

1.

Кільце многочленів.

Теорема: Сукупність всіх многочленів над даним полем П утворює комутативне кільце з 1 без дільників нуля.

Доведення:

Вимоги:

1. P(x) + Q(x) = Q(x) + P(x)

2. (P(x) + Q(x)) + R(x) = P(x) + (Q(x) + R(x))

3. P(x) * Q(x)= Q(x) * P(x)

4. (P(x) * Q(x)) * R(x) = P(x) * (Q(x) * R(x))

5. P(x) * (Q(x) + R(x)) = P(x) * Q(x) + P(x) * R(x)

6. P(x) = 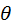, Q(x)=0-многочлен (існування 0-мног.)

7. Кожен многочлен Р(х) має протилежний –Р(х)

8. 1*Р(х) = 1

Так, як значення многочлену над полем П є елементом поля П, а поле не має дільників 0,то кільце многочленів немає дільників 0.

2.

Теорема про тотожну рівність многочлена нулеві

Теорема. Якщо поле П має менше (n+1) різних елементів, то для того, щоб многочлен тотожно дорівнює 0(приймав нулеві значення для кожного елемента поля П) необхідно і достатньо,щоб всі його коефіцієнти дорівнювали 0.

Доведення. Необхідність. Задано тотожну рівність нулеві.

,

…

(1)

Одержали лінійну однорідну алгебраїчну систему рівнянь, яка містить(n+1)рівняння, та (n+1) невідому.

Згідно теореми Крамера, система (1) має єдиний розв’язок.

Достатність. Задано,що всі коефіцієнти нулі, тобто (2)

Очевидно,що при будь-якому значенні х, .

Теорема доведена.

Зауваження. Рівність многочленів P(x) = Q(x) розуміємо,як тотожну рівність многочленів, в деяких випадках будемо записувати P(x) Q(x).

3.

Теорема про ділення з остачею.

Теорема. Для будь-якого Р(х) і не нульового многочлена Q(x) існує,і при тому єдина пара многочленів Ф(x) i R(x). P(x)= Q(x)*Ф(x)+R(x) і при чому ,то R(x)=Q(x)

Доведення.

1.

.

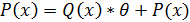2.

.

/

,

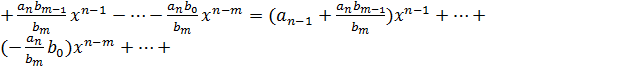є многочлен, степінь якого n-1 і згідно 2го пункту м.м.і.

Q₁(x)= Q₁(x)*Ф₁(x)+R₁(x), 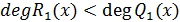, R₁(x)=

3. , P(x)= Q(x)*Ф(x)+R(x), , R(x)=0,

P(x)= Q(x)*Ф₁(x)+R₁(x), , ,

Q(x)(Ф(х)-Ф₁(х))=R₁(x)-R(x) многочлена правої частини менший степеня лівої і така рівність можлива тільки тоді,коли права частина 0-многочлен. Маємо, що R₁(x)=R(x), тоді Q(x)(Ф(х)-Ф₁(х))=0

4.

Схема Горнера. Теорема Безу.

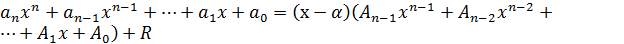. Звернемо увагу на те,що останнє в цьому разі є многочлен нулевого степеня,тобто сталим числом.

, , …,a₁=A₀- , a₀=R-

, , …, A₀= a₁ + , R = a₀+ (2)

Формули (2) показують, що поділити многочлен на ( можна за такою схемою,що називають схемою Горнера.

				…
α				…	a1 + A0	a0+ R

Виконуючи ділення за цією схемою, кожній наступний коефціент , частку і остачу R дістають множенням щойно обчисленого коефіцієнта і додавши до знайденого добутку відповідний коефіцієнт даного многочлена.

Теорема Безу. Для будь-якого числа 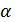з поля П остача при діленні многочлена Р(х) належить полю П на (х- і дорівнює R .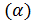

Доведення.

За формулою 1 ділення з остачею маємо Р(х)=(х- Ф(х)+R (3)

Многочлен R є стлою величиною, бо має степінь нижчий за степінь (х- Підставляючи в формулу (3) значення (х 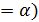дістанемо Р( =R, що й треба було довести.

7.

Розклад многочлена за степенями (х-

Нехай Р(х) многочлен n-го степеня над полем П, з цього поля. Ділення на (х- дає

Р(х)= (х- (4), де 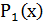–многочлен (n-1) степеня з поля P(x), a C₀-число з поля П, якщо n<1, маємо

(5)

Очевидно, що є многочленом мулевого степеня, покладеного , виключаючи з формули (4)і(5)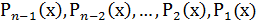

Отримуємо, (х- (х- 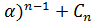(х- (х-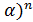

10. Теорема Вієтта.

Теорема 1. Якщо розв’язки рівняння , то ;

Теорема 2. Якщо розв’язки даного рівняння , то мають місце формули Вієтта

Доведення. Згідно основної теореми алгебри . Рівність многочленів є завжди тотожною рівністю. Два многочлени тотожно рівні тоді і тільки тоді, коли рівні коефіцієнти при відповідних степенях рівняння.

,

.

.

.

Теорема 3. Якщо є розв’язками рівняння n-го степеня, то мають місце формули Вієтта .

Доведення. Проводиться аналогічно до випадку 3-го степеня.

Date: 2016-05-25; view: 1038; Нарушение авторских прав