
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Коэффициент множественной корреляции
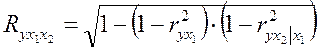 =0,9643.
=0,9643.
Следовательно, зависимость  от
от  и
и  характеризуется как очень тесная, в которой
характеризуется как очень тесная, в которой  =93% вариации затрат на выпуск продукции определяются вариацией учтенных в модели факторов: объема произведенной продукции и расходов на сырье. Прочие факторы, не включенные в модель, составляют соответственно 7% от общей вариации
=93% вариации затрат на выпуск продукции определяются вариацией учтенных в модели факторов: объема произведенной продукции и расходов на сырье. Прочие факторы, не включенные в модель, составляют соответственно 7% от общей вариации 
Скорректированный коэффициент множественной детерминации  =0,9182 указывает на тесную связь между результатом и признаками.
=0,9182 указывает на тесную связь между результатом и признаками.
3) Оценим надежность уравнения регрессии в целом с помощью 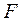 -критерия Фишера. Вычислим
-критерия Фишера. Вычислим  =79,62.
=79,62.  =3,89 определяем по таблице
=3,89 определяем по таблице 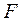 -критерия Фишера (таблица 1 приложения) взяв
-критерия Фишера (таблица 1 приложения) взяв 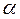 =0,05,
=0,05, 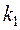 =2,
=2,  =15-2-1=12 либо с помощью встроенной статистической функции FРАСПОБР с такими же параметрами.
=15-2-1=12 либо с помощью встроенной статистической функции FРАСПОБР с такими же параметрами.
Так как фактическое значение больше табличного, то с вероятностью 95% делаем заключение о статистической значимости уравнения множественной линейной регрессии в целом.
Оценим целесообразность включения фактора  после фактора
после фактора  и
и  после
после  с помощью частного
с помощью частного 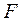 -критерия Фишера
-критерия Фишера
 =22,41;
=22,41;  =1,6.
=1,6.
 =4,75 при
=4,75 при 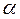 =0,05,
=0,05, 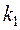 =1,
=1,  =12. Так как
=12. Так как  =22,41>
=22,41>  =4,75, а
=4,75, а  =1,6<
=1,6<  =4,75, то включение фактора
=4,75, то включение фактора  в модель статистически оправдано и коэффициент чистой регрессии
в модель статистически оправдано и коэффициент чистой регрессии  статистически значим, а дополнительное включение фактора
статистически значим, а дополнительное включение фактора  после того, как уже введен фактор
после того, как уже введен фактор  нецелесообразно.
нецелесообразно.
Низкое значение  (немногим больше 1) свидетельствует о статистической незначимости прироста
(немногим больше 1) свидетельствует о статистической незначимости прироста  за счет включения в модель фактора
за счет включения в модель фактора  после фактора
после фактора  Это означает, что парная регрессионная модель зависимости затрат на выпуск продукции от объема произведенной продукции является достаточно статистически значимой, надежной и что нет необходимости улучшать ее, включая дополнительный фактор
Это означает, что парная регрессионная модель зависимости затрат на выпуск продукции от объема произведенной продукции является достаточно статистически значимой, надежной и что нет необходимости улучшать ее, включая дополнительный фактор  (расходы на сырье).
(расходы на сырье).
3. Решение задач с помощью электронных таблиц Excel
Сводные данные основных характеристик для одного или нескольких массивов данных можно получить с помощью инструмента анализа данных Описательная статистика. Порядок действий следующий:
1. Необходимо проверить доступ к Пакету анализа. Для этого в главном меню нужно выбрать Сервис / Настройки и напротив Пакета анализа установить флажок.
2. Выбрать в главном меню Сервис / Анализ данных / Описательная статистика и заполнить диалоговое окно (рис. 2.3):

Рис. 2.3. Диалоговое окно ввода параметров инструмента
Описательная статистика
Входной интервал – диапазон, содержащий данные результативного и объясняющих признаков;
Группирование – указать, как расположены данные (в столбцах или строках);
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист – можно задать произвольное имя нового листа, на который будут выведены результаты.
Для получения информации Итоговой статистики, Уровня надежности,  -го наибольшего и наименьшего значений нужно установить соответствующие флажки в диалоговом окне.
-го наибольшего и наименьшего значений нужно установить соответствующие флажки в диалоговом окне.
Получаем следующую статистику (рис. 2.4):

Рис. 2.4. Результат применения инструмента Описательная статистика
Выборочные ковариации и дисперсии можно найти несколькими способами:
1 способ) Выборочные ковариации находятся с помощью статистической функции КОВАР(диапазон1;диапазон2), а выборочные дисперсии – с помощью ДИСПР(диапазон).
2 способ) Матрицу коэффициентов выборочных дисперсий и ковариаций можно получить с помощью инструмента анализа данных Ковариация. Для этого необходимо выбрать в главном меню Сервис / Анализ данных / Ковариация и заполнить диалоговое окно (рис. 2.5):

Рис. 2.5. Диалоговое окно ввода параметров инструмента Ковариация
В результате получаем следующие данные (рис. 2.6):

Рис. 2.6. Результат применения инструмента Ковариация
Из рис. 2.6 видно, что выборочная ковариация между  и
и  равна 219,315; между
равна 219,315; между  и
и  – 345,5; между
– 345,5; между  и
и  – 8515,79. Выборочная дисперсия
– 8515,79. Выборочная дисперсия  равна 9,37;
равна 9,37;  – 6558,078;
– 6558,078;  – 13838,89.
– 13838,89.
Для проверки наличия коллинеарности или мультиколлинеарности и отбора факторов с помощью инструмента анализа данных Корреляция можно получить матрицу парных коэффициентов корреляции. Для этого необходимо выбрать в главном меню Сервис / Анализ данных / Корреляция и заполнить диалоговое окно (рис. 2.7):

Рис. 2.7. Диалоговое окно ввода параметров инструмента Корреляция
Получаем следующую матрицу коэффициентов парной корреляции (рис. 2.8), которые совпадают с вычисленными ранее.

Рис. 2.8. Матрица коэффициентов парной корреляции
Между факторами наблюдается мультиколлинеарность, так как значения всех коэффициентов корреляции больше 0,7.
Для вычисления параметров линейного уравнения множественной регрессии также как при вычислении параметров линейного уравнения парной регрессии используется инструмент анализа данных Регрессия, только во входном интервале Х следует указать не один столбец, а все столбцы, содержащие значения факторных признаков (рис. 2.9).

Рис. 2.9. Диалоговое окно ввода параметров инструмента Регрессия
Результаты анализа представлены на рис. 2.10.



Рис. 2.10. Результат применения инструмента Регрессия
Следовательно, множественный коэффициент корреляции равен 0,96; множественный коэффициент детерминации 0,93; скорректированный коэффициент детерминации 0,918. На уровне значимости 0,05 фактическое значение 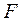 -критерия Фишера 79,62. Уравнение множественной линейной регрессии имеет вид:
-критерия Фишера 79,62. Уравнение множественной линейной регрессии имеет вид:  =-13,02+29,83
=-13,02+29,83  +0,3
+0,3 
Из рис. 2.10, на котором получены графики остатков  и
и  видим, что расположение остатков не имеет направленности. Следовательно, они независимы от значений
видим, что расположение остатков не имеет направленности. Следовательно, они независимы от значений  значит построенная модель адекватна.
значит построенная модель адекватна.
Пример 2.2. По данным табл. 1.1 проверить наличие гетероскедастичности остатков.
Решение:
1 способ) графический. В примере 1.1 было получено уравнение парной линейной регрессии  =-17,78+36,87
=-17,78+36,87  вычислены теоретические значения
вычислены теоретические значения  и остатки
и остатки 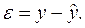 Эти результаты можно получить намного проще, используя регрессионный анализ. Для этого в диалоговом окне ввода параметров инструмента Регрессия нужно поставить флажок напротив «Остатки» и в Excel дополнительно будет выведены сведения, как на рис. 2.11.
Эти результаты можно получить намного проще, используя регрессионный анализ. Для этого в диалоговом окне ввода параметров инструмента Регрессия нужно поставить флажок напротив «Остатки» и в Excel дополнительно будет выведены сведения, как на рис. 2.11.
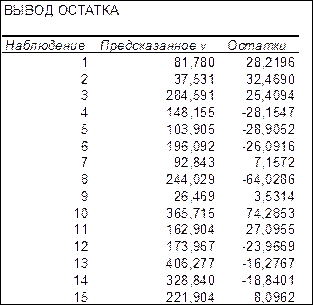
Рис. 2.11. Результат применения инструмента Регрессия (вывод остатка)
Предсказанное  – это теоретические значения
– это теоретические значения 
Таким образом, во вспомогательных таблицах можно не рассчитывать столбцы  и
и  а использовать результаты регрессионного анализа.
а использовать результаты регрессионного анализа.
По данным рис. 2.11 построим график остатков (рис. 2.12). Остаточные величины  не обнаруживают тенденцию по мере увеличения
не обнаруживают тенденцию по мере увеличения  и
и  Следовательно, есть равенство дисперсий остаточных величин, т.е. не наблюдается гетероскедастичности остатков.
Следовательно, есть равенство дисперсий остаточных величин, т.е. не наблюдается гетероскедастичности остатков.

Рис. 2.12. График остатков
2 способ) теоретический. Для применения теста Гольдфельда-Квандта упорядочим данные по фактору 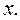 Исключим из рассмотрения
Исключим из рассмотрения  =5 центральных наблюдений. Разделим оставшуюся совокупность из 15-5=10 наблюдений на две группы (по 5) и определим по каждой из групп уравнение регрессии. Это легко сделать, используя результаты регрессионного анализа (в главном меню выбрать Сервис / Анализ данных / Регрессия и установить флажок напротив «Остатки»). Результаты расчетов сведем в табл. 2.3, вычислив
=5 центральных наблюдений. Разделим оставшуюся совокупность из 15-5=10 наблюдений на две группы (по 5) и определим по каждой из групп уравнение регрессии. Это легко сделать, используя результаты регрессионного анализа (в главном меню выбрать Сервис / Анализ данных / Регрессия и установить флажок напротив «Остатки»). Результаты расчетов сведем в табл. 2.3, вычислив  и суммы по каждой группе.
и суммы по каждой группе.
Таблица 2.3
| Уравнения регрессии | 
| 
| 
| 
| 
|
Первая группа с первыми 5 наблюдениями:  =20,31+24,23 =20,31+24,23 
| 1,2 | 49,38 | -19,38 | 375,640 | |
| 1,5 | 56,65 | 13,35 | 178,236 | ||
| 2,7 | 85,72 | 24,28 | 589,438 | ||
| 3,0 | 92,99 | 7,01 | 49,144 | ||
| 3,3 | 100,26 | -25,26 | 637,953 | ||
Сумма 
| 1830,412 | ||||
Вторая группа с последними 5 наблюдениями:  =-138,46+49,83 =-138,46+49,83 
| 7,1 | 215,37 | -35,37 | 1250,803 | |
| 8,2 | 270,19 | 39,81 | 1585,234 | ||
| 9,4 | 329,99 | -19,99 | 399,472 | ||
| 10,4 | 379,82 | 60,18 | 3621,439 | ||
| 11,5 | 434,64 | -44,64 | 1992,721 | ||
Сумма 
| 8849,670 |
Величина  =
= 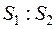 =8849,670:1830,412=4,83
=8849,670:1830,412=4,83 
 =9,28 при 5%-ном уровне значимости и числе степеней свободы
=9,28 при 5%-ном уровне значимости и числе степеней свободы  =
=  =(15-5-2·2):2=3.
=(15-5-2·2):2=3.
Так как  то гетероскедастичность остатков отсутствует.
то гетероскедастичность остатков отсутствует.
IIi. временные ряды
1. Основные определения и формулы
При построении эконометрической модели используются два типа данных:
1) данные, характеризующие совокупность различных объектов в определенный момент времени (пространственные модели);
2) данные, характеризующие один объект за ряд последовательных моментов времени (модели временных рядов).
Временной ряд (ряд динамики) – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется из трендовой  циклической
циклической  и случайной
и случайной  компонент.
компонент.
Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда; как произведение – мультипликативной моделью временного ряда.
Аддитивная модель: 
мультипликативная модель: 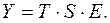
Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.
Построение аддитивной и мультипликативной моделей сводится к расчету значений 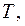
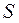 и
и  для каждого уровня ряда.
для каждого уровня ряда.
Процесс построения модели следующий:
Шаг 1. Выравнивание исходного ряда методом скользящей средней.
Шаг 2. Расчет значений сезонной компоненты 
Шаг 3. Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной  или в мультипликативной
или в мультипликативной  модели.
модели.
Шаг 4. Аналитическое выравнивание уровней  или
или  и расчет значений
и расчет значений  с использованием полученного уравнения тренда.
с использованием полученного уравнения тренда.
Шаг 5. Расчет полученных по модели значений  или
или 
Шаг 6. Расчет абсолютных и/или относительных ошибок.
Автокорреляция уровней ряда – корреляционная зависимость между последовательными уровнями временного ряда.
Коэффициент автокорреляции уровней ряда первого порядка:

где 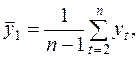

Аналогично определяются коэффициенты автокорреляции второго и более высоких порядков. Например, коэффициент автокорреляции второго порядка:
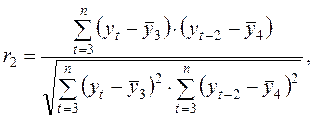
где 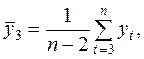

Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда, а график зависимости ее значений от величины лага (порядка коэффициента автокорреляции) – коррелограммой.
Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда.
Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения трендов чаще всего применяются линейные, гиперболические, экспоненциальные, степенные функции.
Параметры трендов определяются обычным МНК, в качестве независимой переменной выступает время  а в качестве зависимой переменной – фактические уровни временного ряда
а в качестве зависимой переменной – фактические уровни временного ряда  Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации. Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации.
Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации. Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации.
При построении моделей регрессии по временным рядам для устранения тенденции можно использовать следующие методы:
1) метод отклонений от тренда предполагает вычисление трендовых значений для каждого временного ряда модели, например  и
и  и расчет отклонений от трендов:
и расчет отклонений от трендов:  и
и  которые используют для дальнейшего анализа.
которые используют для дальнейшего анализа.
2) метод последовательных разностей заключается в следующем:
• если ряд содержит линейный тренд, то исходные данные заменяются первыми разностями: 
• если параболический тренд – вторыми разностями: 
• если экспоненциальный или степенной тренд, то этот метод применяется к логарифмам исходных данных.
Простейший подход к моделированию сезонных колебаний – это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.
Автокорреляция в остатках – корреляционная зависимость между значениями остатков  за текущий и предыдущий моменты времени.
за текущий и предыдущий моменты времени.
Для определения автокорреляции остатков используют критерий Дарбина-Уотсона:


Коэффициент автокорреляции остатков первого порядка:


Между критерием Дарбина-Уотсона и коэффициентом автокорреляции остатков первого порядка существует соотношение: 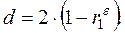
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза  об отсутствии автокорреляции остатков. Альтернативные гипотезы
об отсутствии автокорреляции остатков. Альтернативные гипотезы  и
и  состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по статистическим таблицам (таблица 3 приложения) определяются критические значения критерия Дарбина-Уотсона
состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по статистическим таблицам (таблица 3 приложения) определяются критические значения критерия Дарбина-Уотсона  и
и  для заданного числа наблюдений
для заданного числа наблюдений  числа независимых переменных модели
числа независимых переменных модели  и уровня значимости
и уровня значимости  По этим значениям числовой промежуток
По этим значениям числовой промежуток  разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью
разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью  осуществляется следующим образом:
осуществляется следующим образом:
•  – есть положительная автокорреляция остатков,
– есть положительная автокорреляция остатков,  отклоняется, с вероятностью
отклоняется, с вероятностью  принимается
принимается 
•  – зона неопределенности;
– зона неопределенности;
•  – нет оснований отклонять
– нет оснований отклонять  т.е. автокорреляция остатков отсутствует;
т.е. автокорреляция остатков отсутствует;
•  – зона неопределенности;
– зона неопределенности;
•  – есть отрицательная автокорреляция остатков,
– есть отрицательная автокорреляция остатков,  отклоняется, с вероятностью
отклоняется, с вероятностью  принимается
принимается 
Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу 
Эконометрические модели, содержащие не только текущие, но и лаговые значения факторных переменных, называются моделями с распределенным лагом, например, 
Оценка параметров моделей с распределенными лагами проводится по методу Койка или методу Алмон.
Модели, содержащие в качестве факторов лаговые значения зависимой переменной, называются моделями авторегрессии, например, 
2. Решение типовых задач
Пример 3.1. По данным табл. 2.1 требуется:
1) Рассчитать критерий Дарбина-Уотсона.
2) Оценить полученный результат при 5%-ном уровне значимости.
3) Указать, пригодно ли уравнение для прогноза.
Решение:
1) В Excel составим вспомогательную таблицу как на рис. 3.1.
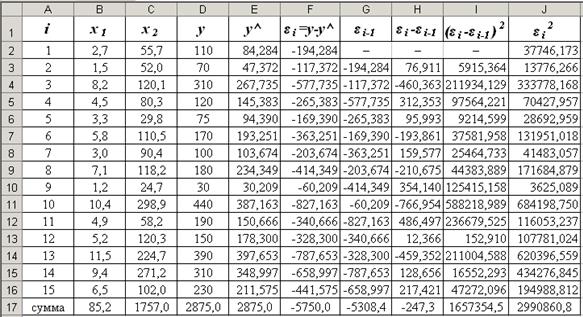
Рис. 3.1. Вспомогательная таблица к примеру 3.1
Теоретические значения  можно определить несколькими способами:
можно определить несколькими способами:
1 способ) Используя полученное в примере 2.1 уравнение множественной линейной регрессии  =-13,02+29,83
=-13,02+29,83  +0,3
+0,3  можно вычислить для каждого набора
можно вычислить для каждого набора  и
и  свое значение
свое значение 
2 способ) Применить инструмент анализа данных Регрессия (Сервис / Анализ данных), поставив флажок для вывода остатков. В столбце с названием «Предсказанное  » будут находиться теоретические значения
» будут находиться теоретические значения 
Заполним столбец G, который получается смещением столбца F на одно значение вниз. Столбец H найдем как разность между столбцами F и G. Заполним столбцы I и J, возведя в квадрат значения столбцов F и H соответственно.
Критерий Дарбина-Уотсона рассчитываем по формуле:
 или в Excel =I17/J17.
или в Excel =I17/J17.
2) Фактическое (найденное выше) значение сравним с табличными значениями при 5%-ном уровне значимости. При  =15 и
=15 и  =2 нижнее значение
=2 нижнее значение  =0,95, а верхнее
=0,95, а верхнее  =1,54 (таблица 3 приложения). Так как
=1,54 (таблица 3 приложения). Так как  то это означает наличие в остатках положительной автокорреляции.
то это означает наличие в остатках положительной автокорреляции.
3) Уравнение регрессии не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь разные причины. Автокорреляция в остатках может означать, что в уравнение не включен какой-либо существенный фактор; возможно, что форма связи неточна или в рядах динамики имеется общая тенденция.
3. Решение задач помощью электронных таблиц Excel
Пример 3.2. Динамика объема платных услуг населению региона по кварталам 2004-2007 гг. характеризуется данными, представленными в табл. 3.1.
Таблица 3.1
| Год | Квартал | 
| Объем платных услуг населению (млн. руб.), 
|
| I | |||
| II | |||
| III | |||
| IV | |||
| I | |||
| II | |||
| III | |||
| IV | |||
| I | |||
| II | |||
| III | |||
| IV | |||
| I | |||
| II | |||
| III | |||
| IV |
Необходимо построить аддитивную модель временного ряда, оценить качество построенной модели и сделать прогноз об объеме платных услуг населению на I и II кварталы 2008 г.
Решение:
Занесем данные  и
и  в Excel и построим поле корреляции (рис. 3.2):
в Excel и построим поле корреляции (рис. 3.2):

Рис. 3.2. Корреляционное поле
Рассчитаем коэффициенты автокорреляции. Для этого составляем первую вспомогательную таблицу 3.2.
Таблица 3.2
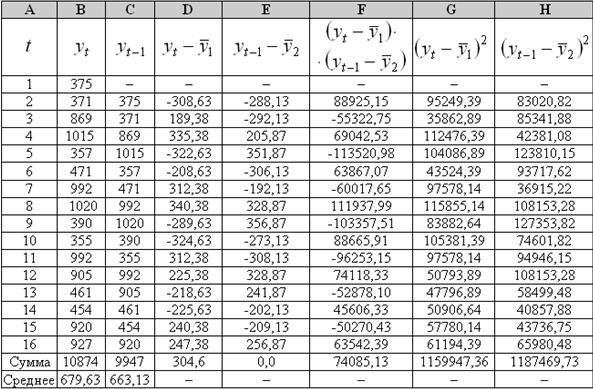
Столбец С получается сдвигом данных столбца B на одно значение вниз. Столбец D вычисляется как разность между столбцом B и его средним значением (679,63).
Замечание. Для вычисления средних используйте статистическую функцию СРЗНАЧ(диапазон), поскольку среднее значение  получается путем деления суммы не на 16, а на 15.
получается путем деления суммы не на 16, а на 15.
Например, в ячейке I5 вычислим коэффициент автокорреляции первого порядка: = F18/КОРЕНЬ(G18*H18) или

Аналогично составляем вспомогательную таблицу для расчета коэффициента автокорреляции второго порядка. Для этого скопируем табл. 3.2 и вставим ее ниже (например, начиная с ячейки A21), а затем немного исправим значения. В результате получим табл. 3.3.
Таблица 3.3

Следовательно,

Аналогично находим коэффициенты автокорреляции более высоких порядков, и все полученные значения заносим в сводную табл. 3.4, на основании которой построим коррелограмму (рис. 3.3).
Таблица 3.4
| Лаг | 
|
| 0,063125 | |
| -0,957281 | |
| -0,037521 | |
| 0,964635 | |
| 0,046429 | |
| -0,973828 | |
| -0,073964 | |
| 0,961077 | |
| 0,146166 | |
| -0,972632 | |
| -0,114039 | |
| 0,983594 | |
| 0,241605 | |
| -0,999972 |

Рис. 3.3. Коррелограмма
Анализ коррелограммы (рис. 3.3) и графика (рис. 3.2) исходных уровней временного ряда позволяет сделать вывод о наличии в изучаемом временном ряде сезонных колебаний периодичностью в четыре квартала.
Таким образом, данный временной ряд содержит сезонные колебания периодичностью 4, т.к. объем платных услуг населению в первый-второй кварталы ниже, чем в третий-четвертый.
Рассчитаем компоненты аддитивной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого заполним табл. 3.5:
• Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы платных услуг населению (столбец C). Для этого в ячейку C3 поместим = СУММ(B2:B5) и протянем за правый нижний уголок ячейки до ячейки C15. В результате произойдет автоматическое заполнение диапазона C3 – C15.
• Разделив полученные суммы на 4, найдем скользящие средние (столбец D). Например, в ячейку D3 поместим = C3/4. Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
• Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (столбец E). Например, в ячейку E4 поместим = СРЗНАЧ(D3:D4).
Таблица 3.5
| A | B | C | D | E | F | |

| 
| Итого за четыре квартала | Скользящая средняя за четыре квартала | Центрированная скользящая средняя | Оценка сезонной компоненты | |
| – | – | – | – | |||
| 657,50 | – | – | ||||
| 653,00 | 655,250 | 213,750 | ||||
| 678,00 | 665,500 | 349,500 | ||||
| 708,75 | 693,375 | -336,375 | ||||
| 710,00 | 709,375 | -238,375 | ||||
| 718,25 | 714,125 | 277,875 | ||||
| 689,25 | 703,750 | 316,250 | ||||
| 689,25 | 689,250 | -299,250 | ||||
| 660,50 | 674,875 | -319,875 | ||||
| 678,25 | 669,375 | 322,625 | ||||
| 703,00 | 690,625 | 214,375 | ||||
| 685,00 | 694,000 | -233,000 | ||||
| 690,50 | 687,750 | -233,750 | ||||
| – | – | – | – | |||
| – | – | – | – |
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (столбец F табл. 3.5). Так, в ячейку F4 поместим = B4-E4.
Составим таблицу 3.6, распределив значения столбца F таблицы 3.5 по кварталам и годам. С помощью статистической функции СРЗНАЧ(диапазон) найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты 
В ячейке G25 рассчитаем сумму средних с помощью встроенной статистической функции = СУММ(C25:F25).
Вычислим корректирующий коэффициент:  11,25/4=2,8125. Рассчитаем скорректированные значения сезонной компоненты
11,25/4=2,8125. Рассчитаем скорректированные значения сезонной компоненты  и занесем полученные данные в табл. 3.6.
и занесем полученные данные в табл. 3.6.
В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю (ячейка G26).
Таблица 3.6
| A | B | C | D | E | F | G | |
| Показатели | Год | № квартала, 
| Сумма | ||||
| I | II | III | IV | ||||
| – | – | 213,750 | 349,500 | ||||
| -336,375 | -238,375 | 277,875 | 316,250 | ||||
| -299,250 | -319,875 | 322,625 | 214,375 | ||||
| -233,000 | -233,750 | – | – | ||||

| -289,542 | -264,000 | 271,417 | 293,375 | 11,25 | ||

| -292,354 | -266,813 | 268,604 | 290,563 | 0,0 |
Составим табл. 3.7, в которой в столбец С поместим вычисленные  . Причем через каждые четыре квартала эти значения будут повторяться.
. Причем через каждые четыре квартала эти значения будут повторяться.
Таблица 3.7
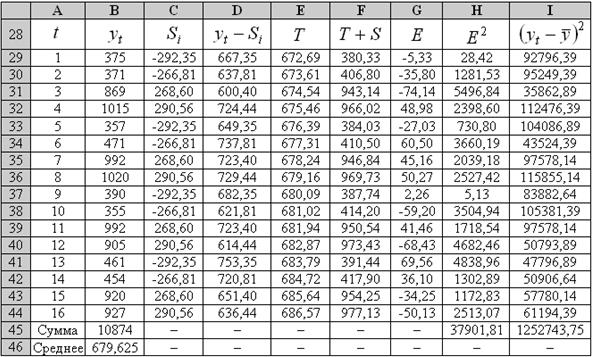
Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. В столбце D табл. 3.7 получим величины  которые рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
которые рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту  данной модели аналитическим выравниванием ряда
данной модели аналитическим выравниванием ряда  с помощью линейного тренда. Порядок действий:
с помощью линейного тренда. Порядок действий:
• Выделим диапазон значений D29:D44, а затем в главном меню выберем Вставка / Диаграмма и, следуя рекомендациям Мастера Диаграмм, построим График с маркерами, помечающими точки данных.
• На полученной диаграмме выделим Область построения диаграммы и в главном меню выберем Диаграмма / Добавить линию тренда. В диалогом окне на вкладке Тип выберем Линейная, а на вкладке Параметры поставим флажок «показать уравнение на диаграмме». Получим рис. 3.4:
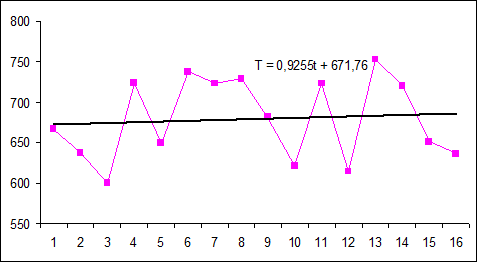
Рис. 3.4. Линейный тренд аддитивной модели
В результате аналитического выравнивания линейный тренд имеет вид:  =671,76+0,9255
=671,76+0,9255  Подставляя в это уравнение значения
Подставляя в это уравнение значения  =1,2, …, 16, найдем уровни
=1,2, …, 16, найдем уровни  для каждого момента времени (столбец E табл. 3.7).
для каждого момента времени (столбец E табл. 3.7).
Шаг 5. Найдем значения уровней ряда. Для этого прибавим к уровням  значения сезонной компоненты для соответствующих кварталов (столбец F табл. 3.7). Например, F29 =C29+E29.
значения сезонной компоненты для соответствующих кварталов (столбец F табл. 3.7). Например, F29 =C29+E29.
На одном графике (рис. 3.5) построим фактические значения уровней временного ряда  и теоретические
и теоретические  полученные по аддитивной модели.
полученные по аддитивной модели.

Рис. 3.5. Фактические и теоретические значения уровней
временного ряда, полученные по аддитивной модели
Вычислим абсолютные ошибки (столбец G табл. 3.7):  Например, в ячейку G29 поместим = B29-F29. В столбце H найдем
Например, в ячейку G29 поместим = B29-F29. В столбце H найдем 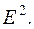
Для оценки качества построенной модели вычислим:

Следовательно, аддитивная модель объясняет 97% общей вариации уровней временного ряда объема платных услуг населению по кварталам за 4 года.
Шаг 6. Прогнозирование по аддитивной модели. Прогнозное значение уровня временного ряда в аддитивной модели  Для определения
Для определения  воспользуемся уравнением тренда
воспользуемся уравнением тренда  =671,76+0,9255
=671,76+0,9255  Получим:
Получим:
 =671,76+0,9255·17=687,494;
=671,76+0,9255·17=687,494;  =671,76+0,9255·18=688,419.
=671,76+0,9255·18=688,419.
Значения сезонных компонент за соответствующие кварталы: 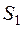 =-292,35 и
=-292,35 и  =-266,81. Значит,
=-266,81. Значит,  395,14 и
395,14 и  421,61.
421,61.
Т.е. в первые два квартала 2008 г. следовало ожидать предоставления объема платных услуг населению на 395,14 и 421,61 млн. руб. соответственно.
Пример 3.3. По данным табл. 3.1 построить мультипликативную модель временного ряда, оценить качество построенной модели и сделать прогноз об объеме платных услуг населению на I и II кварталы 2008 г.
Решение:
Шаг 1. Полностью совпадает с методикой построения аддитивной модели. Можно скопировать табл. 3.5 без столбца F на новый лист Excel (табл. 3.8).
Таблица 3.8
| A | B | C | D | E | F | |

| 
| Итого за четыре квартала | Скользящая средняя за четыре квартала | Центрированная скользящая средняя | Оценка сезонной компоненты | |
| – | – | – | – | |||
| 657,50 | – | – | ||||
| 653,00 | 655,250 | 1,326 | ||||
| 678,00 | 665,500 | 1,525 | ||||
| 708,75 | 693,375 | 0,515 | ||||
| 710,00 | 709,375 | 0,664 | ||||
| 718,25 | 714,125 | 1,389 | ||||
| 689,25 | 703,750 | 1,449 | ||||
| 689,25 | 689,250 | 0,566 | ||||
| 660,50 | 674,875 | 0,526 | ||||
| 678,25 | 669,375 | 1,482 | ||||
| 703,00 | 690,625 | 1,310 | ||||
| 685,00 | 694,000 | 0,664 | ||||
| 690,50 | 687,750 | 0,660 | ||||
| – | – | – | – | |||
| – | – | – | – |
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (столбец F табл. 3.8). Например, в ячейку F4 поместим = B4/E4.
Составим табл. 3.9, распределив значения столбца F таблицы 3.8 по кварталам и годам. С помощью статистической функции СРЗНАЧ(диапазон) найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты  В ячейке G25 рассчитаем сумму средних с помощью статистической функции = СУММ(C25:F25).
В ячейке G25 рассчитаем сумму средних с помощью статистической функции = СУММ(C25:F25).
Таблица 3.9
| A | B | C | D | E | F | G | |
| Показатели | Год | № квартала, 
| Сумма | ||||
| I | II | III | IV | ||||
| – | – | 1,326 | 1,525 | ||||
| 0,515 | 0,664 | 1,389 | 1,449 | ||||
| 0,566 | 0,526 | 1,482 | 1,310 | ||||
| 0,664 | 0,660 | – | – | ||||

| 0,582 | 0,617 | 1,399 | 1,428 | 4,026 | ||

| 0,578 | 0,613 | 1,390 | 1,419 | 4,0 |
Вычислим корректирующий коэффициент:  4/4,026=0,9936. Рассчитаем скорректированные значения сезонной компоненты
4/4,026=0,9936. Рассчитаем скорректированные значения сезонной компоненты  и занесем полученные данные в табл. 3.9.
и занесем полученные данные в табл. 3.9.
Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4, как и сумма  в ячейке G26.
в ячейке G26.
Составим табл. 3.10, в которой в столбец С поместим вычисленные  . Причем через каждые четыре квартала эти значения будут повторяться.
. Причем через каждые четыре квартала эти значения будут повторяться.
Таблица 3.10

Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате в столбце D табл. 3.10 получим величины  которые содержат только тенденцию и случайную компоненту.
которые содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту  в мультипликативной модели выравниванием ряда
в мультипликативной модели выравниванием ряда  с помощью линейного тренда. Порядок действий:
с помощью линейного тренда. Порядок действий:
• Выделим диапазон значений D29:D44, а затем в главном меню выберем Вставка / Диаграмма и, следуя рекомендациям Мастера Диаграмм, построим График с маркерами, помечающими точки данных.
• На полученной диаграмме выделим Область построения диаграммы и в главном меню выберем Диаграмма / Добавить линию тренда. В диалогом окне на вкладке Тип выберем Линейная, а на вкладке Параметры поставим флажок «показать уравнение на диаграмме». Получим рис. 3.6:

Рис. 3.6. Линейный тренд мультипликативной модели
В результате аналитического выравнивания линейный тренд имеет вид:  =651,63+3,2813
=651,63+3,2813  Подставляя в это уравнение значения
Подставляя в это уравнение значения  =1,2, …, 16, найдем уровни
=1,2, …, 16, найдем уровни  для каждого момента времени (столбец E табл. 3.10).
для каждого момента времени (столбец E табл. 3.10).
Шаг 5. Найдем уровни ряда, умножив значения  на соответствующие значения сезонной компоненты (столбец F табл. 3.10). Например, в ячейку F29 поместим = C29*E29.
на соответствующие значения сезонной компоненты (столбец F табл. 3.10). Например, в ячейку F29 поместим = C29*E29.
На одном графике (рис. 3.7) построим фактические значения уровней временного ряда  и теоретические
и теоретические 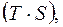 полученные по мультипликативной модели.
полученные по мультипликативной модели.
Вычислим абсолютные ошибки (столбец G табл. 3.10):  Например, в ячейку G29 поместим = B29/F29.
Например, в ячейку G29 поместим = B29/F29.
В столбце H найдем 
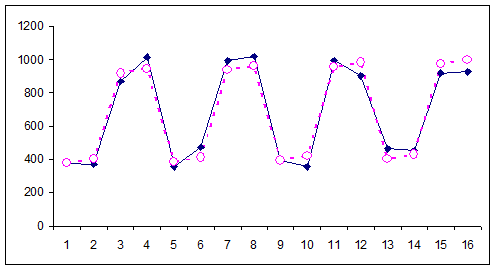
Рис. 3.7. Фактические и теоретические значения уровней
временного ряда, полученные по мультипликативной модели
Для оценки качества построенной мультипликативной модели вычислим:

Следовательно, мультипликативная модель объясняет 96,6% общей вариации уровней временного ряда объема платных услуг населению по кварталам за 4 года.
Сравнивая показатели детерминации аддитивной и мультипликативной моделей, делаем вывод, что они примерно одинаково аппроксимируют исходные данные.
Шаг 6. Прогнозирование по мультипликативной модели. Прогнозное значение  уровня временного ряда в мультипликативной модели есть произведение трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда
уровня временного ряда в мультипликативной модели есть произведение трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда  =651,63+3,2813
=651,63+3,2813  Получим:
Получим:
 =651,63+3,2813·17=707,412;
=651,63+3,2813·17=707,412;
 =651,63+3,2813·18=710,693.
=651,63+3,2813·18=710,693.
Значения сезонных компонент за соответствующие кварталы равны: 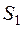 =0,578 и
=0,578 и  =0,613. Таким образом,
=0,613. Таким образом,
 =408,84;
=408,84;
 =435,48.
=435,48.
Т.е. в первые два квартала 2008 г. следовало ожидать предоставления объема платных услуг населению на 408,84 и 435,48 млн. руб. соответственно.
Таким образом, аддитивная и мультипликативная модели дают примерно одинаковый результат по прогнозу.
библиографический список
1. Гладилин А.В. Эконометрика: Учебное пособие / А.В. Гладилин, А.Н. Герасимов, Е.И. Громов. – М.: КНОРУС, 2006. – 232 с.
2. Доугерти К. Введение в эконометрику. – М.: ИНФРА-М, 2001. – 402 с.
3. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.:ЮНИТИ-ДАНА, 2006. – 311 с.
4. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика: Начальный курс: Учеб. – М.: Дело, 2001. – 400 с.
5. Орлов А.И. Эконометрика. Учебник. – М.: Экзамен, 2002. – 576 с.
6. Практикум по эконометрике / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2005. – 192 с.
7. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2006. – 576 с.
8. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. – М.: ЮНИТИ, 1998. – 1022 с.
приложения.
статистические таблицы
1. Таблица значений 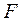 -критерия Фишера при уровне значимости
-критерия Фишера при уровне значимости 


| 
| |||||||||
| 161,5 | 199,5 | 215,7 | 224,6 | 230,2 | 233,9 | 238,9 | 243,9 | 249,0 | 254,3 | |
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 | |
| 6,61 |
Date: 2016-06-09; view: 1143; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |