
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Защита контрольно-курсовой работы
Защита ККР проводится преподавателю, который ее консультировал. При этом студенту могут быть заданы вопросы по тематике ККР с целью контроля самостоятельности ее выполнения. За защиту ККР студент может получить до 20 баллов за выполнение всех заданий работы и правильные ответы на вопросы при защите работы, при неправильных ответах оценка снижается на 5 балла за каждое задание работы, по которому был дан неверный ответ. Студенты, не выполнившие, или не защитившие контрольно-курсовую работу не допускаются к зачету. Защита работы может проходить в форме тестирования;
4. Методические указания к работе над контрольно-курсовой работой
Ниже приведен пример выполнения контрольно-курсовой работы для приведенного в настоящем методическом пособии варианта.
1. Первое задание. Вычисления в различных системах счисления:
В любой позиционной системе число, состоящее из K цифр –  можно разложить по степеням некоторого числа a, которое называется основанием системы счисления:
можно разложить по степеням некоторого числа a, которое называется основанием системы счисления:

Например, в двоичной системе счисления:
10a= 1× a1 +0× a0 = a
Легко показать, что в любой системе счисления число 10 равно основанию системы счисления а.
Двоичная система счисления не всегда хорошо читается человеком, поэтому при кодировании двоичные числа часто представляют шестнадцатеричными или восьмеричными числами, для которых возможен прямой перевод в двоичную систему счисления по тетрадам (четверкам) для шестнадцатеричной или триадам (тройкам) для восьмеричной системы счисления. Перевод шестнадцатеричных цифр в двоичные числа приведен в таблице.
| Десятичные числа | Шестнадцатеричные цифры | Двоичные числа (тетрады) | Двоичные числа (триады) | Восьмеричные цифры | Двоично-десятичные числа |
| 0 | 0 | 0000 | 000 | 0 | 0000 |
| 1 | 1 | 0001 | 001 | 1 | 0001 |
| 2 | 2 | 0010 | 010 | 2 | 0010 |
| 3 | 3 | 0011 | 011 | 3 | 0011 |
| 4 | 4 | 0100 | 100 | 4 | 0100 |
| 5 | 5 | 0101 | 101 | 5 | 0101 |
| 6 | 6 | 0110 | 110 | 6 | 0110 |
| 7 | 7 | 0111 | 111 | 7 | 0111 |
| 8 | 8 | 1000 | 1000 | ||
| 9 | 9 | 1001 | 1001 | ||
| 10 | A | 1010 | 0001 0000 | ||
| 11 | B | 1011 | 0001 0001 | ||
| 12 | C | 1100 | 0001 0010 | ||
| 13 | D | 1101 | 0001 0011 | ||
| 14 | E | 1110 | 0001 0100 | ||
| 15 | F | 1111 | 0001 0101 |
Вычисления целесообразно начать с шестнадцатеричной системы, например
ВD+19
Результат вычислений удобно представить в виде столбца:
| 1 | ||
| B | D | |
| + | 1 | 9 |
| D | 6 |
В крайнем правом столбце в результате вычисления получаем:
D + 9 = 1310 + 9 = 22, поскольку 22>15, требуется перенос в старший разряд
22 = 1610 + 6 =1616
С учетом переноса в левом столбце получаем:
B + 1 + 1 = D
Выполним вычисления в двоичной системе счисления. Для этого переведем шестнадцатеричные цифры в двоичные тетрады согласно приведенной выше таблицы, а затем из тетрад сформируем двоичные числа. Такой прямой поразрядный перевод из шестнадцатеричной системы счисления в двоичную возможен, поскольку основания этих систем счисления находятся в степенной зависимости. Получим:ем счисления находят руем двоичные числа. Такой прямой поразрядный перевод из шестнадцатеричной сис
В= 10112
D= 11012
1 = 00012
9 = 10012
ВD= 1011 11012
1916=0001 10012
Выполним сложение, учитывая, что
0+0= 0
1+0= 1
1+1 =102
1+1+1 =112
В результате с учетом переносов в старшие разряды получим:
| 1 | 1 | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | |
| + | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
Выполнив обратный перевод результата в шестнадцатеричную систему счисления (по тетрадам) можно убедиться в его правильности:
11012 = D
01102 = 6
1101 01102 = D6
Выполним вычисления в восьмеричной системе счисления. Перевод в восьмеричную систему счисления удобно выполнять из двоичной системы счисления, разбивая число на триады, начиная с младших разрядов (справа).
ВD= 1011 11012 = 010 111 1012
Из таблицы получаем:
0102 = 2
1112 = 7
1012 = 5
ВD = 2758
Аналогично получим:
1916=0001 10012 = 000 011 0012
0002 = 0
0112 = 3
0012 = 1
1916 = 318
Осуществим поразрядное сложение 2758 + 318
В результате получим:
| 1 | |||
| 2 | 7 | 5 | |
| + | 3 | 1 | |
| 3 | 2 | 6 |
Вычисления выполняются аналогично шестнадцатеричной системе
5 + 1 = 68
7 + 3 = 1010 , поскольку 10>7 требуется перенос в старший разряд
1010 = 810 + 2 = 128
2 + 1 = 38
Таким образом:
2758 + 318 = 3268
Выполним проверку путем перевода результата в двоичную и шестнадцатеричную системы счисления
38 = 0112
28 = 0102
68 = 1102
Отсюда получим
3268 = 011 010 1102 = 1101 01102 = D616
Произведем вычисления в десятичной системе счисления. Перевод в десятичную систему счисления возможен из любой рассмотренной выше системы счисления, однако удобнее производить этот перевод из шестнадцатеричной системы.
ВD= В× 161+D× 160=1110×16+1310=18910
1916= 1× 161+9× 160=2510
18910+2510=21410
21410=1310×16+6 =D6
Таким образом, результаты вычислений во всех системах счисления совпали.
2. Пример выполнения задания на минимизацию методом S-кубов.
Пусть некоторая логическая функция задана следующей таблицей соответствия:
| X 0 | X 1 | X 2 | X 3 | X 4 | X 5 | X 6 | X 7 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| y |
Здесь  аргументы функции, а
аргументы функции, а  входные слова – наборы значений аргументов. Например,
входные слова – наборы значений аргументов. Например,  .
.
На основе данной таблицы можно получить аналитическое выражение для логической функции в совершенной дизъюнктивной или конъюнктивной нормальной формах (СДНФ или СКНФ). Элементы СДНФ называют минитермами, а СКНФ – макстермами. СДНФ представляет собой дизъюнкцию минитермов, а СКНФ – конъюнкцию макстермов. В свою очередь, минитерм представляет собой конъюнкцию переменных или их инверсий (напрмер  ), а макстерм – дизъюнкцию (например,
), а макстерм – дизъюнкцию (например,  ). Легко обнаружить, что минитерм равен 1 только при одном единственном входном слове, а макстерм равен 0 также только при одном единственном входном слове. По отношению к этим словам минитерм называют конституентой единицы, а макстерм – конституентой нуля. Тогда аналитическое выражение функции в форме СДНФ будет содержать конституенты единиц (и только их) для входных слов, при которых функция =1, а в форме СКНФ будет содержать конституенты нулей (и только их) для входных слов, при которых функция =0. При этом, если аргумент во входном слове =1, он входит в конституенту единицы в прямой форме, а в конституенту нуля – в инверсной. И наоборот, если аргумент во входном слове =0, он входит в конституенту нуля в прямой форме, а в конституенту единицы – в инверсной.
). Легко обнаружить, что минитерм равен 1 только при одном единственном входном слове, а макстерм равен 0 также только при одном единственном входном слове. По отношению к этим словам минитерм называют конституентой единицы, а макстерм – конституентой нуля. Тогда аналитическое выражение функции в форме СДНФ будет содержать конституенты единиц (и только их) для входных слов, при которых функция =1, а в форме СКНФ будет содержать конституенты нулей (и только их) для входных слов, при которых функция =0. При этом, если аргумент во входном слове =1, он входит в конституенту единицы в прямой форме, а в конституенту нуля – в инверсной. И наоборот, если аргумент во входном слове =0, он входит в конституенту нуля в прямой форме, а в конституенту единицы – в инверсной.
В результате для заданной функции можно получить следующие аналитические выражения в форме СДНФ

и СКНФ

Таким образом, любая булева функция представима в совершенной нормальной форме (дизъюнктивной или конъюнктивной). Такое представление является первым шагом перехода от табличного задания функции к ее аналитическому выражению.
Каноническая задача синтеза логических схем сводится к минимизации булевых функций, т. е. к представлению их в дизъюнктивной нормальной форме, которая содержит наименьшее число букв (переменных и их отрицаний). Такие формы называют минимальными. Формула, представленная в дизъюнктивной нормальной форме, упрощается многократным применением закона склеивания  и закона поглощения
и закона поглощения 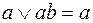 . Здесь под a и b можно понимать любую формулу алгебры логики. Однако при применении закона склеивания возникает проблема, что с чем склеивать, так как легко можно получить тупиковую форму, которая не будет минимальной, но не будет также и упрощаться. Поэтому для минимизации логических функций используют графо-аналитические методы, одним из которых является метод S-кубов.
. Здесь под a и b можно понимать любую формулу алгебры логики. Однако при применении закона склеивания возникает проблема, что с чем склеивать, так как легко можно получить тупиковую форму, которая не будет минимальной, но не будет также и упрощаться. Поэтому для минимизации логических функций используют графо-аналитические методы, одним из которых является метод S-кубов.
Отобразим логическую функцию в логическом пространстве (Рисунок 1). Легко обнаружить, что данная логическая функция будут задана только в вершинах куба с длиной ребра, равной 1. Отметим (зачерним) все вершины (точки в логическом пространстве), в которых функция равна 1.
Для каждой вершины можно записать соответствующую ей конституенту единицы (рисунок 2). Легко обнаружить, что к конституентам единиц для точек, принадлежащих одному ребру можно применить закон склеивания. Тогда для ребер появятся новые конституенты, содержащие уже только две переменные. Аналогично к подобным конституентам для двух параллельных ребер, принадлежащих одной грани, также можно применить закон склеивания и получить значения переменных или их инверсий, выступающие в качестве конституент, соответствующих граням, что показано на рисунке 1. Тогда конституенты, соответствующие ребрам могут быть получены как конъюнкции конституент граней, на пересечении которых данное ребро находится.
Теперь можно легко получить минимальную форму, как дизъюнкцию конституент (минитермов), соответствующих точкам, ребрам, граням полностью покрывающим все зачерненные точки, в которых функция равна 1 (и только их). При этом нежелательно оставлять отдельные точки, а следует склеивать их в ребра.

Рисунок 1 – Минимизация логической функции методом S-кубов.

Рисунок 2 – Другие примеры конституент единицы на S-кубе.
Из рисунка 1 видно, что все точки могут быть покрыты гранью  и ребром
и ребром  . Тогда минимальная форма для рассматриваемой функции будет иметь вид.
. Тогда минимальная форма для рассматриваемой функции будет иметь вид.
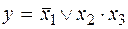
Теперь, используя графическое отображение функции можно восстановить тождественные преобразования, с помощью которых фактически была получена данная форма. Для этого, воспользовавшись выражением  , в СДНФ запишем дважды конституенту (минитерм), соответствующую точке, принадлежащей одновременно и грани и ребру (
, в СДНФ запишем дважды конституенту (минитерм), соответствующую точке, принадлежащей одновременно и грани и ребру ( ). Затем, применяя закон склеивания к точкам, принадлежащим одному ребру, а затем к параллельным ребрам получим:
). Затем, применяя закон склеивания к точкам, принадлежащим одному ребру, а затем к параллельным ребрам получим:
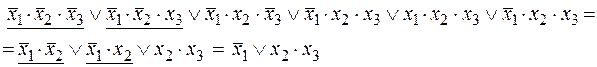
Таким образом, результат минимизации методом S-кубов проверен тождественными преобразованиями.
3. Минимизация методом карт Карно.
Методом карт Карно минимизируются функции с числом переменных до 5 – 6. Карта Карно представляет собой развертку логического пространства на плоскость (рисунок 3). Аналогично методу S-кубов на карте также можно выделить области, соответствующие переменным или их инверсиям.
Минимизируем с помощью карты Карно функцию, заданную следующей таблицей соответствия:
| X 0 | X 1 | X 2 | X 3 | X 4 | X 5 | X 6 | X 7 | X 8 | X 9 | X 10 | X 11 | X 12 | X 13 | X 14 | X 15 | |
| x1 | ||||||||||||||||
| x2 | ||||||||||||||||
| x3 | ||||||||||||||||
| x4 | ||||||||||||||||
| Y |
Отобразим данную функцию на карте Карно, проставив 1 в ячейки карты, соответствующие входным словам, при которых функция =1. Ребрам, граням и кубам на карте Карно соответствуют ортогональные области (блоки – строки, столбцы, квадраты, прямоугольники) заполненные 2, 4 и 8 единицами.

Рисунок 3 – Пример выполнения задания на минимизацию методом карт Карно.
Минитерм, соответствующий той иди иной области (блоку) определяется как конъюнкция переменных или их инверсий, соответствующих областям, на пересечении которых данная ассоциация находится. Минимальная форма формируется как дизъюнкция этих минитермов. Для приведенной функции минимальная форма будет содержать минитермы, соответствующие трем ассоциациям: из двух единиц, из четырех единиц и из 8 единиц (то есть через край карты будет полностью заполнена область  )
)
В результате минимальная форма будет иметь вид:

Второй частью третьего задания является построение логической схемы для минимальной формы. Для полученной минимальной формы логическая схема будет иметь вид, представленный на рисунке 4.

Рисунок 4 – Логическая схема для минимальной формы
4. Построение графа автомата
В четвертом задании требуется построить граф конечного автомата, заданного общей таблицей выходов и переходов (рисунок 5).
 |
| X0 | X1 | X2 | X3 | n | |||||||||
| S0 | S2/Y1 | S0/Y0 | S3/Y3 | S2/Y2 | X(n) | X1 | X2 | X2 | X0 | X1 | X3 | ||
| S1 | S3/Y7 | S2/Y3 | S2/Y5 | S1/Y1 | Y(n) | ||||||||
| S2 | S1/Y2 | S0/Y6 | S0/Y2 | S2/Y3 | S(n) | S2 | |||||||
| S3 | S1/Y0 | S0/Y2 | S0/Y0 | S3/Y4 |
Рисунок 5 – Таблицы, задающие состояния и переходы конечного автомата
В данной таблице указано, какие слова обозначают те или иные элементы таблицы. Построение графа начинается с построения четырех вершин, соответствующих четырем состояниям автомата (рисунок 6). Затем построение ведется по строкам таблицы. Например, первая строка соответствует состоянию S0. . Из соответствующей вершины для каждого входного слова X в графе проводится соответствующая дуга. Концом дуги будет вершина, соответствующая состоянию, в которое перейдет автомат в следующем такте, если на его вход подано слово X. Около каждой дуги указывается ее вес – в числителе входное слово, при котором произойдет данный переход, а в знаменателе – выходное слово, которое при этом установится. Например, при входном слове X2 из S0 на выходе установится слово Y3 и в следующем такте произойдет переход в состояние S3.
Подобное построение осуществляется для каждого исходного состояния конечного автомата (каждой строки). Пример полностью построенного графа приведен на рисунке 6.

Рисунок 6 – Граф конечного автомата.
По графу требуется осуществить моделирование работы автомата при подаче на него некоторой последовательности входных слов. Для каждого входного слова и данного состояния по графу определяется выходное слово и состояние в следующем такте S(n+1). Затем процедура повторяется для этого нового состояния и т.д. Пример моделирования работы автомата приведен ниже
| n | ||||||
| X(n) | X1 | X2 | X2 | X0 | X1 | X3 |
| Y(n) | Y6 | Y3 | Y0 | Y1 | Y6 | Y2 |
 S(n) S(n)
| S2 | S0 | S3 | S0 | S2 | S0 |
|
Date: 2016-02-19; view: 294; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |