
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Анализ конечных автоматов
Полное описание поведения автомата заключается в определении последовательности выходных сигналов при возбуждении его в тактовые моменты времени некоторой последовательностью входных сигналов. Входная и выходная последовательности представляются наборами символов (или их номеров) из алфавитов Х и У одинаковой длины l. Для такого описания, кроме характеристических функций, необходимо определить или задать начальное состояние автомата.
Наиболее удобно определять реакцию автомата на входною последовательность по его графу. Для этого достаточно проследить путь в графе, начиная от вершины начального состояния, по направлению дуг, которые отмечены очередными номерами на входной последовательности. Выходная последовательность определяется номерами, которыми отмечены дуги в порядке их следования по пройденному пути, а последовательность состоянии автомата номерами вершин, через которые проходит этот путь.
Так, из графа на рис. 28 для входной последовательности (2, 0, 1, 1, 2, 3) и начального состояния 0 имеем выходную последовательность (0, 1, 0, 0, 1, 1) и смену состояний автомата (1, 3, О, 2, 2, 3). При начальном состоянии 2 и той же входной последовательности получаем соответственно (1, 1, 0, 0, 1, 1) и (2, 3, 0, 2. 2, 3).
С помощью графа автомата легко выделить следующие характерные типы его состояний:
1) преходящее состояние, из которого можно перейти, но крайней мере, в одно другое состояние, но после этого уже нельзя возвратиться в него ни при каком воздействии (соответствующая вершина не имеет заходящих дуг, но имеет хотя бы одну исходящею дугу);
2) тупиковое состояние, в которое можно перейти, по крайней мере, из одного другого состояния, но после этого уже нельзя
выйти из него ни при каком воздействии (соответствующая вершина не имеет исходящих дуг в другие вершины, но имеет хотя бы одну входящую дугу из другой вершины);
3) изолированное состояние, из которого нельзя перейти ни в какое другое состояние и в него нельзя попасть ни из какого другого состояния (соответствующая вершина содержит только петлю).
Аналогичные определения можно дать для некоторых совокупностей состояний, рассматриваемых как подавтоматы. Если начальное состояние автомата М принадлежит непустому множеству Si состояний, которое составляет тупиковый или изолированный подавтомат, то M можно упростить исключением всех состояний, которые не принадлежат множеству Si, и всех дуг, начинающихся в этих состояниях.
Пусть М1, М2 и M3 - соответственно преходящий, тупиковый и изолированные подавтоматы автомата М, которые характеризуются множествами состояний S1, S2 и S3. Очевидно, выделение таких подавтоматов соответствует разбиению множества S состояний автомата М на непересекающиеся подмножества S1, S2 и S3,представляющие собой классы эквивалентности 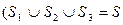 и
и  . Как следует из обобщенного графа (рис. 29), матрица соединения автомата может быть представлена в виде:
. Как следует из обобщенного графа (рис. 29), матрица соединения автомата может быть представлена в виде:
 ,
,
где  - матрицы подавтоматов М1, М2 и М3;
- матрицы подавтоматов М1, М2 и М3;  - матрица, характеризующая переходы от состояний преходящего автомата М1 к состояниям тупикового автомата М2. Отсюда следует, что разбиение автомата М на подавтоматы М1, М2 и М3 можно осуществить преобразованием его матрицы соединений к стандартному виду путем перестановки соответствующих строк и столбцов. Например, для автомата, граф которого изображен на рис. 30,
- матрица, характеризующая переходы от состояний преходящего автомата М1 к состояниям тупикового автомата М2. Отсюда следует, что разбиение автомата М на подавтоматы М1, М2 и М3 можно осуществить преобразованием его матрицы соединений к стандартному виду путем перестановки соответствующих строк и столбцов. Например, для автомата, граф которого изображен на рис. 30,
имеем:
| 3 6 2 4 7 1 5 | ||||
| М = | 0 2/0 1/0 0 | 0/1 0 1/1 0 1/0 2/1 | 0 0 0 0 | |
| 0 0 0 0 0 0 | 1/1  2/0 0 0/0
1/0 2/0 0 0/0
1/0  2/1 0/0 0
0 0/1 2/1 0/0 0
0 0/1  2/0 1/0 2/0 1/0
| 0 0 0 0 0 0 | ||
| 0 0 0 0 | 0 0 0 0 0 0 | 0/1 1/0  2/1
0/1 2/1
0/1  1/0 1/0  2/0 0 2/0 0
|
 |
Отсюда следует, что S1 = {3, 6} составляет преходящий подавтомат, S2 = {2, 4, 7} - тупиковый подавтомат и S3 = {1, 5} - изолированный подавтомат. Если начальное состояние принадлежит множеству S2, то можно упростить автомат, исключив состояния
 = {3, 6, 1, 5}, а в случае принадлежности начального состояния множеству S3 автомат упрощается исключением состояний
= {3, 6, 1, 5}, а в случае принадлежности начального состояния множеству S3 автомат упрощается исключением состояний  = {3, 6, 2, 4, 7}.
= {3, 6, 2, 4, 7}.
Синтез конечных автоматов. Реализация конечных автоматов сводится к синтезу соответствующей комбинационной схемы, преобразующей входные переменные x (v) и s (v) в выходные переменные y (v) и s (v + 1) в соответствии с заданными характеристическими функциями s (v + 1) =  (x (v), s (v)) и y (v)=
(x (v), s (v)) и y (v)= 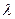 (x (v), s (v)). Для сохранения состояний s (v + 1) до следующего такта в цепь обратной связи вводится необходимое количество элементов памяти.
(x (v), s (v)). Для сохранения состояний s (v + 1) до следующего такта в цепь обратной связи вводится необходимое количество элементов памяти.
При реализации автоматов в двоичном структурном алфавите можно использовать рассмотренные ранее методы синтеза комбинационных схем. Но для этого необходимо закодировать состояния схемы н представить характеристические функции в виде булевых функций двоичных переменных. Такое кодирование можно осуществить преобразованием общей таблицы перехода автомата к таблице соответствия в двоичном структурном алфавите. Если элементы множеств X, У и S пронумерованы порядковыми числами, начиная с нуля, то им соответствуют коды, представляющие собой двоичные эквиваленты этих чисел. Например, для автомата, заданного в (4), таблицу переходов можно преобразовать к виду:
| x (v) s (v) | 0000 1111 2222 3333 0123 0123 0123 0123 |
| s (v + 1) y (v) | 3333 2220 1120 3331 0110 0000 0011 0111 |
Заменяя десятичные числа их двоичными эквивалентами, читаемыми сверху вниз, получаем таблицу соответствия, в которой значения функций s (v + 1) и у (v) представлены двоичными кодами:


| 0000 0000 1111 1111 0000 1111 0000 1111 |
| 0011 0011 0011 0011 0101 0101 0101 0101 | |


| 1111 1110 0010 1110 1111 0000 1100 1111 |
| 0110 0000 0011 0111 |


Отсюда видно, что комбинационная схема должна иметь четыре входа, соответствующие входным переменным x1 (v), х2 (v) и переменным состояния s (v), s2 (v), а также три выхода, соответствующие переменным состояния s1 (v + 1), s2 (v + 1) и выходной переменной у1 (v). Синтезировав комбинационную схему, соответствующую полученной таблице и введя два элемента задержки З1 и З2, получим структурную схему автомата (рис. 31).
Минимизация автоматов. С утилитарной точки зрения интерес представляет только зависимость между входами и выходами автомата, а роль его состоянии сводится исключительно к участию в формировании этих зависимостей в качестве промежуточных переменных. Следовательно, любая совокупность состояний, обеспечивающая требуемые зависимости между входом и выходом, может быть выбрана в качестве множества состоянии автомата. В то же время этот выбор естественно подчинить определенным целям, например, минимизации числа состояний или оптимизации автомата в каком-либо смысле. Следует иметь в виду, что с уменьшением числа состоянии уменьшается и количество требуемых элементов памяти, но это может привести к усложнению комбинационной схемы автомата. Поэтому синтез наиболее экономичного автомата часто требует поиска удачного компромисса между сложностью его комбинационной и запоминающих частей.

Рис. 32. Граф конечного автомата (а) и его сокращенная форма (б)
Минимизация числа состоянии полных автоматов связана с отношением эквивалентности. Пусть автоматы М1 и М2, находящиеся соответственно в начальных состояниях, 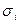 и
и  (обозначения М1 и М2 могут относиться к одному и тому же автомату), под воздействием любой входной последовательности выдают одинаковые выходные последовательности, т. е. автоматы М1 и М2 в данных состояниях
(обозначения М1 и М2 могут относиться к одному и тому же автомату), под воздействием любой входной последовательности выдают одинаковые выходные последовательности, т. е. автоматы М1 и М2 в данных состояниях 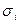 и
и  неразличимы по внешним выходам. Такое отношение между состояниями одного и того же или двух различных автоматов обладает свойствами рефлексивности, симметричности и транзитивности, следовательно, оно является отношением эквивалентности состояний. Если состояния не эквивалентны, то их называют различимыми. Легко доказать справедливость следующих положений:
неразличимы по внешним выходам. Такое отношение между состояниями одного и того же или двух различных автоматов обладает свойствами рефлексивности, симметричности и транзитивности, следовательно, оно является отношением эквивалентности состояний. Если состояния не эквивалентны, то их называют различимыми. Легко доказать справедливость следующих положений:
1) состояния 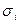 и
и  автомата явно различимы, если различаются соответствующие, им строки в таблице выходов;
автомата явно различимы, если различаются соответствующие, им строки в таблице выходов;
2) состояния 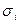 и
и  автомата явно эквививалентны, если соответствующие им строки в таблице переходов и таблице выходов одинаковы или становятся одинаковыми при замене каждого номера
автомата явно эквививалентны, если соответствующие им строки в таблице переходов и таблице выходов одинаковы или становятся одинаковыми при замене каждого номера 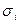 на номер
на номер  (или наоборот).
(или наоборот).
Например, для автомата, граф которого изображен на рис. 32, а, общая таблица переходов имеет вид:
| x (v) s (v) | |||
| 1/1 | 4/0 | 4/1 | |
| 5/1 | 1/1 | 4/1 | |
| 1/0 | 1/1 | 6/1 | |
| 3/1 | 2/0 | 0/1 | |
| 1/1 | 4/0 | 4/1 | |
| 1/0 | 5/1 | 4/1 | |
| 5/0 | 5/1 | 2/1 |
Из этой таблицы следует, что состояния из множества {0, 3, 4}являются явно различимыми с любым состоянием из множества {1, 2, 5, 6}. Поэтому следует искать эквивалентные состояния только среди элементов, принадлежащих одному из этих множеств. Так как строки 0 и 4 одинаковы, а строки 1 и 5 становятся одинаковыми при замене цифры в числителе 1 на 5 (или 5 на 1), то явно эквивалентными являются пары состояний {0,4} И {1,5}.
Объединяя эквивалентные состояния в автомате М1, получаем эквивалентный автомат М2 с меньшим числом состоянии, который в любом состоянии нельзя отличить от исходного, наблюдая сигналы на выходах. Очевидно, автоматы М1 и М2 являются эквивалентными, если каждому состоянию 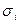 , автомата М1 соответствует, по крайней мере, одно эквивалентное ему состояние автомата M2, и если каждому состоянию
, автомата М1 соответствует, по крайней мере, одно эквивалентное ему состояние автомата M2, и если каждому состоянию  , автомата М2 соответствует хотя бы одно эквивалентное ему состояние автомата М1.
, автомата М2 соответствует хотя бы одно эквивалентное ему состояние автомата М1.
 |  |
Эквивалентные состояния, например,
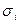 и
и  , удобно объединять по общей таблице переходов, вычеркивая строку
, удобно объединять по общей таблице переходов, вычеркивая строку  , и заменяя везде в числителе числа
, и заменяя везде в числителе числа  на
на 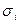 . После объединения пар явно эквивалентных состояний может оказаться возможным снова обнаружить такие состояния, которые также объединяются с помощью аналогичной процедуры. В результате последовательного объединения приходим к сокращенной таблице переходов, которой соответствует сокращенный автомат, эквивалентный исходному, но имеющий меньшее число состоянии. Так, для рассматриваемого примера получаем последовательно:
. После объединения пар явно эквивалентных состояний может оказаться возможным снова обнаружить такие состояния, которые также объединяются с помощью аналогичной процедуры. В результате последовательного объединения приходим к сокращенной таблице переходов, которой соответствует сокращенный автомат, эквивалентный исходному, но имеющий меньшее число состоянии. Так, для рассматриваемого примера получаем последовательно:
Первая таблица соответствует объединению пар эквивалентных состоянии {0,4} и {1, 5}, а вторая - объединению пары {2, 6}. Сокращенный автомат содержит только четыре состояния (рис.32, б).
Date: 2016-02-19; view: 448; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |