
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Кеңістіктегі қисық сызықты координаттар
V мен V’ аймақтары нүктелерінің арасында бір мәнді және үзіліссіз сәйкестік бар болсын. Сонымен бірге тура сәйкестік
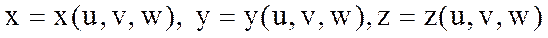 (8.10)
(8.10)
 формулаларымен анықталып, кері сәйкестік
формулаларымен анықталып, кері сәйкестік
9-сурет
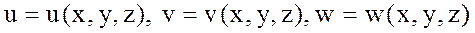 (8.11)
(8.11)
формуларымен анықталсын. (8.10) және (8.11) функцияларының өздері де, бірінші ретті дербес туындылары да үзіліссіз деп жориық. Сонда үзіліссіз якобиандар 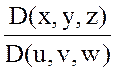 мен
мен 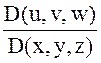 бар болады.
бар болады.
 =
= 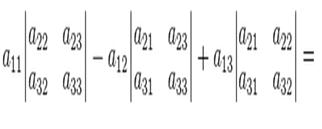
J – (8.10) функциялардың якобианы деп аталады.
2) Кеңістіктегі цилиндрлік координаттар. Декарттық координаттар жүйесінде 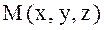 нүктесі беріліп, оның Оху жазықтығындағы проекциясы М1 нүктесі болсын. М нүктесі оның аппликатасы z және М1 өзінің полярлық кординаттары
нүктесі беріліп, оның Оху жазықтығындағы проекциясы М1 нүктесі болсын. М нүктесі оның аппликатасы z және М1 өзінің полярлық кординаттары 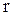 мен
мен 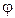 арқылы анықталса, онда
арқылы анықталса, онда 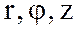 шамалары М нүктесінің цилиндрлік координаттары болады. М нүктесінің декарттық және цилиндрлік координаттарының арасындағы байланыс мына формулалармен анықталады (10-сурет):
шамалары М нүктесінің цилиндрлік координаттары болады. М нүктесінің декарттық және цилиндрлік координаттарының арасындағы байланыс мына формулалармен анықталады (10-сурет): 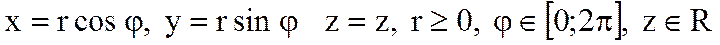 x,y,z координаттарын
x,y,z координаттарын 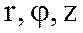 координаталарымен ауыстыру якобианы:
координаталарымен ауыстыру якобианы: 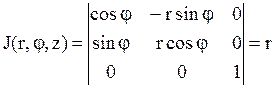 болады.Сондықтан 3 еселі интегралда айнымалы ауыстыру
болады.Сондықтан 3 еселі интегралда айнымалы ауыстыру 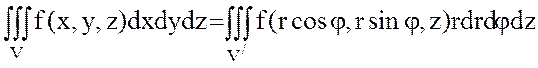
10-сурет.
3) Сфералық координаттар. Оxyz кеңістігінде М нүктесінің орнын:
а) О нүктесінен М нүктесіне дейінгі қашықтық 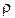 ;
;
б) ОМ кесіндісі мен Оz өсінің оң бағыты арасындағы бұрыш 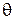 ;
;
в) ОМ кесіндінің Оху жазықтығындағы проекциясы ОМ1 мен Ох өсінің оң бағыты арасындағы бұрыш 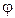 арқылы анықтасақ, онда осы
арқылы анықтасақ, онда осы 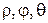 шамалары М нүктесінің сфералық координаттары болады. М нүктесінің декарттық және сфералық координаттар арасындағы байланыс мына формулар арқылы анықталады (суретке қара):
шамалары М нүктесінің сфералық координаттары болады. М нүктесінің декарттық және сфералық координаттар арасындағы байланыс мына формулар арқылы анықталады (суретке қара): 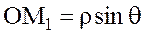
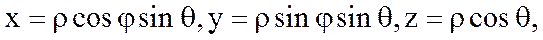
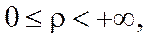
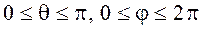
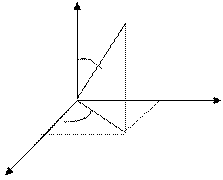 11-сурет
11-сурет
Декарттық координаттарды сфералық координаттарға ауыстыру якобианы былайша анықталады:
 .
.
14. Бірінші және екінші текті қисық сызықты интегралдар.
Бірінші текті қисық сызықты интеграл. Үзіліссіз 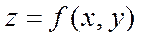 функциясының бөлікті – тегіс L қисығы бойынша бірінші ретті қисық сызықты интегралы деп мына шекті айтады:
функциясының бөлікті – тегіс L қисығы бойынша бірінші ретті қисық сызықты интегралы деп мына шекті айтады: 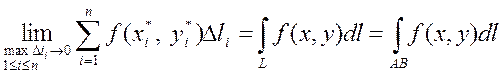 (1)мұндағы
(1)мұндағы 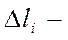 кез келген тәсілмен
кез келген тәсілмен 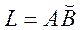 қисықты бөлгендегі
қисықты бөлгендегі 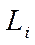 бөлікшенің (доғаның) ұзындығы,
бөлікшенің (доғаның) ұзындығы, 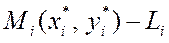 бөлікшенің кез – келген нүктесі, dl доғаның дифференциалы. Анықтамадан тікелей
бөлікшенің кез – келген нүктесі, dl доғаның дифференциалы. Анықтамадан тікелей
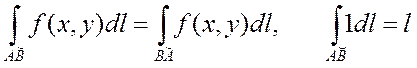 (2) теңдіктері шығады. Бірінші текті қисық сызықты интегралды есептеу анықталған интегралды есептеуге келтіріледі. Егер
(2) теңдіктері шығады. Бірінші текті қисық сызықты интегралды есептеу анықталған интегралды есептеуге келтіріледі. Егер 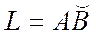 қисық
қисық 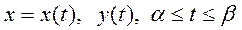 параметрлік түрде берілсе және
параметрлік түрде берілсе және 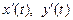 функциялар осы аралықта үзіліссіз болса, онда
функциялар осы аралықта үзіліссіз болса, онда
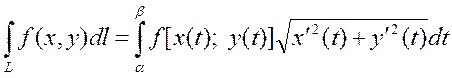 (3). Егер
(3). Егер 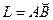 қисық
қисық 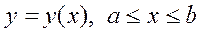 теңдеуімен берілсе және
теңдеуімен берілсе және 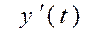 функциялар осы аралықта үзіліссіз болса, онда
функциялар осы аралықта үзіліссіз болса, онда  (4). Егер
(4). Егер  қисық
қисық 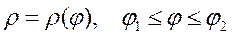 және
және  туынды
туынды 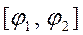 кесіндіде үзіліссіз болса, онда мына формула орынды:
кесіндіде үзіліссіз болса, онда мына формула орынды: 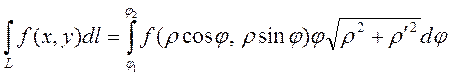 (5)
(5)
Кеңістіктегі тегіс қисық 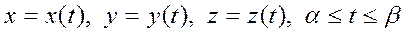 параметрлік теңдеулермен берілсе, әрі
параметрлік теңдеулермен берілсе, әрі 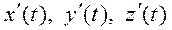 функциялары
функциялары 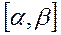 кесіндісінде үзіліссіз болса, онда мына формула орынды:
кесіндісінде үзіліссіз болса, онда мына формула орынды: 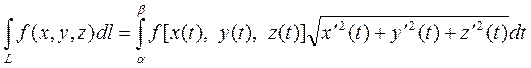 (6)
(6)
(1) теңдік жуықтап есептеулерде, ал (2) доғаның ұзындығын есептеуде қолданылады. Бірінші текті қисық сызықты интегралдар үшін анықталған интегралдың негізгі қасиеттері орындалады.
Екінші текті жалпы түрдегі қисық сызықты интеграл. есептеу. Бағытталған 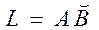 қисық бойынша екінші текті интегралдар
қисық бойынша екінші текті интегралдар 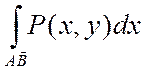 ,
, 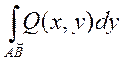 немесе жалпы
немесе жалпы 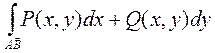 түрінде белгіленеді. Олар анықталған интегралдарға келтіру жолымен есептеледі. Мұнда
түрінде белгіленеді. Олар анықталған интегралдарға келтіру жолымен есептеледі. Мұнда 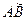 қисықтың бағыты өзгерсе, интегралдың мәні қарама-қарсы таңбға өзгереді, яғни
қисықтың бағыты өзгерсе, интегралдың мәні қарама-қарсы таңбға өзгереді, яғни

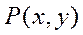 және
және 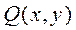 функциялары -
функциялары - 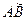 қисықта үзіліссіз функциялар.Егер
қисықта үзіліссіз функциялар.Егер 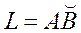 қисық
қисық 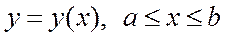 және
және 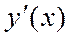 туынды
туынды 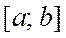 кесіндіде үзіліссіз болса, онда
кесіндіде үзіліссіз болса, онда 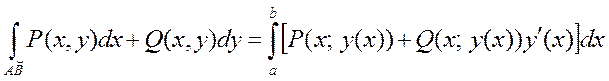
Егер 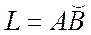 қисық
қисық 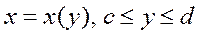 және
және 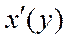 туынды
туынды 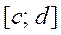 кесіндіде үзіліссіз болса, онда
кесіндіде үзіліссіз болса, онда
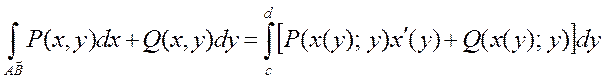
Егер 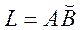 қисық
қисық 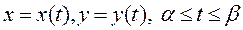 параметрлік теңдеулермен берілсе және
параметрлік теңдеулермен берілсе және 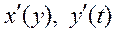 туындылар осы аралықта үзіліссіз болса, онда
туындылар осы аралықта үзіліссіз болса, онда
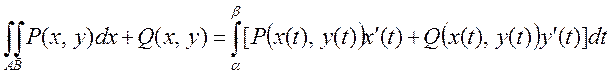
Кеңістіктегі 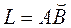 тегіс қисық
тегіс қисық 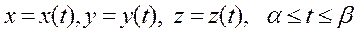 параметр лік теңдеулермен берілсе онда мына формула орындалады.
параметр лік теңдеулермен берілсе онда мына формула орындалады. 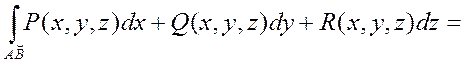
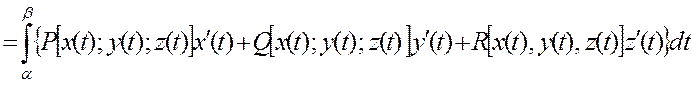 Мұндағы
Мұндағы 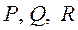 функциялары
функциялары 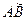 қисықта үзіліссіз функциялар. Екінші текті қисық сызықты интеграл үшін анықталған интегралдың негізгі қасиеттері орынды.
қисықта үзіліссіз функциялар. Екінші текті қисық сызықты интеграл үшін анықталған интегралдың негізгі қасиеттері орынды.
Date: 2015-05-22; view: 2226; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |