Квантово-механическое описание

С точки зрения квантовой механики, состояние любой системы должно описываться некоторым квантово-механическим вектором состояния | j ñ, и задача построения КМ-описания сводится к установлению явного вида этого вектора. Стандартный способ детализации вектора состояния сводится к его разложению по некоторому базисному набору таких векторов, о которых уже имеются все необходимые сведения. Базисные наборы, как известно, порождаются спектральными анализаторами — приборами для измерения наблюдаемых. Сконструируем прибор для измерения наблюдаемой х. Он выглядит весьма просто и представляет собой набор детекторов, расположенных друг за другом (без промежутков) вдоль оси х. Если сработает детектор, расположенный в точке х = х_i, то это означает, что измерение координаты дало результат х = х_i. Зная относительные частоты срабатывания детекторов, можно найти амплитуды вероятности срабатывания для каждого детектора (С_i) и соответствующие вероятности Р_i = | С_i | ².

Такой прибор порождает набор базисных состояний, в каждом из которых координата х имеет строго определенное значение:

если частица находится в базисном состоянии, обозначаемом кет-вектором | i ñ, то ее координата х имеет строго определенное значение х = х_i.

В результате мы имеем возможность представить произвольный вектор состояния | j ñ в виде ЛК:

| j ñ = C ₁| 1 ñ + C ₂| 2 ñ +... + C_n | n ñ

Эквивалентная схема такого прибора выглядит следующим образом:

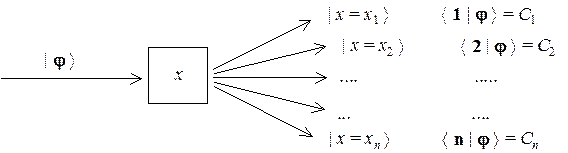
Оставаясь в рамках конкретной задачи, можно абстрагироваться от базисного набора и описать вектор его координатным представлением, состоящим только из чисел-координат:

| j ñ ~ (C₁, C ₂,..., C_n)

Подчеркнем, что каждое базисное состояние соответствует определенной точке на оси х. Поскольку таких точек бесконечно много, то и слагаемых в нашей ЛК, и чисел-координат будет бесконечно много. Поэтому в данной ситуации удобно описывать бесконечную совокупность чисел-координат в виде волновой функции j(х), зависящей, для данного случая, только от одной координаты х и некоторых внутренних параметров частицы (масса, спин и т.д.). Кроме того, волновая функция может зависеть от времени, причем эта зависимость описывается уравнением Шредингера:

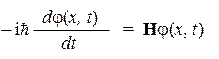
где Н — оператор Гамильтона (гамильтониан), i — мнимая единица, h — постоянная Планка.

Проблема установления зависимости волновой функции от времени часто встречается в КМ. В большинстве случаев эта задача может быть решена без знания явного вида гамильтониана. Среди всех возможных волновых функций выберем некоторые специальные, которые удовлетворяют уравнению на собственные значения для оператора Гамильтона:

H y _k = E_k y _k

Такие функции описывают КМ-состояния, называемые стационарными. Их отличительной особенностью является строго определенное и постоянное во времени значение энергии (Е = E_i = const).

Поскольку собственные функции (векторы) любого линейного оператора образуют один из базисов ЛП, то произвольная функция (вектор) может быть представлена в виде разложения по базису стационарных функций:

j(x, t) = D ₁y₁ + D ₁y₁ +... + D_r y _r

После того, как будет установлен вид зависимости собственных функций гамильтониана (y _k) от времени, становится известным и вид временной зависимости для произвольной функции с заданным набором коэффициентов (D_i).

Волновые функции стационарных состояний отличаются одной важной особенностью: если подставить любую из них в уравнение Шредингера, то из операторного, оно переходит в обыкновенное дифференциальное уравнение с разделяющимися переменными:

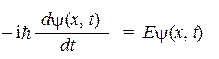
где Е — энергия стационарного состояния (собственное значение гамильтониана, соответствующее данному состоянию).

Такое уравнение может быть легко проинтегрировано. Его решения (т.е. волновые функции стационарных состояний) имеют стандартный вид:

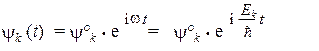
где Е_k — энергия данного стационарного состояния, а y° _k — константы интегрирования, не зависящие от времени. Ясно, что зависимость волновой функции от координаты х должна заключаться именно в этих константах, которые представляют собой некоторые функции только переменной х (но не времени):

y° _k = y _k (х)

Такие функции называются пространственными множителями (частями) волновых функций.

Установление полного вида волновой функции требует знания и вида пространственного множителя, и временной экспоненты. Если зависимость от времени для стационарных состояний всегда имеет стандартный вид, независимо от конкретного устройства системы (свободная частица, атом, молекула и т.д.), то вид пространственного множителя является специфичным для каждого конкретного случая. Проблема установления этого вида сводится к решению уравнения на собственные значения для оператора Гамильтона, причем знание явного вида гамильтониана является в этом случае обязательным.

Для случая свободной частицы, ввиду отсутствия внешних воздействий, оператор Гамильтона состоит только из оператора кинетической энергии:

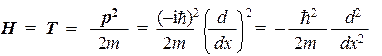
Тогда явный вид уравнения на собственные значения таков:

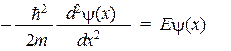
Это простое дифференциальное уравнение с разделяющимися переменными легко интегрируется. Оно имеет два частных решения:

y⁺(х) = A × е ^{i kx} и y^– (х) = B × e^{–i kx}

Общее решение является суммой частных:

y(х) = A × е ^{i (kx)} + B × e^{– i (kx)}

причем должно выполняться условие нормировки А ² + В ² = 1. Полный набор этих состояний можно изобразить посредством плоскости с координатными осями А и В:

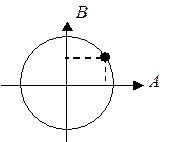
Из формулы

y(х) = A × е ^{i kx} + B × e^{–i kx} = A × y ⁺ + B × y ^–

видно, что все в принципе возможные состояния с определенным значением энергии являются линейной оболочкой двух особых состояний (y⁺ и y^–), составляющих двумерный базис. Любая точка изображенной окружности представляет возможный набор коэффициентов А и В, и соответствующее стационарное состояние. Конкретные значения коэффициентов А и В зависят от начальных условий.

Чтобы найти константу k, продифференцируем дважды любое частное решение и подставим вторую производную вместо левой части уравнения:

d ²[y(х)]/ dx ² = – k ² [y(х)] и – k ² [y(х)] = (–2 mE /h²) [y(х)].

Отсюда получим, что k = ±(2 mE)^0,5/h = ± p /h, где новая константа р называется квантовомеханическим импульсом. Следовательно, пространственные части волновых функций стационарных состояний должны иметь вид:

y(х) = А • ехр [ i (p /h) x ] + В • ехр [– i (p /h) x ]

Таким образом, для каждого определенного значения наблюдаемых Е и р получаем целую совокупность стационарных состояний, описываемых суперпозиционными волновыми функциями y(х). Характерная особенность полученных функций заключается в следующем: если мы будем измерять величину энергии, мы всегда получим один и тот же результат — число Е. При измерении импульса мы будем получать строго определенный результат — число | р | — только для модуля этого вектора, но знак, определяющий направление вектора импульса (и направление движения частицы) будет получаться различным, а именно: с вероятностью А ² будем находить число + р и с вероятностью В ² — число – р (заметим, что на возможные численные значения энергии и модуля импульса никаких ограничений не накладывается).

Другими словами, суперпозиционные функции описывают суперпозиционные состояния, в которых направление движения частицы не определено. Среди них, однако, можно выделить два специальных состояния, для которых как модуль, так и знак вектора импульса будет строго определен:

y⁺ = е ^{i kx} = е ^{i(+ р /h) x} (А = 1, В = 0)

y^– = e^{–i kx} = e ^{i(– р /h) x} (А = 0, В = 1)

Поскольку обе эти функции являются комплексными, то их конкретные значения (при заданном х) могут быть изображены вектором-стрелкой единичной длины в комплексной плоскости, которую удобно расположить перпендикулярно оси х (направлению движения частицы). При перемещении вдоль оси х эта стрелка будет поворачиваться в комплексной плоскости (вокруг оси х) с частотой, определяемой волновым вектором k = p /h. Ясно, что конец стрелки-амплитуды будет описывать спираль, закрученную по часовой стрелке или против нее, в зависимости от направления движения частицы (знака импульса).

Располагая выражениями для пространственной части волновой функции, можно проанализировать характер распределения частицы в пространстве. Для установления этого характера достаточно найти квадрат волновой функции, который показывает зависимость вероятности найти частицу в определенной точке от координаты этой точки:

Р(х) = y*(х) • y(х) = |y(х)| ²

Рассмотрим такие зависимости для базисных функций y⁺ и y^–.

|y⁺| ² = е ^{i kx} × e ^{–i kx} = 1 |y^–| ² = е ^{–i kx} × e^{i kx} = 1

Из полученных формул видно, что для этих двух состояний зависимость вероятности от координаты х отсутствует. Другими словами, все точки оси х полностью эквивалентны друг другу.

Необходимо отметить важную особенность полученного результата: в рассмотренных двух состояниях значения одной из наблюдаемых — импульса — строго определены, а значения другой наблюдаемой — пространственной координаты х — полностью неопределенны. Полезно построить графические изображения функций распределения для этих наблюдаемых:

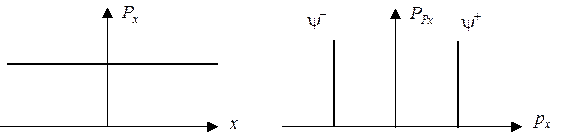
из которых ясно видно, что одна из функций (Р_х) бесконечно широкая, а другая (Р_Рх) — бесконечно узкая.

Такая связь между двумя наблюдаемыми является проявлением важного КМ-принципа — принципа неопределенности (Гейзенберг). Сами наблюдаемые, связанные в отношении их определенности, называются совместно неизмеримыми (несоизмеримыми, сопряженными).

Как во всяком ЛВП, в двумерном пространстве стационарных функций с определенным значением энергии можно выбрать не один базис, а бесконечно много таких базисов:

y(х) = A • y ⁺ + B • y ^– = С • y ' + D • y '' =.....

Рассмотрим еще один базис, состоящий из двух следующих функций:

y ' = А (е ^{i kx} + e ^{–i kx} ) (А = В)

y '' = А (е ^{i kx} – e ^{–i kx} ) (А = – В)

Ввиду равенства модулей коэффициентов (А ² = В ²), формулы для этих двух функций могут быть преобразованы с использованием тригонометрического представления комплексных экспонент: exp (±i • q) = cosq ± i • sinq. Тогда получим одну чисто действительную функцию и одну чисто мнимую функцию:

y ' = 2 А • cos (kx)

y ' = 2 iА • sin (kx)

Графики этих функций имеют вид не спиралей, как в предыдущем случае, а вид плоских кривых — косинусоиды, лежащей в плоскости, образованной осью х и осью действительных чисел, и синусоиды, лежащей в плоскости, образованной осью х и осью мнимых чисел:

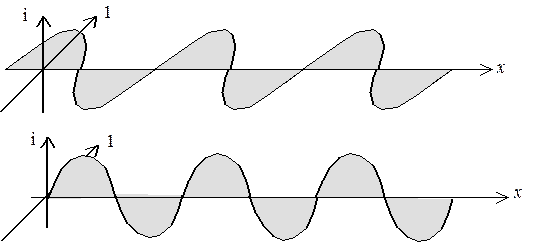
Для функций y ⁺ и y ^– модуль всюду сохранял свое значение, равное 1, а от координаты х зависела только фаза (q = kx). В данном случае ситуация противоположная: фазы функций y' и y'' сохраняются неизменными (0 и p/2, соответственно), тогда как модули изменяются с координатой х по гармоническому закону. Такой характер изменения приводит к тому, что в некоторых точках оси х значение волновой функции максимально, зато в других равно 0. Точки, в которых y = 0, называются узлами (узловыми точками).

Возведение этих двух функций в квадрат приведет к получению двух функций распределения вероятностей: P'(х) = | y' | ² и P''(х) = | y'' | ², которые также будут иметь вид гармонических волн, сдвинутых относительно друг друга на четверть периода:

Характерная особенность данных функций распределения — их пространственная неоднородность, доходящая до обращения вероятности в некоторых точках (в узлах) в 0. Вся ось х разбивается этими узлами на конечные ячейки длины D х = p/ k, внутри которых частица в определенной степени локализована — вероятность для центра ячейки много больше, чем для ее краев. Можно сказать, что степень пространственной локализации в состояниях y' и y'' является максимально возможной.

Другая особенность данных состояний обусловлена равенством А ² = В ², что приводит к заключению о невозможности определения направления вектора импульса частицы. При попытках измерения этой наблюдаемой будут получаться оба значения с равной вероятностью Р⁺ = А ² = 1/2 и Р^– = В ² = 1/2. Такой результат снова является следствием принципа неопределенности: увеличив пространственную локализацию частицы, мы уменьшили определенность сопряженной величины — проекции импульса на направление движения.

Вопросы для самоконтроля

1. В чем различие между физическими и математическими моделями? Для чего нужны физические модели?

2. Дайте определение понятия "свободная частица". Каковы особенности этой модели, отличающие ее от остальных?

3. Какими величинами характеризуются стационарные состояния свободной частицы?

4. Укажите основные отличия классического описания свободной частицы от квантово-механического.

5. Для описания каких типов реальных объектов может быть использована модель свободной частицы?

Список рекомендуемой литературы

Введение в квантовую химию (под ред. С. Накагура). М.: Мир, 1982.

Заградник Р., Полак Р. Основы квантовой химии. М.: Мир, 1979.

Мелешина А.М. Курс квантовой механики для химиков. М.: ВШ, 1980.

Минкин В.И., Симкин Б.Я., Миняев Р.М. Теория строения молекул. Ростов на Дону.: Феникс, 1997.

Симкин Б.Я., и др. Задачи по теории строения молекул. Ростов на Дону.: Феникс, 1997.

Суханов А.Д. Лекции по квантовой физике. М.: ВШ, 1991.

Шпольский Э.В. Атомная физика. Т. 1 и 2. М.: Наука, 1984.

Фейнман Р. и др. Фейнмановские лекции по физике. М.: Мир, 1967. Т. 8, 9.

Хабердитцл В. Строение материи и химическая связь. М.: Мир, 1974.

Хедвиг П. Прикладная квантовая химия. М.: Мир, 1977.

Эрдеи-Груз Т. Основы строения материи. М.: Мир, 1976.