
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоремы сложения и умножения вероятностей
1. Вероятность правильного оформления счета на предприятии составляет 0,95. Во время аудиторской проверки были взяты два счета. Какова вероятность того, что только один из них оформлен правильно?
2. Два охотника стреляют в волка, причем каждый делает по одному выстрелу. Для первого охотника вероятность попадания в цель равна 0,7, для второго – 0,6. Какова вероятность попадания в волка хотя бы при одном выстреле?
3. Из колоды в 36 карт наугад вынимают одну. Какова вероятность, что будут вынуты пики или туз?
4. Слово «ананас» составлено из букв разрезной азбуки. Карточки с буквами перемешивают, из них случайным образом берут по очереди 3 карточки и выкладывают в ряд. Какова вероятность, что из них образуется слово «сан»?
5. В лабиринте на правильном маршруте имеются 3 развилки, на каждой из которых нужно выбирать одно из двух направлений. Какова вероятность, что испытуемый пройдет лабиринт с первой попытки?
6. Два стрелка одновременно стреляют по мишени. Вероятности попадания для них равны соответственно 0,4 и 0,7. Какова вероятность ровно одного попадания?
7. Из карточек с буквами составлено слово «колокол». Карточки перемешиваются, из них случайным образом отбирают 4 и выкладываются в ряд. Какова вероятность, что они образуют слово «клок»?
8. Два студента ищут нужную им книгу в книжных магазинах. Вероятность того, что книга будет найдена первым студентом, равна 0,5, вторым – 0,7. Какова вероятность того, что только один из студентов найдет книгу?
9. В первой урне 3 белых и 5 черных шаров, во второй - 2 белых и 4 черных. Из первой урны во вторую случайным образом переложен один шар, затем извлечен шар из второй урны. Какова вероятность, что оба этих шара белые?
10. Два стрелка одновременно стреляют по мишени. Вероятности попадания для них равны соответственно 0,4 и 0,5. Какова вероятность хотя бы одного попадания?
11. Вероятность правильного оформления накладной при передаче продукции равна 0,8. Найти вероятность того, что из трех накладных все оформлены правильно, если события оформления накладных независимы.
12. В урне 3 белых и 5 черных шаров. По очереди вынимают 2 шара без возвращения. Какова вероятность, что первый шар черный, а второй белый?
13. В первой урне 3 белых и 5 черных шаров, во второй - 2 белых и 4 черных. Из первой урны во вторую случайным образом переложен один шар, затем извлечен шар из второй урны. Какова вероятность, что оба этих шара черные?
14. Слово "шарада" составлено из букв разрезной азбуки. Карточки с буквами перемешивают, из них случайным образом берут по очереди и выкладывают в ряд 3 карточки. Какова вероятность, что из них образуется слово "шар"?
15. Вероятность безотказной работы двух независимо работающих сигнализаторов соответственно равна 0,6 и 0,7. Найти вероятность того, что сработают: а) оба сигнализатора; б) хотя бы один сигнализатор.
16. В урне 3 белых и 5 черных шаров. По очереди вынимают 2 шара без возвращения. Какова вероятность, что первый шар белый, а второй черный?
17. Имеется два ящика, в каждом по 10 деталей; в первом ящике 8, во втором 7 стандартных деталей. Из каждого ящика наугад вынимают по одной детали. Какова вероятность, что они обе стандартные?
18. В группе из 24 студентов пятеро не подготовились к занятию. Наудачу вызваны два студента. Какова вероятность того, что оба они готовы к занятию?
19. Для некоторой местности число пасмурных дней в июле равно 6. Найти вероятность того, что 1 и 2 июля наудачу выбранного года будет ясная погода?
20. Экспедиция издательства отправила газеты в два почтовых отделения. Вероятность своевременной доставки в первое отделение равно 0,9, во второе – 0,8. Найти вероятности следующих событий: а) оба отделения получили газеты вовремя; б) только одно отделение получило газеты вовремя.
Формула полной вероятности и формула Байеса 
1. В магазин поступили партии обуви с двух фабрик: 30 % - с первой и 70 % - со второй. В продукции первой фабрики 30 % обуви коричневого цвета, в продукции второй - 80 %. Какова вероятность, что наугад взятая пара обуви окажется коричневого цвета?
2. В первой коробке 3 белых и 4 черных шара, во второй - 5 белых и 2 черных. Из первой коробки во вторую случайным образом переложили один шар, перемешали и извлекли шар из второй коробки. Какова вероятность, что он белый?
3. В группе спортсменов 20 лыжников и 8 бегунов. Вероятность выполнить квалификационную норму для лыжника равна 0,8, для бегуна - 0,7. Спортсмен выполнил норму. Какова вероятность того, что он лыжник?
4. В двух колодах по 36 карт. Из первой колоды наудачу вынимается карта и кладется во вторую колоду, из которой затем после перемешивания вынимается наудачу одна карта. Найти вероятность того, что эта карта бубновой масти.
5. В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).
6. В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.
7. В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?
8. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
9. Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед.
10. Два автомата производят одинаковые детали, которые поступают на конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.
11. В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.
12. В ящике содержится 12 деталей, изготовленных на заводе №1, 20 деталей – на заводе №2 и 18 деталей - на заводе №3. вероятность того, что деталь изготовлена на заводе %1, отличного качества, равна 0,9; для деталей, изготовленных на заводах №2 и№3, эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества.
13. Из 50 деталей 18 изготовлены в первом цехе, 20 - во втором, остальные - в третьем. Первый и третий цеха дают продукцию отличного качества с вероятностью 0,9, второй - с вероятностью 0,6. Взятая деталь оказалась отличного качества. Какова вероятность того, что деталь изготовлена во втором цехе?
14. В группе 30 студентов. Из них отличников – 5, хорошистов -7, троечников 14, остальные двоечники. Вероятность сдачи экзамена отличником равна 0,95, хорошистом – 0,8, троечником – 0,6, двоечником -0,3. какова вероятность тог, что произвольно вызванный студент сдаст экзамен.
15. В специализированную больницу поступают в среднем 50% больных заболеванием Х, 30% - с заболеванием Y, 20% - с заболеванием Z. Вероятность полного излечения болезни Х равна 0,7; для болезней Y и Z эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдает заболеванием Х.
16. Три стрелка произвели залп, причем одна пуля поразила мишень. Найти вероятность того, что третий стрелок попал в цель, если вероятности попадания в мишень первым, вторым, третьим стрелками соответственно равны 0,6, 0,5 и 0,4.
17. Один из трех независимо работающих элементов вычислительного устройства отказал. Найти вероятность того, что отказал первый элемент, если вероятности отказа первого, второго, третьего элементов соответственно равны 0,2, 0,4 и 0,3.
18. В двух колодах по 36 карт. Из первой колоды наудачу вынимается карта и кладется во вторую колоду, из которой затем после перемешивания вынимается наудачу одна карта. Найти вероятность того, что эта карта туз.
19. В обувную мастерскую для ремонта приносят сапоги и туфли в соотношении 2:3. Вероятность качественного ремонта для сапог равна 0,9, а для туфель – 0,85. проведена проверка качества одной пары обуви. Оказалось, что эта пара обуви отремонтирована качественно. Какова вероятность того, что это а) сапоги, б) туфли?
20. Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Найти вероятность того, что проверенное изделие стандартное.
Повторные независимые испытания 
1. Какова вероятность, что в серии из 5 выстрелов будет ровно одно попадание, если вероятность попадания при одном выстреле равна 0,3?
2. Всхожесть семян равна 0,8. Какова вероятность, что из 5 посеянных семян взойдет не менее двух?
3. Какова вероятность, что при 5 бросаниях игральной кости ни разу не выпадет 6 очков?
4. В институте девушки составляют 70 % от числа студентов. Какова вероятность, что среди первых четырех встретившихся студентов все девушки?
5. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются)?
6. Монету бросают пять раз. Найти вероятность того, что «герб» выпадет: а) менее двух раз; б) не менее двух раз.
7. Найти вероятность того, что событие А появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4.
8. В результате обследования были выделены семьи, имеющие по четыре ребенка. Считая вероятности появления мальчика и девочки в семье равными, определить вероятности появления в ней: а) одного мальчика; б) двух мальчиков.
9. Четыре покупателя приехали на оптовый склад. Вероятность того, что каждому из этих покупателей потребуется холодильник марки А, равна 0,4. Найти вероятность того, что холодильник потребуется: а) не менее чем двум покупателям; б) всем четырем покупателям; в) всем четырем покупателям.
10. Работают четыре магазина по продаже стиральных машин. Вероятность отказа покупателю в магазинах равна 0,1. Считая, что ассортимент товара в каждом магазине формируется независимо от других, определить вероятность того, что покупатель получит отказ в двух, в трех и в четырех магазинах.
11. В новом микрорайоне поставлено 10 000 кодовых замков на входных дверях домов. Вероятность выхода из строя одного замка в течение месяца равна а) 0,0002; б) 0,001. Найти вероятность того, что за месяц откажут два, три и пять замков.
12. Завод отправил в торговую сеть 500 изделий. Вероятность повреждения изделия в пути равна 0,002. найти вероятность того, что при транспортировке будет повреждено: а) ровно три изделия; б) более трех изделий.
13. На станциях отправления поездов находятся 1000 автоматов для продажи билетов. Вероятность выхода из строя одного автомата в течение часа равна 0,004. Какова вероятность того, что в течение часа из строя выйдут два, три и пять автоматов?
14. Обувной магазин продал 200 пар обуви. Вероятность того, что в магазин будет возвращена бракованная пара равна 0,01. Найти вероятность того, что из проданных пар обуви будет возвращено а) ровно 4 пары, б) ровно 5 пар.
15. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
16. Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
17. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков.
18. Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна 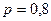 . Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.
. Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.
19. Вероятность появления события в каждом из 2100 независимых испытаний равна 0,7. Найти вероятность того, что событие появится: а) не менее 1470 и не более 1500 раз; б) не менее 1470 раз; в) не более 1469 раз.
20. Вероятность появления события в каждом из 21 независимых испытаний равна 0,7. Найти вероятность того, что событие появится в большинстве испытаний.
Date: 2015-05-08; view: 2067; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |