Домашнее задание №5. Математическая статистика

Задание 1

Медиана вариационного ряда 12, 13, 14, 16, 17, 17, 19 равна …
Варианты ответа

1. 7

2. 16

3. 15,5

4. 17

Решение:

Медианой вариационного ряда называется значение признака генеральной совокупности, приходящееся на середину вариационного ряда. В данном случае – это варианта, расположенная в середине вариационного ряда. В середине данного ряда располагается варианта 16.

Задание 2

Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 8, 10, 11, 13, 16. Тогда несмещенная оценка математического ожидания равна …
Варианты ответа

1. 12,0

2. 11,6

3. 11,4

4. 11,0

Решение:

Несмещенная оценка математического ожидания вычисляется по формуле: 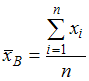. То есть .

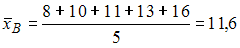Задание 3

Точечная оценка математического ожидания нормально распределенного количественного признака равна 15. Тогда его интервальная оценка может иметь вид …

Задание 4

Левосторонняя критическая область может определяться из соотношения …

Задание 5

В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 4,5; 5,5; 6,5. Тогда несмещенная оценка дисперсии равна …

Задание 6

Дан доверительный интервал 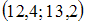для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …

Задание 7

Левосторонняя критическая область может определяться из соотношения …

Задание 8

Из генеральной совокупности извлечена выборка объема 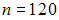, полигон частот которой имеет вид:

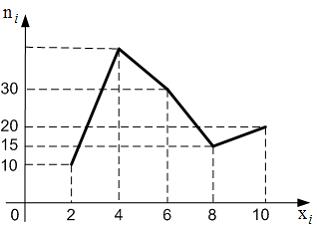
Тогда относительная частота варианты 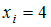в выборке равна …

Задание 9

Из генеральной совокупности извлечена выборка объема :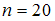

Тогда несмещенная оценка математического ожидания равна …

Задание 10

Дан доверительный интервал 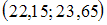для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …

Задание 11

Выборочное уравнение парной регрессии имеет вид . Тогда выборочный коэффициент корреляции может быть равен …

Задание 12

Из генеральной совокупности извлечена выборка объема :

Тогда значение 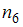равно …

Задание 13

В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 12,5; 14,5; 16,5. Тогда несмещенная оценка дисперсии равна …

Задание 14

Дан доверительный интервал 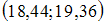для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …

Задание 15

При построении выборочного уравнения парной регрессии вычислены: выборочный коэффициент корреляции 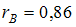и выборочные средние квадратические отклонения . Тогда выборочный коэффициент регрессии Y на X равен …

Задание 16

Из генеральной совокупности извлечена выборка объема :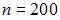

Тогда относительная частота варианты 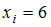равна …

Задание 17

В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 21,3; 24,3; 27,3. Тогда несмещенная оценка дисперсии равна …

Задание 18

Выборочное уравнение парной регрессии имеет вид 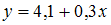, а выборочные средние квадратические отклонения равны: . Тогда выборочный коэффициент корреляции 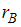равен …

Задание 19

Соотношением вида 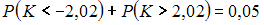можно определить …

Задание 20

Из генеральной совокупности извлечена выборка объема :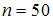

Тогда несмещенная оценка математического ожидания равна …

Задание 21

Выборочное уравнение парной регрессии имеет вид 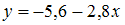. Тогда выборочный коэффициент регрессии равен …

Задание 22

Соотношением вида 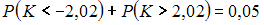можно определить …

Date: 2015-06-08; view: 2654; Нарушение авторских прав