
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Взаимодействие с веществом гамма-излучения
Гамма-излучение характеризуют интенсивностью, под которой понимают произведение энергии γ -квантов на их число, падающее ежесекундно на единицу поверхности, нормальной к потоку гамма-квантов.
Как и для любого вида электромагнитного излучения интенсивность γ-излучения точечного источника убывает обратно пропорционально квадрату расстояния от источника излучения (если не происходит его дополнительного поглощения в среде). Это определяется чисто геометрическими свойствами потока излучения, т.е. его расхождением по мере удаления от точечного источника излучения. Реально такое ослабление будет наблюдаться в абсолютном вакууме.
Гамма-излучение относится к сильнопроникающим излучениям. Но при прохождении через любое вещество будет происходить его поглощение этим веществом. Это поглощение может происходить благодаря взаимодействию γ-излучения с атомами, электронами и ядрами вещества, проявляющемуся в виде следующих эффектов [2, 3, 5]:
· фотоэффекта – состоящего в выбивании γ-квантом электронов из внутренних электронных оболочек атомов (чаще всего из К -оболочки), что приводит к его ионизации и появлению свободного электрона. Этот эффект преобладает при энергии γ-квантов ниже 0,5 МэВ;
· эффекта Комптона, который состоит в том, что γ-квант возбуждает электрон во внешней оболочке атома, передавая ему часть своей энергии, в результате чего уменьшается его энергия и изменяется направление (комптоновское рассеяние);
· образования пар – если γ-квант пролетает непосредственно вблизи ядра и при этом его энергия превышает 1,022 МэВ, то может образоваться электрон-позитронная пара;
· фотоядерных реакций, при которых гамма-кванты, поглощаясь ядром, возбуждают его, передавая ему свою энергию, и если эта энергия больше энергии связи нейтрона, протона или альфа-частицы, то эти частицы могут покидать ядро. На делящихся ядрах (235U, 239Pu и др.), если энергия гамма-кванта больше порога деления ядра, будет происходить его деление.
Вследствие всех этих взаимодействий при прохождении гамма-излучения через поглотитель его интенсивность уменьшается по закону [3]:
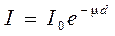 , (3.1)
, (3.1)
где I0 , I – интенсивность γ-излучения до и после прохождения через поглотитель;
μ – линейный коэффициент ослабления;
d – толщина поглотителя.
На рис. 3.1 представлена простая схема эксперимента по ослаблению. Когда гамма-излучение с интенсивностью I 0 падает на поглотитель толщиной d, интенсивность I излучения, прошедшего через поглотитель, описывается экспоненциальным выражением (3.1).
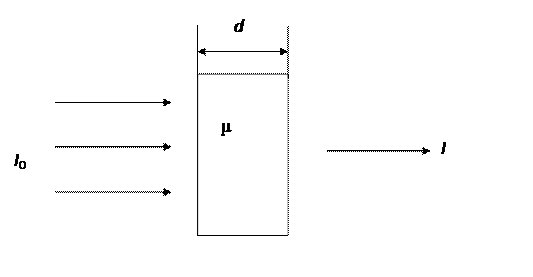
Рис. 3.1. Основной закон ослабления гамма-излучения
Интенсивность прошедшего излучения I является функцией энергии гамма-излучения, состава и толщины поглотителя. Отношение I/I 0 называется коэффициентом пропускания гамма-излучения. На рисунке 3.2 [16] показано экспоненциальное ослабление для трёх различных энергий гамма-излучений. Из рисунка видно, что коэффициент пропускания возрастает с увеличением энергии гамма-излучения и снижается с увеличением толщины поглотителя. Коэффициент μ в уравнении (3.1) называется линейным коэффициентом ослабления.

 Линейный коэффициент ослабления μ зависит от энергии γ-квантов и свойств поглощающего материала. Он имеет размерность м-1 и численно равен доле моноэнергетических гамма-квантов, выбывающих из параллельного пучка на единице пути излучения в веществе. Линейный коэффициент ослабления зависит от плотности и порядкового номера вещества, а также от энергии гамма-квантов. Например, свинец обладает высокой плотностью и большим атомным номером и пропускает гораздо меньшую долю падающего гамма-излучения, чем алюминий или сталь такой же толщины.
Линейный коэффициент ослабления μ зависит от энергии γ-квантов и свойств поглощающего материала. Он имеет размерность м-1 и численно равен доле моноэнергетических гамма-квантов, выбывающих из параллельного пучка на единице пути излучения в веществе. Линейный коэффициент ослабления зависит от плотности и порядкового номера вещества, а также от энергии гамма-квантов. Например, свинец обладает высокой плотностью и большим атомным номером и пропускает гораздо меньшую долю падающего гамма-излучения, чем алюминий или сталь такой же толщины.
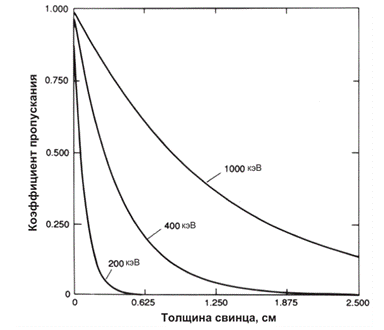
Рис. 3.2. Зависимость коэффициента пропускания гамма-квантов от толщины свинцового поглотителя
Значения линейного коэффициента ослабления гамма-излучения источника 60Со для различных материалов представлены в таблице 3.1, а их зависимость от энергии γ-квантов – в таблице 3.2 [1].
Толщину слоя поглотителя, необходимую для уменьшения интенсивности излучения в два раза называют полутолщиной d1/2 .
Из закона поглощения (3.1) следует, что полутолщина равна
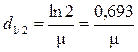 . (3.2)
. (3.2)
Таблица 3.1
Линейный коэффициент ослабления μ материалов γ-излучения Со-60
| Материал | Свинец | Сталь | Чугун | Бетон | Кирпич |
| ρ, кг/дм3 | 11,34 | 7,7 | 7,4 | 3,2-2,1 | 1,7-1,5 |
| μ, см-1 | 0,53 | 0,34 | 0,3 | 0,14-0,09 | 0,075-0,065 |
Таблица 3.2
Зависимость линейного коэффициента ослабления μ материалов
от энергии γ-квантов
| Е, МэВ | μ, см-1 | |||||
| Свинец | Вода | Алюминий | Железо | Графит | Воздух | |
| 0,10 | 0,171 | 0,455 | 2,91 | 0,342 | 2,00·10-4 | |
| 0,15 | 22,8 | 0,151 | 0,371 | 1,55 | 0,304 | 1,76·10-4 |
| 0,20 | 11,1 | 0,137 | 0,328 | 1,15 | 0,277 | 1,59·10-4 |
| 0,30 | 4,43 | 0,119 | 0,280 | 0,865 | 0,241 | 1,38·10-4 |
| 0,40 | 2,62 | 0,106 | 0,249 | 0,740 | 0,214 | 1,23·10-4 |
| 0,50 | 1,80 | 0,0966 | 0,227 | 0,661 | 0,196 | 1,12·10-4 |
| 0,80 | 0,999 | 0,0786 | 0,184 | 0,526 | 0,159 | 9,13·10-5 |
| 1,0 | 0,798 | 0,0279 | 0,165 | 0,471 | 0,143 | 8,21·10-5 |
| 1,5 | 0,591 | 0,0575 | 0,135 | 0,382 | 0,117 | 6,68·10-5 |
| 2,0 | 0,518 | 0,0493 | 0,116 | 0,334 | 0,0999 | 5,74·10-5 |
| 3,0 | 0,475 | 0,0396 | 0,0950 | 0,284 | 0,0801 | 4,63·10-5 |
| 4,0 | 0,472 | 0,0340 | 0,0834 | 0,260 | 0,0684 | 3,98·10-5 |
| 5,0 | 0,480 | 0,0302 | 0,0761 | 0,247 | 0,0603 | 3,54·10-5 |
| 8,0 | 0,519 | 0,0242 | 0,0651 | 0,233 | 0,0482 | 2,87·10-5 |
| 0,552 | 0,0220 | 0,0619 | 0,233 | 0,0439 | 2,62·10-5 | |
| 0,628 | 0,0193 | 0,0584 | 0,241 | 0,0380 | 2,31·10-5 | |
| 0,694 | 0,0180 | 0,0578 | 0,250 | 0,0351 | 2,19·10-5 | |
| 0,792 | 0,0170 | 0,0584 | 0,269 | 0,0329 | 2,08·10-5 | |
| 0,863 | 0,0166 | 0,0603 | 0,285 | 0,0320 | 2,06·10-5 | |
| 0,915 | 0,0166 | 0,0616 | 0,299 | 0,0320 | 2,08·10-5 |
Линейный коэффициент ослабления представляет собой простейший коэффициент ослабления, который можно измерить экспериментально, но он обычно не приводится в справочных таблицах ввиду зависимости от плотности поглощающего материала. Например, вода, лед и пар имеют различные линейные коэффициенты ослабления для одной и той же энергии, хотя они состоят из одного и того же вещества.
Гамма-кванты взаимодействуют, в основном, с атомными электронами, следовательно, коэффициент ослабления должен быть пропорционален плотности электронов P, которая пропорциональна объёмной плотности поглощающего материала. Для любого конкретного вещества отношение плотности электронов к объёмной плотности этого вещества является константой Z/A, независимой от объёмной плотности. Отношение Z/A является почти постояным для всех элементов, кроме самых тяжелых элементов и водорода [16]:
P=Z ρ / A, (3.3)
где P — плотность электронов;
Z — атомный номер;
ρ — массовая плотность;
A — массовое число.
Если поделить линейный коэффициент ослабления на плотность вещества ρ, то получится массовый коэффициент ослабления, не зависящий от плотности вещества [2]:
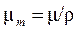 . (3.4)
. (3.4)
Массовый коэффициент ослабления измеряется в см2/г (в системе СИ – м2/кг) и зависит только от порядкового номера вещества и энергии гамма-квантов. Судя по единице измерения этого коэффициента, можно рассматривать его как эффективное сечение взаимодействия электронов на единицу массы поглотителя. Массовый коэффициент ослабления может быть записан через сечение реакции σ (см2):
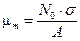 , (3.5)
, (3.5)
где N 0 — число Авогадро (6,02 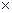 1023);
1023);
А — массовое число поглощающего элемента.
Сечение взаимодействия σ i по своему определению аналогичны сечениям реакции, т.е. определяет вероятность протекания i -го процесса при взаимодействии гамма-кванта с атомом. Оно связано с линейными коэффициентами ослабления μ i формулой
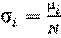 , (3.6)
, (3.6)
где N – количество атомов вещества в 1 см3;
i – краткое обозначение фотоэффекта (ф), комптон-эффекта (к) и эффекта образования пар электрон-позитрон (п).
Сечения выражаются в барнах на атом.
Используя массовый коэффициент ослабления, уравнение (3.1) можно представить следующим образом [16]:
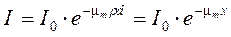 , (3.7) где x = ρ d.
, (3.7) где x = ρ d.
Массовый коэффициент ослабления не зависит от плотности, а зависит от энергии фотонов и атомного номера поглотителя. На рисунках 3.3 и 3.4 показана зависимость 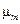 от энергии фотонов в диапазоне от 0.01 до 100 МэВ для групп элементов от углерода до свинца [14]. Этот коэффициент чаще приводится в таблицах, чем линейный коэффициент ослабления, поскольку он количественно определяет вероятность взаимодействия гамма-квантов с конкретным элементом.
от энергии фотонов в диапазоне от 0.01 до 100 МэВ для групп элементов от углерода до свинца [14]. Этот коэффициент чаще приводится в таблицах, чем линейный коэффициент ослабления, поскольку он количественно определяет вероятность взаимодействия гамма-квантов с конкретным элементом.
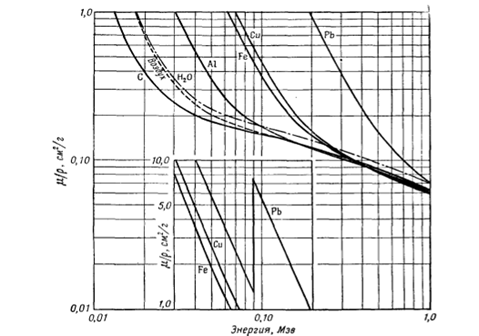
Рис. 3.3. Зависимость полного массового коэффициента поглощения от энергии фотонов для различных материалов (диапазон энергии от 0,01 до 1 МэВ)
|

В справочнике [3] приведены таблицы зависимостей линейного и массового коэффициентов ослабления и длины свободного пробега гамма-квантов от их энергии в диапазоне от 0,01 до 10 МэВ для различных веществ.
Взаимодействие гамма-излучения со сложным веществом характеризуется эффективным порядковым номером Z эфф этого вещества. Он равен порядковому номеру такого условного простого вещества, массовый коэффициент ослабления которого при любой энергии гамма-квантов совпадает с массовым коэффициентом ослабления данного сложного вещества. Его рассчитывают из соотношения [2]:
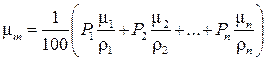 , (3.8)
, (3.8)
где Р1, Р2, …, Рn – весовое процентное содержание составляющих веществ в сложном веществе;
μ1/ρ1 , μ2/ρ2 , …, μ n /ρ n – массовые коэффициенты ослабления составляющих веществ в сложном веществе.
С учётом названных выше трёх основных эффектов взаимодействия гамма-излучения с веществом полный линейный коэффициент ослабления будет состоять из трёх составляющих, определяемых фотоэффектом, комптон-эффектом и эффектом порождения пар:
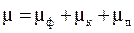 . (3.9)
. (3.9)
Каждый из них различным образом зависит от порядкового номера вещества и энергии гамма-квантов.
При фотоэффекте гамма-квант поглощается атомом, а из атома вырывается электрон (рисунок 3.5).
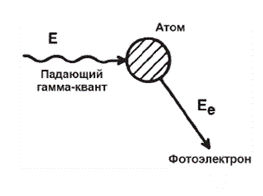
Рис. 3.5. Схема процесса фотоэлектрического поглощения
Часть энергии гамма-кванта, равная энергии связи εе , расходуется на отрыв электрона от атома, а остальная часть преобразуется в кинетическую энергию этого электрона Ее:
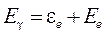 . (3.10)
. (3.10)
Первая особенность фотоэффекта заключается в том, что он протекает только тогда, когда энергия гамма-кванта больше энергии связи электрона в соответствующей оболочке атома. Если энергия гамма-кванта меньше энергии связи электрона в К -оболочке, но больше, чем в L -оболочке, то фотоэффект может идти на всех оболочках атома, кроме К -оболочки, и т.д.
Вторая особенность состоит в увеличении фотоэлектрического поглощения гамма-квантов с ростом энергии связи электронов в атоме. На слабо связанных электронах фотоэффект практически не наблюдается, а свободные электроны вообще не поглощают гамма-кванты. Линейный коэффициент ослабления фотоэффекта пропорционален отношению Z4/E γ 3.
Эта пропорциональность является лишь приблизительной, поскольку показатель степени Z изменяется в диапазоне от 4,0 до 4,8. С уменьшением энергии гамма-кванта вероятность фотоэлектрического поглощения быстро растет (см. рис. 3.6) [16]. Фотоэлектрическое поглощение является преобладающим процессом взаимодействия для гамма-квантов низких энергий, рентгеновских квантов и тормозного излучения.
Фотоэффект в основном наблюдается на K - и L -оболочках тяжёлых атомов при энергиях гамма-квантов до 10 МэВ. Коэффициент μф резко уменьшается с увеличением энергии гамма-квантов и при энергии около 10 МэВ приближается к нулю, т.е. фотоэлектроны не возникают. На рис. 3.6 представлен фотоэлектрический массовый коэффициент ослабления для свинца. Вероятность взаимодействия быстро возрастает с уменьшением энергии, но затем резко снижается при энергии гамма-кванта чуть ниже энергии связи K-электрона. Этот скачок называется K -краем. Ниже этой энергии гамма-квант не имеет достаточно энергии, чтобы выбить K -электрон. Ниже K -края вероятность взаимодействия снова возрастает до тех пор, пока энергия становится ниже энергий связи L -электронов. Такие скачки называются L I-, L II- , L III- - краями.
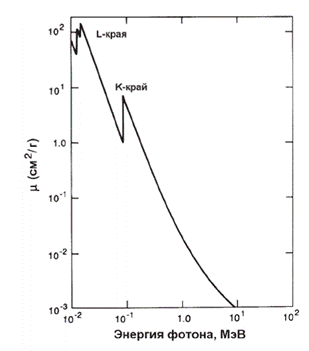
Рис. 3.6. Фотоэлектрический массовый коэффициент ослабления для свинца
На слабо связанных электронах атомов происходит рассеяние γ-квантов, называемое комптон-эффектом. При таком взаимодействии происходят как бы упругие столкновения γ-квантов с эквивалентной массой m γ = E/c2 с электронами массой me. Схематически такое столкновение представлено на рисунке 3.7. В каждом таком столкновении γ-квант передаёт часть своей энергии электрону, придавая ему кинетическую энергию. Поэтому такие электроны называют электронами отдачи. Кинетическая энергия электрона отдачи будет равна
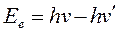 , (3.11)
, (3.11)
где v и 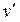 – частота γ-кванта до и после столкновения;
– частота γ-кванта до и после столкновения;
h – постоянная Планка.
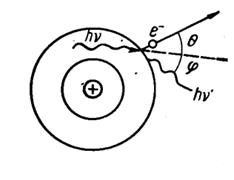
Рис. 3.7. Схема взаимодействия гамма-кванта с веществом
при Комптон-эффекте
После столкновения электрон отдачи и γ-квант разлетаются под углами θ и φ относительно первоначального направления движения γ-кванта. Учитывая законы сохранения энергии и импульса (количества движения), произойдёт изменение длины волны γ-кванта:
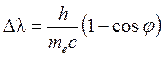 . (3.12)
. (3.12)
При касательных столкновениях γ-квант отклоняется на малые углы (φ ~ 0) и его длина волны изменяется незначительно. Максимальным оно будет при лобовых столкновениях (φ ~ 1800), достигая величины
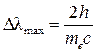 . (3.13)
. (3.13)
Энергия рассеянного гамма-кванта 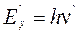 и электрона отдачи Ee связаны с начальной энергией гамма-кванта, с углами φ и θ соотношениями [2]:
и электрона отдачи Ee связаны с начальной энергией гамма-кванта, с углами φ и θ соотношениями [2]:
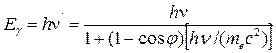 , (3.14)
, (3.14)
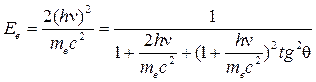 . (3.15)
. (3.15)
Так как взаимодействие γ-кванта с любым электроном независимо, то величина μ к пропорциональна плотности электронов Ne, которая, в свою очередь, пропорциональна порядковому номеру Z вещества. Зависимость μк от энергии γ-кванта h v и Z, полученная физиками Клейном, Нишиной и Таммом, имеет вид [3]:
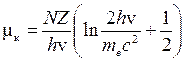 , (3.16)
, (3.16)
где N – число атомов в 1 см3 вещества.
Комптон-эффект идёт главным образом на слабосвязанных электронах внешних оболочек атомов. С увеличением энергии доля рассеянных γ-квантов уменьшается. Но убывание линейного коэффициента рассеяния μк происходит медленнее, чем μф. Поэтому в области энергий E γ > 0,5 МэВ комптон-эффект преобладает над фотоэффектом.
В спектрометрии гамма-излучения используется величина d μ к/dEe, называемая дифференциальным коэффициентом комптоновского рассеяния γ -квантов. Его физический смысл состоит в том, что он определяет количество электронов отдачи в единице объёма вещества, образуемое потоком гамма-квантов Ф с энергией Е γ, энергия которых заключена в интервале от нуля до максимального значения Ее макс. Теория Клейна-Нишины-Тамма позволяет получить аналитическое выражение для величины d μ к / dEe = Nd 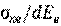 , где N – число атомов в единице объёма вещества. Для иллюстрации этой зависимости приведём графические распределения электронов отдачи для трёх фиксированных энергий гамма-квантов (рис. 3.8) [3]. В случае высоких энергий γ-квантов (более 2 МэВ) распределение электронов отдачи по энергии практически постоянно. Отклонение от постоянного значения (увеличение плотности распределения электронов отдачи) начинается при приближении их энергии к энергии γ-кванта, образуя так называемый комптоновский пик. При этом энергия электронов отдачи в комптоновском пике несколько ниже энергии породивших их гамма-квантов (что и видно из рисунка).
, где N – число атомов в единице объёма вещества. Для иллюстрации этой зависимости приведём графические распределения электронов отдачи для трёх фиксированных энергий гамма-квантов (рис. 3.8) [3]. В случае высоких энергий γ-квантов (более 2 МэВ) распределение электронов отдачи по энергии практически постоянно. Отклонение от постоянного значения (увеличение плотности распределения электронов отдачи) начинается при приближении их энергии к энергии γ-кванта, образуя так называемый комптоновский пик. При этом энергия электронов отдачи в комптоновском пике несколько ниже энергии породивших их гамма-квантов (что и видно из рисунка).
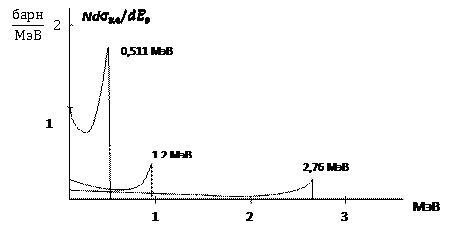 |
Рис. 3.8. Энергетическое распределение электронов отдачи
для γ-квантов различных энергий
Поскольку выше начальной энергии γ-квантов энергия электронов отдачи быть не может, после комптоновского пика распределение резко обрывается к нулю. При уменьшении энергии γ-квантов (менее 1,5 МэВ) равномерность распределения ниже комптоновского пика также нарушается. На рисунке 3.9 представлена зависимость энергии комптоновского края от энергии гамма-квантов. Из него следует, что с ростом энергии гамма-квантов различие в энергиях фотопика и комптоновского края сначала быстро растёт, но, начиная с энергий 100-200 кэВ это различие стремится к постоянной величине.
Эффект образования пар происходит при прохождении γ-кванта вблизи ядра, если его энергия превышает пороговое значение 1,022 МэВ. Вне поля ядра γ-квант не может образовать пару электрон-позитрон, т.к. в этом случае будет нарушен закон сохранения импульса. Хотя энергии в 1,022 МэВ достаточно, чтобы породить пару, но тогда импульс порождённых частиц должен быть равен нулю, тогда как γ-квант имеет импульс отличный от нуля и равный E γ /c. Однако, в поле ядра этот эффект становится возможным, поскольку в этом случае энергия и импульс γ-кванта распределяются между электроном, позитроном и ядром без нарушения законов сохранения. При этом, поскольку масса ядра в тысячи раз превышает массу электрона и позитрона, то оно получает ничтожную часть энергии γ-кванта, которая практически полностью распределяется между электроном и позитроном. Схематично эффект рождения пары электрон-позитрон представлен на рисунке 3.10.
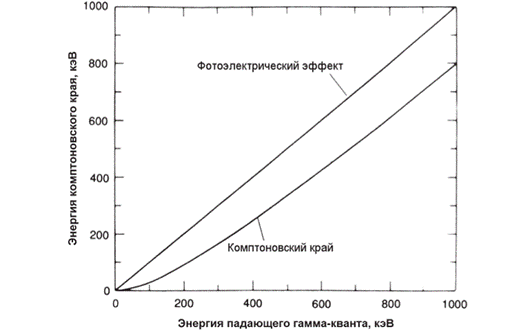
Рис. 3.9. Зависимость энергии комптоновского края от энергии гамма-кванта
|
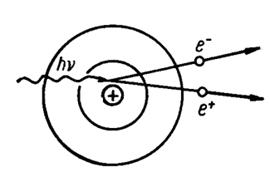
Рис. 3.10. Схема взаимодействия гамма-кванта с веществом
при эффекте образования пар
При превышении пороговой энергии 1,022 МэВ линейный коэффициент ослабления за счёт эффекта образования пар μп становится отличным от нуля и резко растёт, а при энергиях более 5 МэВ его действие становится определяющим. Это наглядно видно из рисунка 3.11 [3] на котором представлены зависимости линейного коэффициента ослабления гамма-излучения и его составляющих для свинца от энергии γ-квантов.
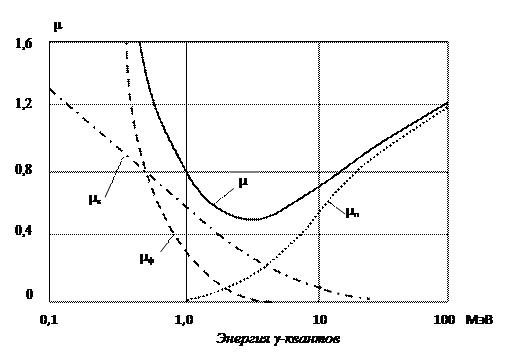 |
Рис. 3.11. Зависимость линейных коэффициентов ослабления гамма-излучения от энергии γ-квантов для свинца
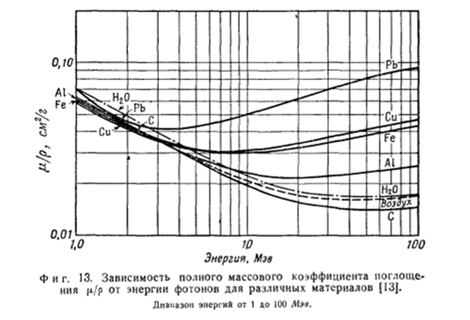
Все три процесса взаимодействия, описанные выше, вносят вклад в полный массовый коэффициент ослабления. Относительный вклад трёх процессов взаимодействия зависит от энергии гамма-кванта и атомного номера поглотителя. На рис. 3.12 [16] показан набор кривых массового ослабления, охватывающий широкий диапазон энергий и атомных номеров. Коэффициент ослабления для всех элементов, за исключением водорода, имеет резкий подъём в области низких энергий, который указывает, что в этой области преобладающим процессом взаимодействия является фотоэлектрическое поглощение. Расположение этого подъёма сильно зависит от атомного номера. Выше подъёма в области низких энергий значение массового коэффициента ослабления постепенно снижается, определяя область, в которой преобладающим взаимодействием является комптоновское рассеяние.
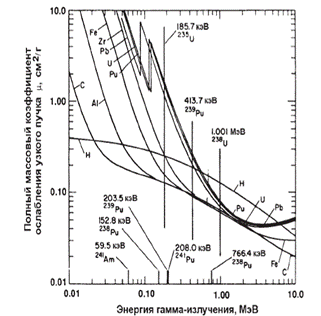
Рис. 3.12. Массовые коэффициенты ослабления некоторых элементов
(показаны энергии гамма-квантов, используемые обычно при
идентификации изотопов урана и плутония по гамма-излучению)
Массовые коэффициенты ослабления для всех элементов с атомным номером меньше, чем 25 (железо), практически идентичны в энергетическом диапазоне от 200 до 2000 кэВ. В диапазоне от 1 до 2 МэВ кривые ослабления сходятся для всех элементов. Форма кривой массового ослабления водорода показывает, что взаимодействие гамма-квантов с энергией больше 10 кэВ проходит почти исключительно путём комптоновского рассеяния. При энергиях выше 2 МэВ для элементов с высоким атомным номером Z важным становится процесс взаимодействия с образованием пар, и массовый коэффициент ослабления снова начинает расти [16].
Date: 2015-06-08; view: 8719; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |