Определение взаимосвязи между избыточностью и корректирующей способностью кодов

Важнейшей задачей теории кодирования является определение взаимосвязи между кратностью или длиной корректирующих ошибок и требуемой для этого цели избыточности кода, т.е. требуется определить какая минимально необходимая избыточность должна быть у разрабатываемого кода, чтобы данный код гарантировано исправлял ошибки требуемой (заданной) кратности или длины.

Кратность ошибки, как и вводимая в избыточность в код, чаще всего измеряется количеством двоичных символов или бит.

По величине вводимой избыточности принято оценивать эффективность разработанного или выбранного кода; если сравниваются два, три и т.д. кода, корректирующих ошибки одинаковой кратности, то наиболее эффективным считается код, который использует для этого меньшую избыточность. Данный код чаще всего и надо выбирать для практической реализации.

Коды, которые обеспечивают коррекцию ошибок равной кратности с другими кодами, но используют для этого меньшую избыточность (меньше проверочных символов), называются совершенными или плотно упакованными кодами.

Следовательно, совершенный код будет обеспечивать эффективное использование пропускной способности как канала связи, так и сети связи в целом.

Однако на практике совершенные коды часто технически просто нереализуемы; либо имеют высокую сложность реализации (требуется RG очень большой длины), либо обеспечивают коррекцию ошибок небольшой кратности: одиночные и двоичные ошибки [1-3,5-9].

Следовательно, при разработке или выборе кода важно правильно выбрать избыточность кода, т.е. какое минимально необходимое число проверочных символов «l» необходимо ввести в передаваемый информационный блок. Нетрудно видеть, что это число, т.е. «l» – число проверочных символов, будет зависеть от статистики ошибок в дискретном канале связи (ДКС).

Данная задача или проблема решается довольно просто, если требуется построить код, обнаруживающий либо одиночные (нечетные ошибки), либо двойные (четные) ошибки.

В первом случае для этого достаточно ввести один проверочный (контрольный) символ, а во втором случае – ввести два проверочных символа.

Абсолютная «l» и относительная «r» избыточность данных кодов будет составлять:

l₁=n₁k₁=1;

; (1.3)

l₂=n₂-k₂=2;

. (1.4)

Откуда следует, что относительная избыточность «r», которую можно назвать коэффициентом избыточности, стремится к 0, если n стремится к бесконечности, т. е. если k стремится к бесконечности.

Задача определения оптимального количества проверочных символов в кодовой последовательности существенно усложняется, когда требуется разработать или выбрать код, корректирующий ошибки. Общая идея исправления (коррекции) ошибок кратности не более t_исп двоичных символов состоит в следующем [1-3,8,9].

Общее число кодовых последовательностей n-разрядного кода, равное К_общ=2ⁿ, разбивается на N подклассов по числу N=K_pаз=2^k разрешенных кодовых последовательностей. Разбиение осуществляется таким образом, чтобы в каждый подкласс входили одна разрешенная и ближайшие к ней запрещенные кодовые последовательности. При декодировании определяется, какому подклассу принадлежит принятая кодовая последовательность. Если кодовая последовательность принята с ошибкой, т.е. является запрещенной, то она исправляется на разрешенную, принадлежащую тому же классу, что и запрещенная, т.е. из одного и того же подкласса.

Пусть имеется блоковый код с параметрами (n,k,d_o), который исправляет ошибки кратностью или длиной от «l» до «t» включительно.

Так как количество ошибок кратности «m» двоичных символов (m – общее обозначение ошибок) на длине «n» двоичных символов, равно числу сочетаний из «n» по «m», то общее количество ошибок (которое обозначим N) кратности от «l» до «t», возможных в одной кодовой последовательности, равно:

Двоичный блоковый код с параметрами (n,k,d_o) образует:

К_общ = 2ⁿ – общее число кодовых последовательностей;

К_раз = 2^k – количество разрешенных кодовых последовательностей;

К_корр = К_общ – К_раз = 2ⁿ – 2^k = 2^k – количество кодовых последовательностей, которые может код исправить.

Следовательно, значения К_общ и К_раз должны выбираться так, чтобы выполнялось неравенство:

К_раз* N ≤ К_общ – Краз или К_общ ≥ К_раз*(1+N_t).

Произведение К_общ* N характеризует общее число ошибок, которое может исправить (n,k,d_o)-код в К_раз разрешенных кодовых последовательностях.

Логарифмируя выражение 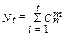можно получить выражение, которое позволяет определить необходимое число проверочных или избыточных двоичных символов для коррекции ошибок заданной кратности, а именно:

l = n – k ≥ log . (1.5)

Наиболее строго соотношение между параметрами линейных блоковых кодов n, k и l устанавливаются соответствующими границами:

- нижней границей Хэмминга;

- верхней границей Варшамова-Гильберта.

Эти границы устанавливаются следующими неравенствами [1-4]:

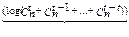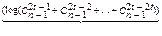< l < (1.6)

нижняя граница Хэмминга верхняя граница Варшамова-Гильберта

Для приближенных расчетов можно пользоваться формулой [1-3]:

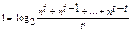(1.7)

Для кодов, используемых для обнаружения ошибок, и при заданном числе информационных символов (т.е. «k» = const), справедливо следующее выражение для определения «l» [1-5]:

l ≥ 1+log₂([(k+1)+ log₂(k+1)]. (1.8)

Для кодов корректирующих одиночные ошибки количество «l» проверочных символов может быть определено из решения следующих равенств-неравенств (формулы Хэмминга):

2ⁿ ≥ 2^k*(n + 1); (1.9) (1.9)

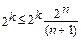;(1.10) (1.10)

n 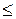2^l – 1. (1.11)

Для пользования последними тремя формулами необходимо иметь значение одного параметра, а два остальных находятся методом подбора.

Для кодов Хэмминга, с d_o=3, т.е. корректирующих одиночные ошибки, количество разрешенных кодовых последовательностей должно удовлетворять следующему неравенству:

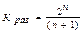,(1.12)

первые «k» символов кодовой последовательности кода используются в качестве информационных символов, и их число должно удовлетворять следующему неравенству:

(1.13)

При коррекции ошибок кратностью t > 3 двоичных символов выражения (1.9) – (1.13) существенно усложняются.

2 ЦИКЛИЧЕСКИЕ КОДЫ: ОПРЕДЕЛЕНИЕ,