
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод конечных элементов
Лекции 10-12
Метод конечных элементов
Метод конечных элементов
И вот, наконец, мы подошли к главной цели этого параграфа: обсуждению метода конечных элементов (МКЭ). Сразу следует сказать, что МКЭ представляет собой вариант метода Бубнова-Галеркина. Особенность МКЭ заключается в своеобразном выборе системы аппроксимирующих функций.
В предыдущем пункте было показано, что метод Бубнова-Галеркина дает наилучшие результаты. Однако метод этот достаточно трудоемок, поскольку требует вычисления интегралов. В рассмотренном примере это интегралы вида: 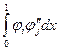 и
и 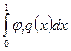 .
.
При решении не одномерных, а двух- и трехмерных задач трудоемкость вычисления таких интегралов многократно возрастает. Дело в том, что интегралы эти придется вычислять по всей области решения. А эта область может представлять собой фигуру очень сложной формы. Кроме того, большие сложности будут с выбором аппроксимирующих функций, которые, как отмечалось в самом начале этого раздела, должны удовлетворять заданным граничным условиям. Граница же двумерной области может быть кривой достаточно сложной формы.
Так вот, именно принятый в МКЭ выбор аппроксимирующих функций позволяет очень просто преодолеть обе эти сложности: 1) вычисление интегралов по области решения произвольной формы; 2) удовлетворение решения граничным условиям.
Сначала рассмотрим детально конечно-элементный подход на нашем примере одномерной задачи (1)
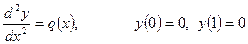
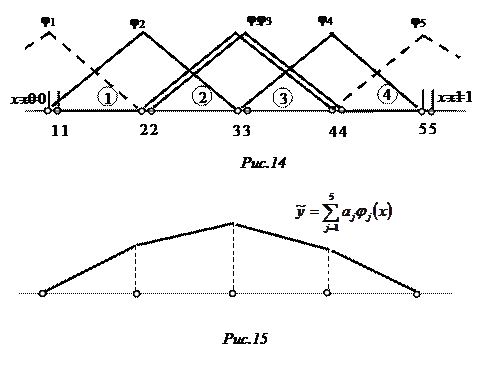
Область решения (отрезок [0,1]) разбивается на отрезки (см рис.14). Эти отрезки и называются конечными элементами (на рисунке они пронумерованы цифрами в кружках). Сразу отметим, что размеры этих конечных элементов могут быть произвольными. В отличие от метода конечных разностей, в методе конечных элементов неравномерность сетки разбиения не приводит к усложнению вычислений. Точки на границах конечных элементов называются узловыми точками или узлами.
Теперь, пожалуй, самое главное – выбор системы аппроксимирующих функций, которые должны представить приближенное решение в виде:
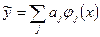 (33)
(33)
Функции эти выбираются следующим образом. Значение функции 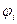 равно 1 в
равно 1 в  -том узле и равно 0 во всех остальных узлах. На рис.14 показана одна такая функция
-том узле и равно 0 во всех остальных узлах. На рис.14 показана одна такая функция  . Эта функция изменяется линейно в пределах конечных элементов, примыкающих к 3-му узлу и тождественно равна нулю на всех остальных конечных элементах.
. Эта функция изменяется линейно в пределах конечных элементов, примыкающих к 3-му узлу и тождественно равна нулю на всех остальных конечных элементах.
 |
Линейная комбинация таких функций, очевидно, представляет собой ломаную линию (см рис15).
Отметим, что при таком выборе функций 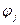 , коэффициенты
, коэффициенты  разложения (33) имеют совершенно ясный смысл:
разложения (33) имеют совершенно ясный смысл: 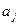 ‑ это значение приближенного решения
‑ это значение приближенного решения 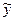 в
в 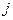 -том узле.
-том узле.
На рис.15 показано 5 аппроксимирующих функций 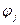 , которым соответствуют пять неизвестных коэффициентов
, которым соответствуют пять неизвестных коэффициентов 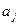 . Однако, из граничных условий
. Однако, из граничных условий 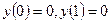 сразу следует
сразу следует 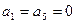 . Остается определить три неизвестных коэффициента
. Остается определить три неизвестных коэффициента 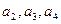 .
.
Теперь, после этих предварительных замечаний, можно приступить к построению конечно-элементных уравнений. Поскольку, как было объявлено выше, МКЭ является частным случаем метода Бубнова-Галеркина, то эти уравнения должны следовать из уравнений взвешенных невязок (32):
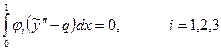 (34)
(34)
Однако, согласно (33), 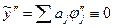 , поскольку все функции
, поскольку все функции 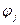 кусочно-линейные, а, значит, их вторые производные равны нулю.
кусочно-линейные, а, значит, их вторые производные равны нулю.
Возникает впечатление, что кусочно-линейные функции нельзя использовать для уравнения (1). Чтобы вторая производная 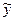 не оказалась тождественным нулем, надо использовать хотя бы квадратичные функции. Это действительно возможный путь решения, к которому мы еще вернемся.
не оказалась тождественным нулем, надо использовать хотя бы квадратичные функции. Это действительно возможный путь решения, к которому мы еще вернемся.
Однако, функции, изображенные на рис.15, выглядят очень соблазнительно из-за своей простоты. Кроме того, ломаной линией, как известно, можно с высокой точностью отобразить любую непрерывную кривую. Поэтому было бы неплохо все-таки найти способ использовать для приближенного решения именно эти функции.
Такой способ действительно имеется. Заключается он в применении метода Бубнова-Галеркина в так называемой ослабленной формулировке (см [5]). Для одномерной задачи эта процедура предельно проста. Преобразуем уравнения невязок (34), выполняя интегрирование по частям:
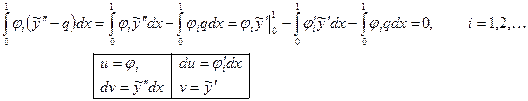 (35)
(35)
Теперь в (35) можно подставить 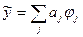 .
.
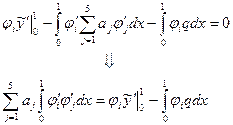 (36)
(36)
Систему уравнений взвешенных невязок (36), как обычно, представим в матричном виде:
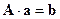 , (36)
, (36)
где
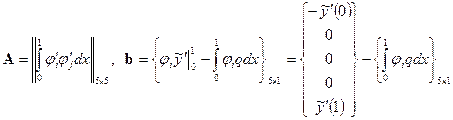 (37)
(37)
Здесь следует обратить внимание на первое слагаемое 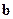 . Очевидно, что, поскольку на концах отрезка только функции
. Очевидно, что, поскольку на концах отрезка только функции 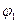 и
и 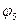 не равны нулю, то
не равны нулю, то 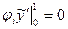 при
при  . А первая и последняя компоненты этого вектора:
. А первая и последняя компоненты этого вектора:

Еще одно важное замечание по поводу этого слагаемого. Очевидно, пока система (36) не решена, нам неизвестно ни 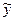 , ни, естественно,
, ни, естественно, 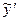 . Следовательно, первая и последняя компоненты этого вектора нам неизвестны. Однако это не мешает решению системы (36). Вспомним, что из граничных условий уже известны значения
. Следовательно, первая и последняя компоненты этого вектора нам неизвестны. Однако это не мешает решению системы (36). Вспомним, что из граничных условий уже известны значения 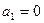 и
и 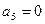 . Поэтому в системе (36) можно отбросить первое и последнее уравнения, а из оставшейся системы трех уравнений найти три неизвестных
. Поэтому в системе (36) можно отбросить первое и последнее уравнения, а из оставшейся системы трех уравнений найти три неизвестных 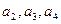 . Следует отметить, что первое и последнее уравнения (36), хотя и не понадобились при нахождении неизвестных
. Следует отметить, что первое и последнее уравнения (36), хотя и не понадобились при нахождении неизвестных 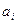 , могут принести пользу. Подставив найденные значения
, могут принести пользу. Подставив найденные значения 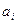 в первую и последнюю строчки (36), получим значения
в первую и последнюю строчки (36), получим значения 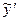 на левом и правом краях. Обычно эти значения представляют практический интерес. Так если задача (1) рассматривается как задача изгиба балки, то эти производные есть не что иное, как реакции в опорах. А если это задача о распределении температуры в стержне, то эти производные представляют потоки тепла через торцы стержня.
на левом и правом краях. Обычно эти значения представляют практический интерес. Так если задача (1) рассматривается как задача изгиба балки, то эти производные есть не что иное, как реакции в опорах. А если это задача о распределении температуры в стержне, то эти производные представляют потоки тепла через торцы стержня.
Теперь осталось вычислить значения элементов матрицы 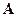 и вектора
и вектора 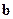 и решить систему (36). На первый взгляд единственная выгода МКЭ по сравнению с обычной схемой метода Бубнова-Галеркина состоит в том, что функции
и решить систему (36). На первый взгляд единственная выгода МКЭ по сравнению с обычной схемой метода Бубнова-Галеркина состоит в том, что функции 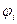 выглядят попроще, чем обычно. Однако это не так. Вся процедура построения матриц разрешающей системы (36) значительно упрощается благодаря несложному, но эффективному приему: матрицы
выглядят попроще, чем обычно. Однако это не так. Вся процедура построения матриц разрешающей системы (36) значительно упрощается благодаря несложному, но эффективному приему: матрицы 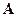 и
и 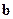 вычисляются в виде суммы интегралов. А каждый интеграл вычисляется в пределах только одного конечного элемента. То есть
вычисляются в виде суммы интегралов. А каждый интеграл вычисляется в пределах только одного конечного элемента. То есть
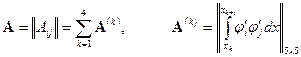 (38)
(38)
Рассмотрим особенности структуры матриц элементов на примере матрицы 2-го элемента:
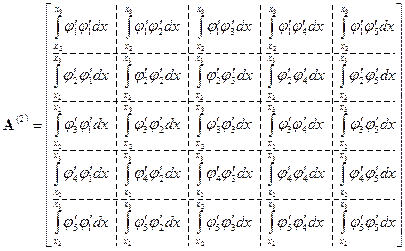
Но, как можно видеть на рис.15, в пределах второго элемента из всех функций 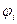 не равны нулю только две функции
не равны нулю только две функции 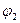 и
и  . Поэтому в матрице
. Поэтому в матрице 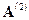 не равны нулю только четыре интеграла:
не равны нулю только четыре интеграла:
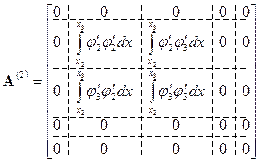 (39)
(39)
Не равные нулю элементы расположены на пересечении 2-х и 3-х строк и столбцов, то есть с номерами узлов, принадлежащих этому элементу.
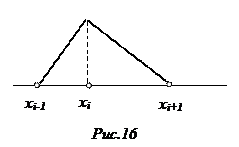 Для вычисления этих интегралов напомним, что функции
Для вычисления этих интегралов напомним, что функции 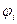 не равны нулю только в
не равны нулю только в  -том узле (см рис.16) и определятся следующим выражением:
-том узле (см рис.16) и определятся следующим выражением:
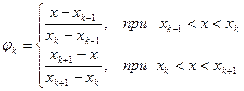 (40)
(40)
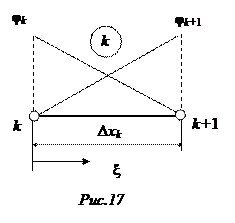 Конечный элемент с произвольным номером изображен на рисунке 17. Как это ясно из рассмотрения 2-го элемента, для
Конечный элемент с произвольным номером изображен на рисунке 17. Как это ясно из рассмотрения 2-го элемента, для 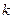 -го элемента в матрице
-го элемента в матрице 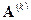 ненулевые числа будут находиться на пересечении
ненулевые числа будут находиться на пересечении 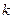 -х и
-х и 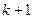 -х строк и столбцов. Таким образом, для каждого конечного элемента можно вычислить только эти числа:
-х строк и столбцов. Таким образом, для каждого конечного элемента можно вычислить только эти числа:
 (41)
(41)
Чаще всего именно эти матрицы называют матрицами конечных элементов, а матрицы вида (39) – расширенными матрицами элементов. Заметим что матрица (41) вместе с парой чисел  (номера узлов элемента) позволяют легко переписать матрицу (41) в расширенном виде.
(номера узлов элемента) позволяют легко переписать матрицу (41) в расширенном виде.
Пара чисел
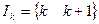 (42)
(42)
часто называется индексным вектором. Матрица элемента вместе с индексным вектором фактически представляет собой компактную запись полной (расширенной) матрицы элемента.
Получим общее выражение для матрицы (41) произвольного 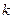 -го элемента. При вычислении интегралов удобнее перейти к безразмерной координате
-го элемента. При вычислении интегралов удобнее перейти к безразмерной координате  (см рис.17)
(см рис.17)
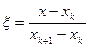 (43)
(43)
Тогда на 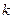 -том элементе
-том элементе
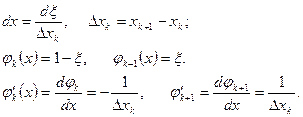
Интегралы, входящие в (41), таким образом:
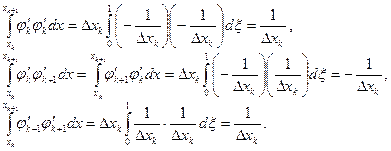
Таким образом, матрица элемента (41) для нашей задачи имеет вид:
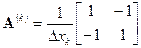 (44)
(44)
Если для решения нашей задачи (1) мы выберем одинаковые конечные элементы 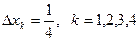 , то матрицы (41) всех элементов будут одинаковы:
, то матрицы (41) всех элементов будут одинаковы:
 ,
,
а индексные вектора:
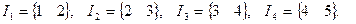
Соответствующие расширенные матрицы:
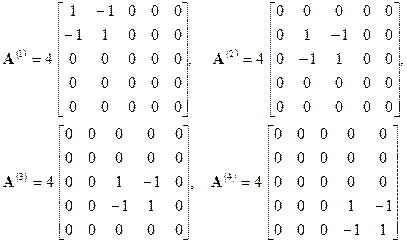
Складывая эти матрицы, в соответствии с (38), получим:
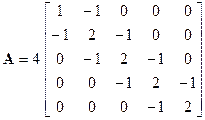
Аналогично и для вектора правых частей 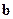 (см (37)) интегрирование удобно сначала выполнять по отдельным элементам, а полученные результаты затем сложить:
(см (37)) интегрирование удобно сначала выполнять по отдельным элементам, а полученные результаты затем сложить:
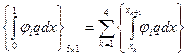
Например, для элемента № 2:

Для остальных элементов:
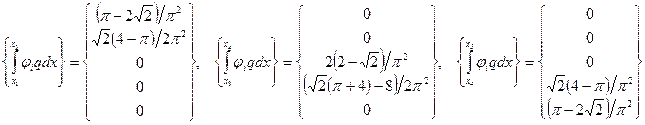 Полностью вектор
Полностью вектор 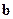 (см (37)):
(см (37)):

В развернутом виде система (36), таким образом имеет вид:
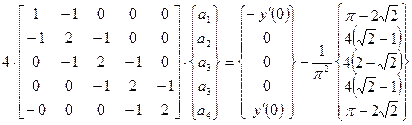
Как уже отмечалось выше, значения 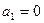 и
и 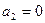 известны из граничных условий. Для определения пока неизвестных
известны из граничных условий. Для определения пока неизвестных 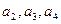 используем 2-е, 3-е и 4-е уравнения этой системы:
используем 2-е, 3-е и 4-е уравнения этой системы:
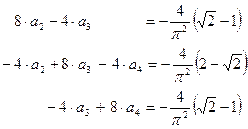
Решение этой системы:
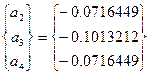
В следующей таблице приведены результаты, полученные по МКЭ с сравнении с результатами, полученными другими методами.
Таблица 7
| x | Точное решение | Метод наименьших квадратов | Метод Бубнова-Галеркина | Метод конечных элементов |
| 0.25 | -0.0716449 | -0.0717608 | -0.0717271 | -0.0716449 |
| 0.5 | -0.1013212 | -0.1010489 | -0.1012287 | -0.1013212 |
| 0.75 | -0.0716449 | -0.717608 | -0.0717271 | -0.0716449 |
Как видите, значения искомой функции в узловых точках определены без малейшей погрешности. Сразу следует предупредить, что такая сверхвысокая точность обеспечивается МКЭ только для некоторых, относительно простых видов уравнений.
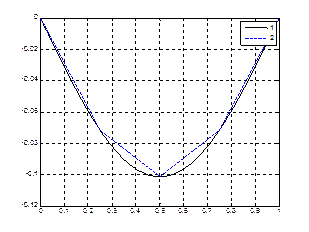 |
Кроме того напомним, что принятая система аппроксимирующих функций обеспечивает кусочно-линейную аппроксимацию (см рис.15). На рис.18 приведены графики точного (линия 1) и приближенного (линия2) решения, полученного по методу конечных элементов. Из этих графиков видно, что приближенное решение совпадает с точным в узловых точках, но в остальных точках имеется погрешность.
Рис.18
| <== предыдущая | | | следующая ==> |
| помощник редактора, редактор, главный редактор, зам. директора | | | Пожалуйста, заполните печатными заглавными буквами шариковой ручкой. |
Date: 2016-08-30; view: 489; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |