
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Плоскость в пространстве. Уравнения плоскости
Лекции 3- 4. Плоскость и прямая в пространстве
В дальнейшем полагаем, что в пространстве определена некая прямоугольная декартова система координат — каждая точка пространства однозначно определена своими координатами.
Уравнение вида  — линейное алгебраическое уравнение первой степени или просто — линейное уравнение.
— линейное алгебраическое уравнение первой степени или просто — линейное уравнение.
Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору. Пусть задана точка  и вектор
и вектор 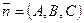 . Как отличить точки принадлежащие плоскости, проходящей через точку
. Как отличить точки принадлежащие плоскости, проходящей через точку  , перпендикулярно вектору
, перпендикулярно вектору 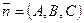 , от точек, которые этой плоскости не принадлежат?
, от точек, которые этой плоскости не принадлежат?
Можно предложить такой способ: точка 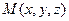 принадлежит плоскости тогда и только тогда, когда вектор
принадлежит плоскости тогда и только тогда, когда вектор 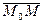 ортогонален вектору
ортогонален вектору 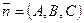 , т.е. тогда и только тогда, когда
, т.е. тогда и только тогда, когда 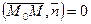 .
.
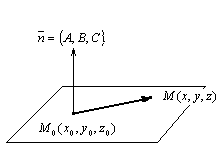
Тогда, поскольку  получим линейное уравнение
получим линейное уравнение
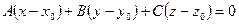 . Это уравнение плоскости, проходящей через точку
. Это уравнение плоскости, проходящей через точку  нормальным вектором
нормальным вектором 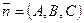 .
.
Замечание. Вектор, ортогональный плоскости, ортогонален любому вектору, принадлежащему плоскости. Такой вектор называю нормальным вектором плоскости.
Общее уравнение плоскости. Раскроем скобки в уравнении плоскости, проходящей через точку  нормальным вектором
нормальным вектором 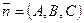 :
:  и обозначим
и обозначим 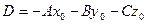 .
.
Получим общее уравнение плоскости  .
.
Из предыдущих рассуждений ясно, что коэффициенты 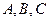 общего уравнения плоскости
общего уравнения плоскости  определяют нормальный вектор этой плоскости:
определяют нормальный вектор этой плоскости: 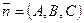 .
.
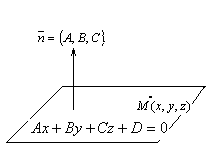
Задача (Типовой расчет!). Записать уравнение плоскости, проходящей через точку A (2, 5, -3) перпендикулярно вектору 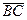 , B (7, 8, -1), C (9, 7, 4).
, B (7, 8, -1), C (9, 7, 4).
Решение. 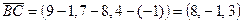 — нормальный вектор плоскости проходящей через точку A (2, 5, -3). Уравнение плоскости:
— нормальный вектор плоскости проходящей через точку A (2, 5, -3). Уравнение плоскости:  .
.
Раскрыв скобки и приведя подобные, получим искомое уравнение
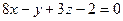 .
.
Проверим. Точка A (2, 5, -3) принадлежит плоскости: 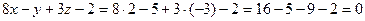 . Нормальный вектор плоскости
. Нормальный вектор плоскости 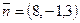 совпадает с вектором
совпадает с вектором 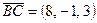 . Задача решена верно.
. Задача решена верно.
Ответ. 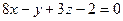 .
.
Неполные уравнения плоскости. Уравнение  определяет плоскость, проходящую через начало координат. Действительно, подставив в уравнение плоскости координаты начала координат, О (0, 0, 0), получим тождество.
определяет плоскость, проходящую через начало координат. Действительно, подставив в уравнение плоскости координаты начала координат, О (0, 0, 0), получим тождество.
Уравнение  определяет плоскость, параллельную оси 0x.
определяет плоскость, параллельную оси 0x.
Действительно, нормальный вектор этой плоскости 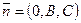 ортогонален орту оси 0x — вектору
ортогонален орту оси 0x — вектору 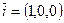 :
: 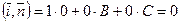 .
.
Уравнение 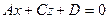 — уравнение плоскости, параллельной оси 0y, а
— уравнение плоскости, параллельной оси 0y, а
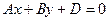 — уравнение плоскости, параллельной оси 0z.
— уравнение плоскости, параллельной оси 0z.
Уравнение 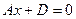 — уравнение плоскости, параллельной плоскости y0z, поскольку ее нормальный вектор
— уравнение плоскости, параллельной плоскости y0z, поскольку ее нормальный вектор 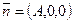 коллинеарен вектору
коллинеарен вектору 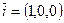 ;
;
Уравнение 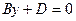 — уравнение плоскости, параллельной плоскости x0z, а уравнение
— уравнение плоскости, параллельной плоскости x0z, а уравнение 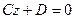 — уравнение плоскости, параллельной плоскости x0y.
— уравнение плоскости, параллельной плоскости x0y.
Нарисуйте!
Уравнение плоскости в отрезках. Рассмотрим плоскость, которая не проходит через начало координат. Ее уравнение  ,
, 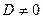 .
.
Преобразуем уравнение:  ,
, 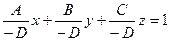 ,
, 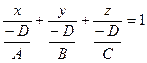 и обозначим
и обозначим 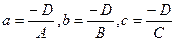 .
.
Получим уравнение 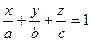 — уравнение плоскости «в отрезках».
— уравнение плоскости «в отрезках».
Плоскость, заданную таким уравнением легко рисовать. На рисунке изображен случай, когда  . Действительно, легко убедиться, что точки с координатами (a, 0,0), (0, b,0), (0,0, c) — это точки пересечения плоскости с координатными осями.
. Действительно, легко убедиться, что точки с координатами (a, 0,0), (0, b,0), (0,0, c) — это точки пересечения плоскости с координатными осями.
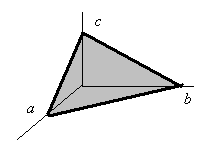
Упражнение. Изобразите сами плоскости, заданные уравнением «в отрезках» для разных сочетаний знаков коэффициентов a, b и c.
Упражнение. Рассмотрите самостоятельно вид уравнения плоскости в отрезках для неполных уравнений  ,
, 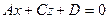 ,
, 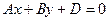 ,
, 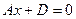 ,
, 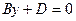 и
и 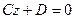 .
.
Задача. Изобразить плоскость, заданную уравнением  .
.
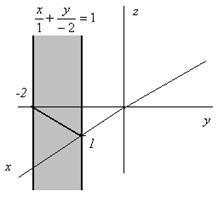
Уравнение плоскости, проходящей через три заданные точки. Известно, что три точки, не лежащие на одной прямой, однозначно определяют плоскость.
Как отличить точки принадлежащие плоскости, проходящей через точки 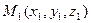 ,
, 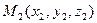 ,
, 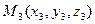 , от точек, которые этой плоскости не принадлежат? Понятно, что точка
, от точек, которые этой плоскости не принадлежат? Понятно, что точка 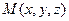 принадлежит плоскости тогда и только тогда, когда компланарны векторы
принадлежит плоскости тогда и только тогда, когда компланарны векторы 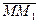 ,
, 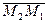 и
и 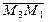 , т.е. когда
, т.е. когда 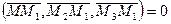 .
.
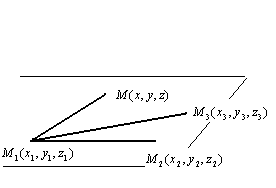
Поскольку 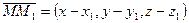 ,
, 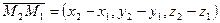 ,
, 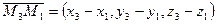 , записав смешанное произведение в координатной форме, имеем:
, записав смешанное произведение в координатной форме, имеем:
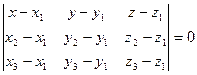 — уравнение плоскости, проходящей через три заданные точки.
— уравнение плоскости, проходящей через три заданные точки.
Преобразуем уравнение. Поскольку

получим
 — линейное уравнение первой степени.
— линейное уравнение первой степени.
Заметим, что если заданные точки лежат на одной прямой, то векторы 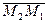 и
и 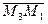 коллинеарны, т.е. все коэффициенты уравнения нулевые
коллинеарны, т.е. все коэффициенты уравнения нулевые 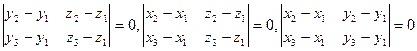 и вместо уравнения получим тождество 0 = 0.
и вместо уравнения получим тождество 0 = 0.
Нормальное уравнение плоскости. В уравнении  коэффициенты определяют нормальный вектор плоскости:
коэффициенты определяют нормальный вектор плоскости: 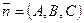 . Длина нормального вектора
. Длина нормального вектора 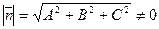 . Найдем орт нормального вектора плоскости:
. Найдем орт нормального вектора плоскости:  .
.
Легко видеть, что координаты орта вектора (орт — вектор единичной длины) равны косинусам углов, образованных этим ортом с положительными направлениями координатных осей:
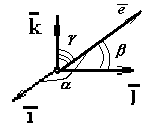
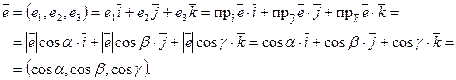
Здесь 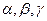 — углы, образованные ортом
— углы, образованные ортом 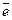 с положительными направлениями координатных осей. Косинусы этих углов называются направляющими косинусами вектора.
с положительными направлениями координатных осей. Косинусы этих углов называются направляющими косинусами вектора.
Т.е. координаты орта нормали к плоскости — направляющие косинусы нормали: 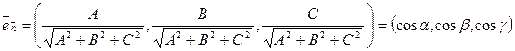 .
.
Здесь 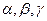 — углы, образованные нормалью к плоскостис положительными направлениями координатных осей.
— углы, образованные нормалью к плоскостис положительными направлениями координатных осей.
Разделив обе части уравнения  на
на  , получим
, получим 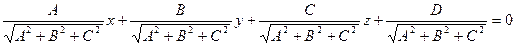 или, см. выше,
или, см. выше,
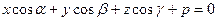 — нормальное уравнение плоскости,
— нормальное уравнение плоскости,
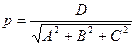 .
.
В нормальном уравнении плоскости коэффициенты при неизвестных — направляющие косинусы нормали, а свободный член p — измеряет расстояние от плоскости до начала координат. Действительно, если точка 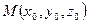 лежит на плоскости, то
лежит на плоскости, то 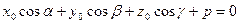 ; тогда
; тогда 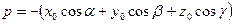 и
и 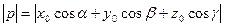 .
.
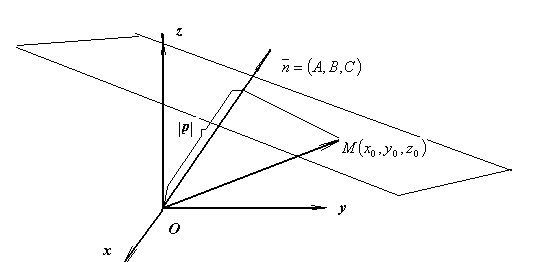
С другой стороны, расстояние от начала координат до плоскости равно, как легко видеть (см. рис.) 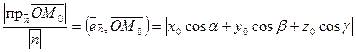 .
.
Угол между плоскостями. Угол между плоскостями равен углу между нормалями к плоскостям. Рассмотрим две плоскости, заданные уравнениями  и
и 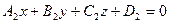 . Косинус угла между этими плоскостями легко вычислить:
. Косинус угла между этими плоскостями легко вычислить: 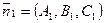 ,
, 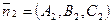 ,
, 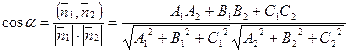 .
.
Здесь 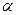 — угол между плоскостями.
— угол между плоскостями.
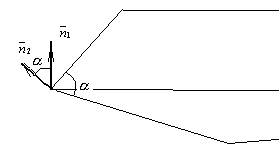
Задача (Типовой расчет!). Найти угол между плоскостями
x + 2 y – 2 z – 7=0 и x + y – 35 = 0.
Решение. 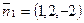 ,
, 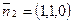 ,
, 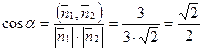 ,
, 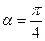 .
.
Расстояние между точкой и плоскостью.
Из приведенного рисунка видно, что расстояние от точки до плоскости равно разности длинны проекции радиуса вектора точки на орт нормали к плоскости и расстояния от начала координат до плоскости. 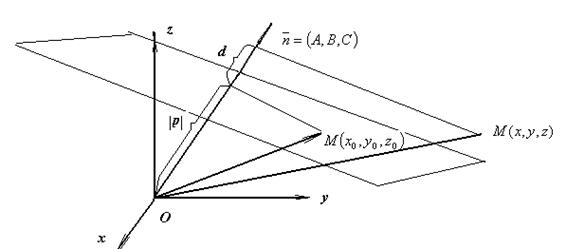
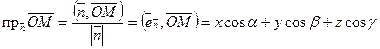 ,
, 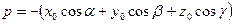 ,
,
тогда
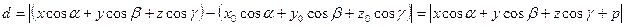 Итак, расстояние d от точки
Итак, расстояние d от точки  до плоскости
до плоскости 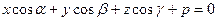
вычисляется по формуле 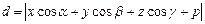 .
.
Задача. Найти расстояние от точки 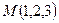 до плоскости x + y – 35 = 0.
до плоскости x + y – 35 = 0.
Решение. Запишем нормальное уравнениеплоскости x + y – 35 = 0:
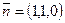 ,
,  , нормальное уравнение плоскости
, нормальное уравнение плоскости  . Тогда расстояние от точки
. Тогда расстояние от точки 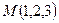 до плоскости
до плоскости  —
—

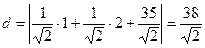 .
.
Ответ. Расстояние от точки до плоскости равно 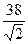 .
.
Уравнения прямой в пространстве
Общие уравнения прямой. Прямая в пространстве определяется как линия пересечения двух плоскостей. Рассмотрим две плоскости, заданные уравнениями  и
и 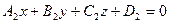 . Эти плоскости пересекаются, если их нормальные векторы не параллельны:
. Эти плоскости пересекаются, если их нормальные векторы не параллельны: 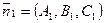 ,
, 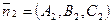 ,
, 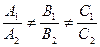 . Тогда координаты точек, принадлежащих обеим плоскостям — координаты точек прямой — удовлетворяют системе уравнений
. Тогда координаты точек, принадлежащих обеим плоскостям — координаты точек прямой — удовлетворяют системе уравнений
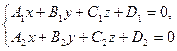 — общие уравнения прямой.
— общие уравнения прямой.
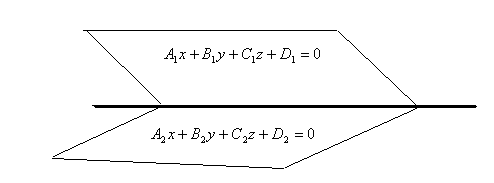
Задача. Записать общие уравнения оси 0x.
Решение. Ось 0x — линия пересечения плоскостей x0y и x0z. Уравнение плоскости x0y — z = 0, уравнение плоскости x0z — y = 0. Тогда общие уравнения оси 0x — 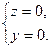
Уравнения прямой, проходящей через заданную точку параллельно заданному вектору. Пусть задана точка  и вектор
и вектор 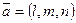 . Известно, что существует единственная прямая, проходящая через точку
. Известно, что существует единственная прямая, проходящая через точку  параллельно вектору
параллельно вектору 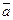 . Вектор
. Вектор 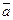 называется направляющим вектором прямой.
называется направляющим вектором прямой.
Как отличить точки принадлежащие прямой, от точек, которые этой прямой не принадлежат? Очевидно, что точка 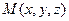 принадлежит прямой тогда и только тогда, когда векторы
принадлежит прямой тогда и только тогда, когда векторы  и
и 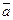 коллинеарны, т.е. когда координаты этих векторов пропорциональны;
коллинеарны, т.е. когда координаты этих векторов пропорциональны;


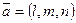 ,
,
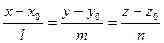 — канонические уравнения прямой, проходящей через заданную точку с заданным направляющим вектором.
— канонические уравнения прямой, проходящей через заданную точку с заданным направляющим вектором.
Задача. Записать уравнения прямой, проходящей через точку  параллельно оси 0x.
параллельно оси 0x.
Решение. Направляющий вектор прямой — это вектор 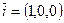 . Тогда искомые уравнения прямой —
. Тогда искомые уравнения прямой —  . Деление на нуль следует понимать так:
. Деление на нуль следует понимать так:
На нуль можно делить только числа, равные нулю, т.е. 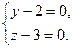
Таким образом получены не только канонические, но и общие уравнения прямой, проходящей через точку  параллельно оси 0x.
параллельно оси 0x.
Уравнения прямой, проходящей через две заданные точки. Пусть заданы две точки  и
и 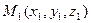 . Известно, что существует единственная прямая, проходящая через эти две точки.
. Известно, что существует единственная прямая, проходящая через эти две точки.
Как отличить точки принадлежащие прямой, от точек, которые этой прямой не принадлежат? Очевидно, что как м в предыдущей задаче, точка 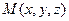 принадлежит прямой тогда и только тогда, когда векторы
принадлежит прямой тогда и только тогда, когда векторы  и
и 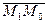 коллинеарны (в этом случае вектор
коллинеарны (в этом случае вектор 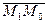 — направляющий вектор прямой), т.е. когда координаты этих векторов пропорциональны;
— направляющий вектор прямой), т.е. когда координаты этих векторов пропорциональны;

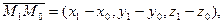
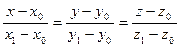 — канонические уравнения прямой, проходящей через две заданные точки.
— канонические уравнения прямой, проходящей через две заданные точки.
Параметрические уравнения прямой. Вернемся к каноническим уравнениям прямой: 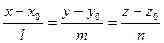 . Обозначим
. Обозначим 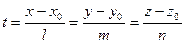 . Переменная t принимает все значения из
. Переменная t принимает все значения из 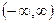 .
.
Тогда координаты точки 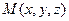 , принадлежащей прямой, удовлетворяют системе уравнений
, принадлежащей прямой, удовлетворяют системе уравнений
 — параметрические уравнения прямой, проходящей через заданную точку с заданным направляющим вектором. Здесь
— параметрические уравнения прямой, проходящей через заданную точку с заданным направляющим вектором. Здесь 
Заметим, что при t =0 получим координаты точки  .
.
Связь различных видов уравнений прямой.
Общие уравнения прямой — система двух линейных уравнений первой степени относительно трех неизвестных.
Как записать общие уравнения прямой, если известны ее канонические уравнения?
Цепочка равенств 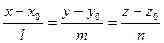 эквивалентна системе
эквивалентна системе

а это — система двух линейных уравнений первой степени относительно трех неизвестных, т.е. общие уравнения прямой.
Как записать общие уравнения прямой, если известны ее параметрические уравнения?
а это — система двух линейных уравнений первой степени относительно трех неизвестных, т.е. общие уравнения прямой.
Система  эквивалентна системе
эквивалентна системе  а это — система двух линейных уравнений первой степени относительно трех неизвестных, т.е. общие уравнения прямой.
а это — система двух линейных уравнений первой степени относительно трех неизвестных, т.е. общие уравнения прямой.
Как записать канонические уравнения прямой, если известны ее общие уравнения?
Для того чтобы записать канонические уравнения прямой, нужно найти направляющий вектор прямой и точку на прямой.
Если прямая задана общими уравнениями 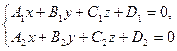 , то ее направляющий вектор ортогонален нормальным векторам обеих плоскостей:
, то ее направляющий вектор ортогонален нормальным векторам обеих плоскостей:  и
и 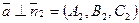 , т.е. направляющий вектор прямой можно вычислить как векторное произведение нормальных векторов:
, т.е. направляющий вектор прямой можно вычислить как векторное произведение нормальных векторов: 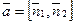 ,
, 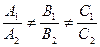 . Координаты точки на прямой можно найти как одно из множества решений системы
. Координаты точки на прямой можно найти как одно из множества решений системы 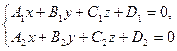 .
.
Когда точка и направляющий вектор найдены, можно записать канонические уравнения прямой.
Задача (Типовой расчет!). Записать канонические уравнения прямой 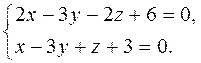
Направляющий вектор прямой ортогонален нормальным векторам обеих плоскостей:  и
и 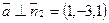 , т.е. направляющий вектор прямой можно вычислить как векторное произведение нормальных векторов:
, т.е. направляющий вектор прямой можно вычислить как векторное произведение нормальных векторов: 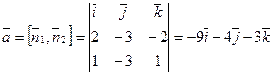 . Координаты точки на прямой можно найти как одно из множества решений системы
. Координаты точки на прямой можно найти как одно из множества решений системы 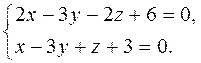
Положим 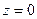 . Тогда
. Тогда 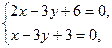
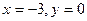 , т.е. точка (-3,0,0) лежит на искомой прямой. Теперь можно записать канонические уравнения прямой, проходящей через точку (-3,0,0) с направляющим вектором
, т.е. точка (-3,0,0) лежит на искомой прямой. Теперь можно записать канонические уравнения прямой, проходящей через точку (-3,0,0) с направляющим вектором 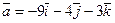 :
:
 или, что то же самое,
или, что то же самое, 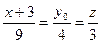 .
.
Ответ. Канонические уравнения прямой 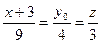 .
.
Взаимное расположение прямой и плоскости
Параллельность прямой и плоскости. Прямая 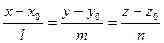 параллельна плоскости
параллельна плоскости  тогда и только тогда, когда направляющий вектор прямой
тогда и только тогда, когда направляющий вектор прямой 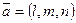 ортогонален нормальному вектору плоскости
ортогонален нормальному вектору плоскости 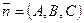 :
:
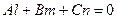 .
.
Прямая 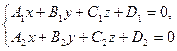 параллельна плоскости
параллельна плоскости  тогда и только тогда когда нормальные векторы
тогда и только тогда когда нормальные векторы 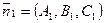 ,
, 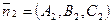 и
и 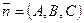 компланарны:
компланарны:
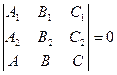 .
.
Пересечение прямой и плоскости. Если прямая и плоскость не параллельны, то они пересекаются. Точка пересечения прямой 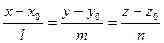 и плоскости
и плоскости  — решение системы
— решение системы
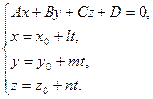
Точка пересечения прямой 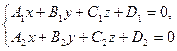 и плоскости
и плоскости  — решение системы
— решение системы 
Задача (Типовой расчет!). Найти точку пересечения прямой 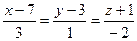 и плоскости
и плоскости 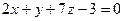 .
.
Решение. Запишем уравнения прямой в параметрической форме
 и найдем точку пересечения прямой и плоскости как решение системы
и найдем точку пересечения прямой и плоскости как решение системы  Имеем:
Имеем: 
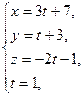
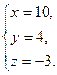
Проверим:
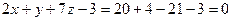 ,
,  . Верно.
. Верно.
Ответ. Точка пересечения прямой и плоскости имеет координаты (10, 4, -3).
Задача (Типовой расчет!). Найти точку, симметричную точке  относительно плоскости
относительно плоскости 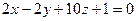 .
.
Решение.
Точка, симметричная данной относительно плоскости, лежит на перпендикуляре к плоскости и удалена от плоскости на такое же расстояние, что и заданная точка.
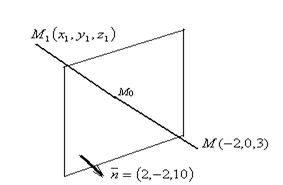
Запишем параметрические уравнения прямой, проходящей через точку M перпендикулярно плоскости 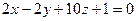 . Направляющий вектор прямой — нормальный вектор плоскости
. Направляющий вектор прямой — нормальный вектор плоскости 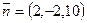 .
.
Параметрические уравнения прямой: 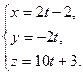
Найдем точку M 0 пересечения этой прямой и плоскости: 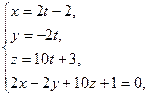
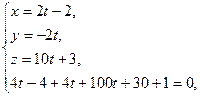
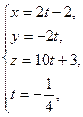

Точка 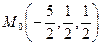 — середина отрезка
— середина отрезка 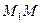 , где
, где 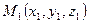 — искомая симметричная точка. Тогда
— искомая симметричная точка. Тогда 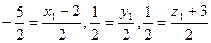 и
и 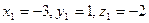 .
.
Ответ. Симметричная точка — 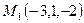 .
.
Задача (Типовой расчет!). Найти точку, симметричную точке 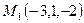 относительно прямой
относительно прямой 
Решение.
Точка, симметричная данной точке относительно прямой, лежит на плоскости, перпендикулярной прямой и удалена от прямой на такое же расстояние, что и заданная точка.
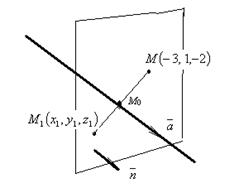
Запишем уравнение плоскости, проходящей через точку M перпендикулярно прямой 
Нормальный вектор плоскости — направляющий вектор прямой 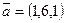 . Уравнение плоскости:
. Уравнение плоскости: 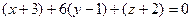 ,
, 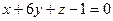 .
.
Найдем точку M 0 пересечения этой прямой и плоскости: 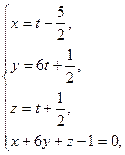
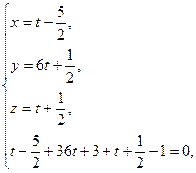
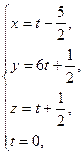

Точка 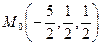 — середина отрезка
— середина отрезка 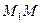 , где
, где 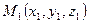 — искомая симметричная точка. Тогда
— искомая симметричная точка. Тогда 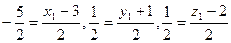 и
и  .
.
Ответ. Симметричная точка — 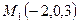 .
.
Взаимное расположение прямых
Параллельность прямых. Прямая  параллельна прямой
параллельна прямой 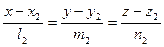 тогда и только тогда, когда их направляющие векторы коллинеарны:
тогда и только тогда, когда их направляющие векторы коллинеарны: 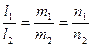 .
.
Расстояние от точки до прямой.
Из рисунка видно, что расстояние d от точки 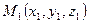 до прямой
до прямой 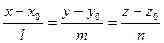 равно высоте параллелограмма, построенного на векторах
равно высоте параллелограмма, построенного на векторах 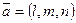 и
и 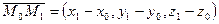 как на сторонах;
как на сторонах;  — точка на прямой.
— точка на прямой.
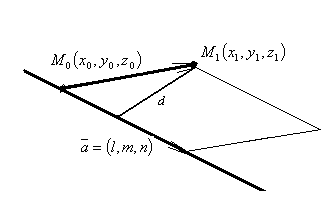
Тогда 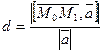 .
.
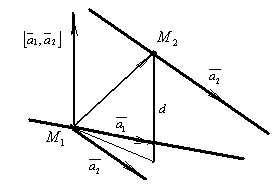
Расстояние между двумя непараллельными прямыми. Расстояние d между двумя непараллельными прямыми  и
и 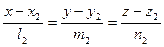 ,
, 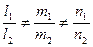 , равно проекции вектора
, равно проекции вектора  на общий перпендикуляр прямых.
на общий перпендикуляр прямых.
Общий перпендикуляр прямых коллинеарен векторному произведению их направляющих векторов: 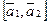 . А поскольку
. А поскольку  ,
,  и
и 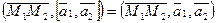 , то
, то 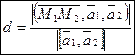 . Здесь
. Здесь 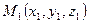 ,
, 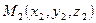 — точки на прямых,
— точки на прямых, 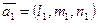 и
и  — направляющие векторы прямых.
— направляющие векторы прямых.
Задача. Найти расстояние между ребрами AC и SB тетраэдра ABCS:
A (1,0,0), B (1,3,0), C (2,7,0), S (1,1,1).
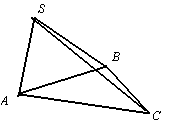
Решение. Направляющий вектор прямой, проходящей через вершины A и C — 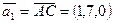 . Направляющий вектор прямой, проходящей через вершины S и B —
. Направляющий вектор прямой, проходящей через вершины S и B — 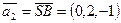 . Тогда расстояние d между ребрами AC и SB вычисляется по формуле
. Тогда расстояние d между ребрами AC и SB вычисляется по формуле 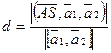 ;
;  ,
, 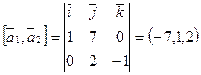 ,
, 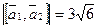 ,
, 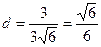 .
.
| <== предыдущая | | | следующая ==> |
| | | Всероссийская акция «Ночь искусств» 3 ноября 2016 года, 10.00 – 24.00 |
Date: 2016-11-17; view: 396; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |