ДӘРІС 1-2

Дәріс сабақтың құрылымы:

1 Дифференциалдық теңдеуге келтірілетін есептер

2 Жай дифференциалдық теңдеулер теориясы туралы негізгі ұғымдар

3 Бірінші ретті жай дифференциалдық теңдеулер

4 Айнымалысы бөлектенген теңдеулер

5 Айнымалысы бөлектенетін теңдеулер

Дәріс сабақтың мазмұны:

Зерттеліп отырған құбылысты немесе процесті сипаттайтын функцияны тікелей анықтау (табу) әлбетте, мүмкін болмайды. Алайда, тәуелсіз айнымалыны, функцияны, және олардың туындыларын байланыстыратын қатысты құрудың сәті түседі. Мұндай қатысты математикада дифференциалдық теңдеу деп атайды. Сонымен,

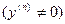, (1)

түріндегі теңдеуді (қатысты) дифференциалдық теңдеу дейміз. Дифференциалдық теңдеуге кіретін туындының ең жоғарғы реті берілген дифференциалдық теңдеудің реті деп аталады. Мысалға , тиісінше бірінші, екінші ретті дифференциалдық теңдеулер болады.

Анықтама: Белгілі бір аралықта n ретті үздіксіз дифференциалданатын функциясы (1)

теңдеуді х -ке қарағанда тепе-теңдікке айналдырса, демек болса, онда функциясы (1) теңдеудің шешімі деп аталады. Мысалға, теңдеуінің шешімі , ал 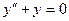теңдеуінің шешімдері немесе функциялары екені көрініп тұр. Сондай-ақ 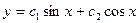функциясы екінші теңдеудің шешімі екенін көрсетіңдер. Мұнда с₁, с₂ кез келген еркін тұрақтылар.

Табиғаттану ғылымдарының, техниканың көптеген есептерін шешу дифференциалдық теңдеулерді құруға және оны шешуге келіп тіреледі.

Мысал-1. Кез келген нүктесінен жүргізілген жанаманың оу осінен қиып түсетін кесіндісінің шамасы жанасу нүктесінің екі еселенген ординатасына тең болатындай қисықтың теңдеуін тап.

	М іздеп отырған қисықтың кез келген нүктесі болсын. М(х,у) нүктесінен жүргізілген жанаманың теңдеуі түрінде анықталатыны белгілі. Мұнда X,Y жанаманың ағымдағы координаттары, -іздеп отырған функцияның берілген нүктедегі туындысы. ОВ кесіндісінің шамасын табу үшін х= 0 деп аламыз.

Сонда болады. Екінші жағынан, есептің шарты бойынша ОВ=2у. Онда 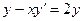немесе теңдеуі іздеп отырған дифференциалдық теңдеуіміз болып табылады. Оның шешімі у=у(х) жоғарыдағы есептің шартында көрсетілген қасиеттерге ие болатын қисықтың теңдеуі болып шығады.

Кіріспеде берілген есептердің шарты бойынша құрылған барлық дифференциалдық теңдеулерді осы курсты оқып үйрену барысында шеше алатын боласыңдар. Сөйтіп, есептерде қойылған сұрақтардың жауабын табуға да мүмкіндік туады.

F(x,y,y¹)=0 (2)

түрінде берілген теңдеуді бірінші ретті дифференциалдық теңдеу деп атайды. Егер (2) теңдеу -қа қарағанда шешілетін болса, онда оны

=f(x,y) (3)

түріне келтіруге болады. (3) теңдеуді туындыға қатысты шешілген бірінші ретті дифференциалдық теңдеу деп атайды.

Анықтама 1. Егер үздіксіз дифференциалданатын y=j(x) функциясы I интервалында (2) немесе (3) теңдеуді х - ке қарағанда тепе-теңдікке айландырса, демек F(x, j(x), (x))º0 ( (x)ºf(x, j(x))), кез келген х Î I, онда j(х) функциясын берілген (2) немесе (3) теңдеудің шешімі деп атайды.

Егер ф(х,у)=0 теңдеуі у -ті х -тің функциясы ретінде анықтайтын болса, (y=j(x)) және j(x) функциясы (3) теңдеудің шешімі болса, онда ф(х,у)=0 қатысын (3) теңдеудің айқындалмаған формадағы шешімі (интегралы) деп атайды.

Мысалы-2. А йталық теңдеуі берілсін функция y=e^х осы теңдеудің шешімі болады. Себебі

e^хlne^х –xe^х=e^хx-xe^хº0.

Алайда, берілген теңдеудің басқада шешімдері бар. Мысалы, e^-х функциясы да осы теңдеудің шешімі болады.

е^-хlne^-х-x(e^-х)¹=e^-х(-x)-xe^-х(-1)º0

Сондай-ақ е^сх түріндегі функцияларда (мұнда с -қандайда бір тұрақты) берілген теңдеудің шешімі болатының тексеруге болады.

Сонымен дифференциалдық теңдеудің бір шешімі ғана емес, көп шешімі болатынына көзімізді жеткіздік. Бұл факт, тіпті интегралдық есептеу кезінен белгілі болған. Шынында да,

(4)

қарапайым теңдеуін алсақ, бұл теңдеудің шешімі f(x) функциясының анықталмаған интегралы екені белгілі.

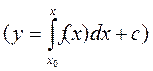
Демек, сансыз көп шешімі бар. (4) теңдеудің шешімдерінің жалпы түрін былай жазуға болады. у=j(x)+c мұнда j(х) (4) теңдеудің қандайда бір шешімі. С -ға мәндер беру арқылы (4) теңдеудің дербес шешімін табуға болады.

(3) дифференциалдық теңдеудің шешімдерінің жалпы түрін у=j(x,с) формуласы арқылы жазуға болады.

Жалпы жағдайда дифференциалдық теңдеулердің шешімдерінің жалпы түрі Ф(х,у,с)=0 формуласы арқылы жазылады. Бұл қатысты (3) теңдеудің жалпы интегралы деп атайды.

(3) теңдеудің шешімінің графигін осы теңдеудің интегралдық қисығы деп атайды. Жоғарыда айтылғандай кез келген дифференциалдық теңдеудің шешімдері ақырсыз жиын болатынын айттық. Практикада дифференциалдық теңдеудің белгілі шартты қанағаттандыратындай бір ғана шешімін табу керек болады.

(3) теңдеудің j(х₀)=у₀ (y | ) шартын қанағаттандыратын у=j(х) шешімін табуды 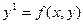теңдеуі үшін тұжырымдалған Коши есебі (немесе бастапқы есеп) дейді.

y | шартын бастапқы шарт деп атайды. х₀,_, у₀ шамаларын бастапқы берілімдер дейді.

функциясы белгілі шарттарды қанағаттандырғанда

теңдеуі үшін тұжырымдалған Коши есебінің жалғыз ғана шешімінің бар және жалғыз болатынын дәлелдеуге болады.

(5)

теңдеуін әрқашан

M(x,y)dx+N(x,y)dy (6)

түріне келтіруге болады және керісінше. Мысалға (5) теңдеуді (1.12) теңдеуге келтіру үшін оның екі жағын N(x,y)dx көбейтсек болғаны. Сонда (6) түрге келтіреміз. Бұл жағдайда M(x,y)=-f(x,y)N(x,y).

Анықтама 5. Мына түрдегі 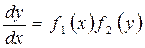(1.11^/) және M₁(x)M₂(y)dx+N₁(x)N₂(y)dy=0 (7) теңдеулерді айнымалысы ажыратылатын теңдеу деп атаймыз. (7) теңдеуіне тән қасиет dx пен dy шамаларының коэффицеттері екі функцияның көбейтіндісінен тұрады. Олардың әрқайсысы бір ғана айнымалыға тәуелді болады.

Егер болса, онда (7) теңдеуді түріне келтіреміз. Соңғы теңдеуді мына түрде жазуға болады:

Осыдан

Мұнда C еркін тұрақты. Алынған теңдеудің сол жағын F(x,y) белгілесек F(x,y)=C теңдігін аламыз. Ол берілген теңдеудің жалпы интегралы болып табылатыны белгілі.

Ал егер , онда y=y₀ функциясы (7) теңдеуінің шешімі болады. Өйткені (7) теңдеуінің dy=dy₀=0 болғандықтан екінші қосылғышы да нольге айналады. Сондай-ақ N₁,(x₀)=0, онда x=x₀ де (7) теңдеуінің шешімі болады. Дәлелдеу жоғарғыдай.

Бұл шешімдер дербес немесе ерекше шешімде бола алады. Егер көрсетілген шешімдер параметр C –ның белгілі бір мәндерінде жалпы шешімінен алынса, онда олар дербес шешімдер болады, ал қарама-қарсы жағдайда ерекше шешімге жатады.

Мысал-3.. . Бұл теңдеудің айнымалысы ажыратылған. Сондықтан интегралдау арқылы аламыз. Осыдан немесе , , мұнда немесе .

Мысал-4. Теңдеудің дербес шешімдерін тап немесе Коши есебін шеш.

Алдымен жалпы шешімді іздейміз

Берілген теңдеу айнымалысы ажыратылатын теңдеу. Онда интегралдасақ .

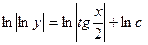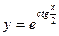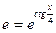Потенциалдағаннан кейін , немесе болады. Сонымен жалпы шешім табылды. Жалпы шешімнен дербес шешімді бөліп алу үшін , деп алып, демек , e=e^c c= 1 Cонда іздеп отырған дербес шешім функциясы болады.

теңдеуі айнымалысы ажыратылатын теңдеуге келтіріледі. Ол үшін ax+by+c=z деп аламыз. . ax+by+c және ауыстыру арқылы теңдеуін аламыз. Бұл теңдеу-айнымалысы ажыратылатын теңдеу. Оны интегралдау арқылы Ф(х,z,c₁)=0 теңдігіне келеміз. Енді z –ті ax+by+c өрнегімен ауыстырып Ф(х,ах+ву+с,c₁)=0 немесе F(x,y,c₁)=0 жалпы шешімі (жалпы интегралы) табылады.

Өзін-өзі тексеруге арналған сұрақтар:

1 Жай дифференциалдық теңдеулер теориясы туралы негізгі ұғымдар

2 Бірінші ретті жай дифференциалдық теңдеулер

3 Айнымалысы бөлектенетін теңдеулер

Қолданылған әдебиеттер:

1. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения.- М.: Наука, 1985

2. Қалиев С.Қ., Искакова М.Т. Дифференциалдық теңдеулер және варияциялық есептеу негіздері, Семей – 2005

3. Филлипов А.Ф. Сборник задач по обыкновенные дифференциальным уравнениям. М.: Наука, 1984

4. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. - Москва.: Изд-во МГУ, 1984.

5. Қадыкенов Б.М. Дифференциалдық теңдеулердің есептері мен жаттығулары Алматы: Қазақ университеті, 2002

Date: 2015-11-15; view: 1191; Нарушение авторских прав