Алгебра лунного перелета

Точно таким же способом, каким мы нашли точки равной слышимости двух систем громкоговорителей, можно найти и точки равного притяжения космической ракеты двумя небесными телами – Землей и Луной. Разыщем эти точки.

По закону Ньютона, сила взаимного притяжения двух тел прямо пропорциональна произведению притягивающихся масс и обратно пропорциональна квадрату расстояния между ними. Если масса Земли М, а расстояние ракеты от нее x, то сила, с какой Земля притягивает каждый грамм массы ракеты, выразится через

,

где k – сила взаимного притяжения одного грамма одним граммом на расстоянии в 1 см.

Сила, с какой Луна притягивает каждый грамм ракеты в той же точке, равна

,

где т – масса Луны, а l – ее расстояние от Земли (ракета предполагается находящейся между Землей и Луной, на прямой линии, соединяющейих центры). Задача требует, чтобы

или

.

Отношение , как известно из астрономии, приближенно равно 81,5; подставив, имеем:

,

откуда

.

Решив уравнение относительно x, получаем:

x ₁ = 0,9 l, x ₂ = 1,12 l.

Как и в задаче о громкоговорителях, мы приходим к заключению, что на линииЗемля–Луна существуют две искомые точки – две точки, где ракета должна одинаково притягиваться обоими светилами; одна на 0,9 расстояния между ними, считая от центра Земли, другая – на 1,12 того же расстояния. Так как расстояние l между центрами Земли и Луны» 384 000 км, то одна из искомых точек отстоит от центра Земли на 346 000 км, другая – на 430 000 км.

Рис. 17.

Но мы знаем (см. предыдущую задачу), что тем же свойством обладают и все точки окружности, проходящей через найденные две точки как через концы диаметра. Если будем вращать эту окружность около линии, соединяющей центры Земли и Луны, то она опишет шаровую поверхность, все точки которой будут удовлетворять требованиям задачи.

Диаметр этого шара, называемого сферой притяжения (рис. 17) Луны, равен

1,12 l – 0,9 l = 0,22 l» 84 000 км.

Распространено ошибочное мнение, будто бы для попадания ракетой в Луну достаточно попасть в ее сферу притяжения. На первый взгляд кажется, что если ракета очутится внутри сферы притяжения (обладая не слишком значительной скоростью), то она неизбежно должна будет упасть на поверхность Луны, так как сила лунного притяжения в этой области "превозмогает" силу притяжения Земли. Если бы это было так, то задача полета к Луне сильно облегчилась бы, так как надо было бы целиться не в саму Луну, поперечник которой виден на небе под углом ½° а в шар диаметром 84 000 км, угловой размер которого равняется 12°.

Однако нетрудно показать ошибочность подобных рассуждений.

Допустим, что запущенная с Земли ракета, непрерывно теряющая свою скорость из-за земного притяжения, оказалась внутри сферы притяжения Луны, имея нулевую скорость. Упадет ли она теперь на Луну? Ни в коем случае!

Во-первых, и внутри сферы притяжения Луны продолжает действовать земное притяжение. Поэтому в стороне от линии Земля – Луна сила притяжения Луны не будет просто "превозмогать" силу притяжения Земли, а сложится с ней по правилу параллелограмма сил и даст равнодействующую, направленную отнюдь не прямо к Луне (только на линии Земля – Луна эта равнодействующая была бы направлена прямо к центру Луны).

Во-вторых (и это самое главное), сама Луна не является неподвижной целью, и если мы хотим знать, как будет двигаться по отношению к ней ракета (не будет ли она на нее "падать"), то нужно учесть скорость ракеты относительно Луны. А эта скорость вовсе не равна нулю, так как сама Луна движется вокруг Земли со скоростью 1 км/сек. Поэтому скорость движения ракеты относительно Луны слишком велика для того, чтобы Луна могла притянуть к себе ракету или хотя бы удержать ее в своей сфере притяжения в качестве искусственного спутника.

Фактически притяжение Луны начинает оказывать существенное влияние на движение ракеты еще до того, как ракета приблизится к сфере притяжения Луны. В небесной баллистике принято учитывать притяжение Луны с момента, когда ракета окажется внутри так называемой сферы действия Луны радиусом 66 000 км. При этом уже можно рассматривать движение ракеты относительно Луны, полностью забывая о земном притяжении, но точно учитывая ту скорость (относительно Луны), с какой ракета входит в сферу действия. Естественно поэтому, что ракету приходится посылать к Луне по такой траектории, чтобы скорость (относительно Луны) входа в сферу действия была направлена прямо на Луну. Для этого сфера действия Луны должна набегать на ракету, движущуюся ей наперерез. Как видим, попадание в Луну оказывается вовсе не столь простым делом, как попадание в шар диаметром 84000 км.

<Paaaa

"Трудная задача"

Картина Богданова-Бельского "Трудная задача" известна многим, но мало кто из видевших эту картину

вникал в содержание той "трудной задачи", которая на ней изображена. Состоит она в том, чтобы устным счетом быстро найти результат вычисления:

.

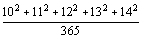Задача в самом деле нелегкая. С нею, однако, хорошо справлялись ученики того учителя, который с сохранением портретного сходства изображен на картине, именно С. А. Рачинского, профессора естественных наук, покинувшего университетскую кафедру, чтобы сделаться рядовым учителем сельской школы. Талантливый педагог культивировал в своей школе устный счет, основанный на виртуозном использовании свойств чисел. Числа 10, 11, 12, 13 и 14 обладают любопытной особенностью: .

Так как 100 + 121 + 144 = 365, то легко рассчитать в уме, что воспроизведенное на картине выражение равно 2.

Рис. 18.

Алгебра дает нам средство поставить вопрос об этой интересной особенности ряда чисел более широко: единственный ли это ряд из пяти последовательных чисел, сумма квадратов первых трех из которых равна сумме квадратов двух последних?

РЕШЕНИЕ

Обозначив первое из искомых чисел через х, имеемуравнение

x ² + (х + 1)² + (x + 2)² = (х + 3)² + (x + 4)².

Удобнее, однако, обозначить через x не первое, а второе из искомых чисел. Тогда уравнение будет иметь более простой вид

(х – 1)² + x ² + (x + 1)² = (х + 2)² + (x + 3)².

Раскрыв скобки и сделав упрощения, получаем:

x ² – 10 x – 11 = 0.

откуда

.

Существуют, следовательно, два ряда чисел, обладающих требуемым свойством: ряд Рачинского

10, 11, 12, 13, 14

и ряд

–2, –1, 0, 1, 2.

В самом деле,

(–2)² + (–1)² + 0² = 1² + 2².

<Paaaa