Формула Циолковского

Если мы проинтегрируем выведенное выше дифференциальное уравнение, то получим зависимость скорости ракеты от массы сгоревшего топлива. Результирующая формула называется идеальным уравнением реактивного движения или формулой Циолковского, который вывел ее в 1897 году.

Чтобы получить указанную формулу, удобно переписать дифференциальное уравнение в следующем виде:

Разделяя переменные и интегрируя, находим:

Заметим, что dm обозначает уменьшение массы. Поэтому, возьмем приращение dm с отрицательным знаком. В результате, уравнение принимает вид:

где v ₀ и v ₁ − начальная и конечная скорость ракеты, а m ₀ и m ₁ − начальная и конечная масса ракеты, соответственно.

Полагая v ₀ = 0, получим формулу, выведенную Циолковским:

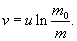
Данная формула определяет скорость ракеты в зависимости от изменения ее массы по мере сгорания топлива. С помощью этой формулы можно грубо оценить запас топлива, необходимый для ускорения ракеты до определенной скорости.

6. Динамики в неинерциальных системах отчета. Силы инерции.

1. Силы инерции при ускоренном поступательном движении системы отсчета. На тележке к штативу на нити подвешен шарик массой m (рис. 1). Пока тележка покоится или движется прямолинейно и равномерно, нить, которая удерживает шарик, занимает вертикальное положение и сила тяжести Р уравновешивается силой реакции (натяжения) нити Т.

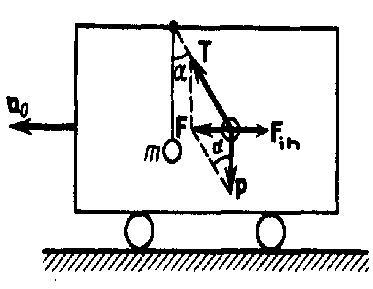
Рис.1

Если тележку привести в поступательное движение с ускорением а ₀, то нить будет отклоняться от вертикали в сторону, обратную движению, до такого угла α, пока результирующая сила F = P + T не даст ускорение шарика, равное а ₀. Значит, результирующая сила F направлена в сторону ускорения тележки а ₀ и для установившегося движения шарика (теперь шарик движется вместе с тележкой с ускорением а ₀) равна F=mgtgα=ma₀, откуда

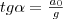
т. е. угол отклонения нити от вертикали тем больше, чем больше ускорение тележки.

В системе отсчета, которая связана с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой F _in, которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Таким образом,

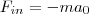(2)

Проявление сил инерции при поступательном движении мы можем видеть в повседневных явлениях. Если поезд набирает скорость, то пассажир, сидящий при этом по ходу поезда, прижимается к спинке сиденья под действием силы инерции. Наоборот, при торможении поезда пассажир отклоняется от спинки сиденья, т.к. сила инерции направлена в противоположную сторону. Особенно силы инерции заметны при внезапном торможении поезда. Эти силы проявляются в перегрузках, возникающие при запуске и торможении космических кораблей.

2. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета. Пусть диск равномерно вращается с угловой скоростью ω (ω=const) вокруг перпендикулярной ему оси, которая проходит через его центр. На диске установлены маятники, на разных расстояниях от оси вращения и на нитях висят шарики массой m. Когда диск начнет вращаться, шарики отклоняются от вертикали на некоторый угол (рис. 2).

Рис.2

В инерциальной системе отсчета, которая связана, например, с помещением, где установлен диск, происходит равномерное вращение шарика по окружности радиусом R (расстояние от центра вращающегося шарика до оси вращения). Значит, на него действует сила, равная F=mω²R и которая направлена перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести Р и силы реакции (натяжения) нити Т: F = P + T. Когда движение шарика установится, то F=mgtgα=mω²R, откуда

т. е. углы отклонения нитей маятников будут тем больше, чем больше угловая скорость вращения &omega и чем больше расстояние R от центра шарика до оси вращения диска;.

Относительно системы отсчета, которая связана с вращающимся диском, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой F_с, являющаяся ничем иным, как силой инерции, так как никакие другие силы на шарик не действуют. Сила F _c, называемая центробежной силой инерции, направлена по горизонтали от оси вращения диска и равна

(3)

На практике действие центробежных сил инерции испытывают, например, пассажиры в движущемся автобусе на поворотах, летчики при выполнении фигур высшего пилотажа; центробежные силы инерции используются во всех центробежных механизмах: насосах, сепараторах и т. д., где они достигают очень больших значений. При проектировании быстро вращающихся деталей машин (винтов самолетов, роторов и т. д.) используются специальные механизмы для уравновешивания центробежных сил инерции.

Из формулы (3) следует, что центробежная сила инерции, которая действует на тела во вращающихся системах отсчета и которая направлена в сторону радиуса от оси вращения, зависит от угловой скорости вращения ω системы отсчета и радиуса R, но при этом не зависит от скорости тела относительно вращающихся систем отсчета. Значит, центробежная сила инерции действует во вращающихся системах отсчета на все тела, которые удалены от оси вращения на конечное расстояние, при этом не имеет значения, покоятся ли они в этой системе отсчета (как мы предполагали до сих пор) или движутся относительно нее с некоторой скоростью.

3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета. Пусть шарик массой m движется с постоянной скоростью ν' вдоль радиуса равномерно вращающегося диска (ν'=const, ω=const, ν перпендикулярно ω). Если диск не начал вращаться, то шарик, движется по радиальной прямой и попадает в точку А, если же диск привести во вращение в направлении, которое указанно стрелкой, то шарик покатится по кривой OВ (рис. 3а), причем его скорость ν' относительно диска сменит свое направление. Это возможно лишь в случае, если на шарик действует сила, которая перпендикулярна скорости ν'.

Рис.3

Чтобы заставить шарик катиться по вращающемуся диску вдоль радиуса, будем использовать жестко укрепленный вдоль радиуса диска стержень, на котором шарик движется без трения прямолинейно равномерно со скоростью ν' (рис. 3б). При отклонении шарика стержень действует на него с некоторой силой F. Во вращающейся системы отсчета, т.е. относительно диска, шарик движется прямолинейно и раномерно, что объясняется тем, что сила F уравновешивается приложенной к шарику силой инерции F _k, которая перпендикулярной скорости ν'. Эта сила называется кориолисовой силой инерции.

Можно показать, что сила Кориолиса

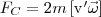
Вектор F _k перпендикулярен векторам скорости v ' тела и угловой скорости вращения системы отсчета в соответствии с правилом правого винта.

Сила Кориолиса действует только на тела, которые движутся относительно вращающейся системы отсчета, чаще всего рассматривается случай относительно Земли. Действием этих сил объясняется ряд наблюдаемых на Земле явлений. Так, если тело движется в северном полушарии на север (рис. 4), то действующая на него сила Кориолиса, как это следует из выражения (4), будет направлена вправо по отношению к направлению движения, т. е. тело несколько отклонится на восток. Если тело движется на юг, то сила Кориолиса также действует вправо, если смотреть по направлению движения, т. е. тело отклонится на запад. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые, и т. д. Также можно показать, что в южном полушарии сила Кориолиса, которая действует на движущиеся тела, направлена влево по отношению к направлению движения.

Рис.4

Благодаря действию силы Кориолиса падающие на поверхность Земли предметы отклоняются к востоку (на широте 60° это отклонение должно составлять 1 см при падении с высоты 100 м). С силой Кориолиса связано движение маятника Фуко, которое явилось в свое время одним из доказательств вращения Земли. Если бы силы Кориолиса не было, то тогда плоскость колебаний качающегося вблизи поверхности Земли маятника оставалась бы неизменной (относительно Земли). Действие же данной силы приводит к вращению плоскости колебаний вокруг вертикального направления.

Раскрывая содержание F _in в формуле (1), получим основной закон динамики для неинерциальных систем отсчета:

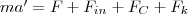
где силы инерции задаются формулами (2) - (4).

Еще раз подчеркнем, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета. По этой причине они не подчиняются третьему закону Ньютона, так как если на тело действует сила инерции, то не существует силы, противодействующей ей и приложенной к данному телу. Два основных положения механики, по которым ускорение всегда вызывается силой, а сила всегда обусловлена взаимодействием между телами, в системах отсчета, движущихся с ускорением, одновременно не выполняются.

Для любого из тел, которые находятся в неинерциальной системе отсчета, силы инерции являются внешними; Значит, здесь нет замкнутых систем, т.е. в неинерциальных системах отсчета не выполняются также и законы сохранения импульса, энергии и момента импульса. Значит, силы инерции действуют только в неинерциальных системах отсчета. В инерциальных системах отсчета таких сил не существует.

Возникает вопрос о реальном или фиктивном существовании сил инерции. В ньютоновской механике, в которой сила является результатом взаимодействия тел, на силы инерции можно смотреть как на не существующие в инерциальных системах отсчета или фиктивные. Однако возможна и другая их интерпретация. Поскольку взаимодействия тел осуществляются посредством силовых полей, то силы инерции рассматриваются как воздействия, которым подвергаются тела со стороны каких-то реальных силовых полей, и тогда их можно считать реальными. Независимо рассмотрения сил инерции в качестве реальных или фиктивных, многие явления, упоминающиеся в настоящем параграфе, объясняются с помощью сил инерции.

Силы инерции, которые действуют на тела в неинерциальной системе отсчета, пропорциональны их массам и при прочих равных условиях сообщают этим телам одинаковые ускорения. Значит в поле сил инерции эти тела движутся абсолютно одинаково, если только одинаковы начальные условия. Тем же свойством обладают тела, которые находятся под действием сил поля тяготения.

Возможны условия, при которых силы инерции и силы тяготения невозможно различить. Например, движение тел в равноускоренном лифте происходит точно так же, как и в неподвижном лифте, висящем в однородном поле тяжести. Никакой эксперимент, выполненный внутри лифта, не может отделить однородное поле сил инерции от однородного поля тяготения.

Аналогия между силами тяготения и силами инерции лежит в основе принципа эквивалентности сил инерции и гравитационных сил (принципа эквивалентности Эйнштейна): все физические явления в поле тяготения происходят так же, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а остальные начальные условия для рассматриваемых тел одинаковы. Этот принцип является основой общей теории относительности.

7. Момент инерции твердого тела. Определение и способ расчета. Теорема штейнера.

Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело

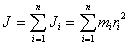
(5.4)

В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами 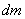, и моменты инерции тела определяется интегралом

(5.5)

о где 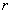- расстояние от элемента 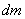до оси вращения.

Распределение массы в пределах тела можно охарактеризовать с помощью
плотности

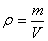
(5.5)

где m - масса однородного тела, V - его объем. Для тела с неравномерно распределенной массой это выражение даетсреднюю плотность.

Плотность в данной точке в этом случае определяется следующим образом

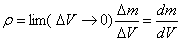
и тогда

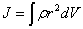
(5.6)

Пределы интегрирования зависят от формы и размеров тела Интегрирование уравнения (5.5) наиболее просто осуществить для тех случаев, когда ось вращения проходит через центр тяжести тела. Рассмотрим результаты интегрирования для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.

Момент инерции полого цилиндра с тонкими стенками, радиуса R.

Для полого цилиндра с тонкими стенками

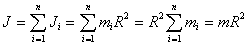
Сплошной однородный диск. Ось вращения является осью диска радиуса . и массы m с плотностью 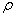Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки и массой 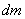. Для него

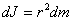
Весь диск можно разбить на бесконечное множество цилиндров, а затем просуммировать:

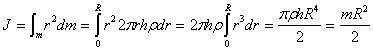
Момент инерции шара относительно оси, проходящей через центр тяжести.

Момент инерции стержня длиной L и массой m относительно оси, проходящей:

а) через центр стержня -

б) через начало стержня -

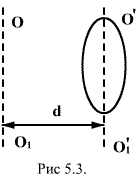
Теорема Штейнера. Имеем тело, момент инерции которого относительно оси, проходящей через его центр масс 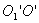известен. Необходимо определить момент инерции относительно произвольно оси 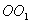параллельной оси 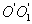. Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями:

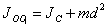
(5.7)

момент инерции 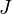тела относительно произвольной оси равен сумме момента инерции этого тела 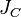относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела 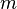на квадрат расстояния между осями:

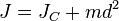
где

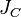— известный момент инерции относительно оси, проходящей через центр масс тела,

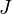— искомый момент инерции относительно параллельной оси,

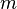— масса тела,

— расстояние между указанными осями.

8. Момент импульса материальной точки и твердого тела. Закон сохранения и изменения момента импульса.

Векторное произведение радиуса-вектора 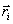материальной точки на ее импульс: называют моментом импульса 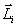, этой точки относительно точки О (рис.5.4)

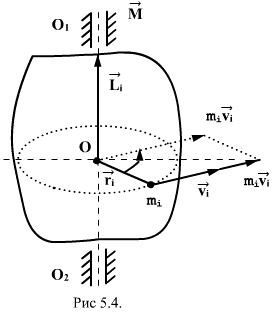
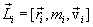. Вектор 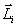иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы 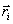и и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от 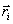к происходит против часовой стрелки).

Векторную сумму моментов импульсов 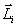всех материальных точек системы называют моментом импульса (количества движения) 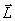системы относительно точки О:

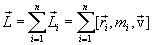
Векторы 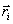и взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому . Сучетом связи линейных и угловых величин

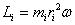
и направлен вдоль оси вращения тела в ту же сторону, что и вектор .

Таким образом.

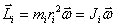
Момент импульса тела относительно оси вращения

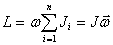
т.е.

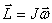
(5.9)

Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси.

Для замкнутой системы тел момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему.
Поэтому 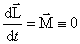, то есть

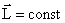или

Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.
Это один из фундаментальных законов природы.

9. Момент силы. Основной уравнение динамики вращательного движения.

Date: 2015-11-13; view: 925; Нарушение авторских прав