Задача о встрече

Пример 8. Два лица и условились встретиться в определённом месте между двумя и тремя часами дня. Пришедший первым ждет другого в течение 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?

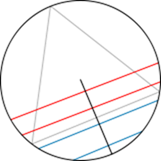
Решение. Будем считать интервал с 14 до 15 часов отрезком [0, 1] длиной в 1 час. Пусть («кси») и («эта») — моменты прихода и — точки отрезка [0, 1]. Все возможные результаты эксперимента — точки квадрата со стороной 1:

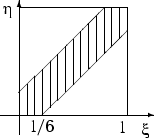
Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки множества :

(10 минут = 1/6 часа). Попадание в множество наудачу брошенной в квадрат точки означает, что и встретятся. Тогда вероятность встречи равна

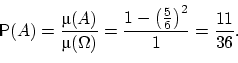
Парадокс Бертрана (вероятность)

Материал из Википедии — свободной энциклопедии

Для термина «Парадокс Бертрана» см. другие значения.

Парадокс Бертрана — проблема классического определения теории вероятностей. Жозеф Бертран описал парадокс в своей работе Calcul des probabilités (1888) в качестве примера того, что вероятность не может быть четко определена, пока не определен механизм или метод выбора случайной величины^[1].

Формулировка Бертрана

Парадокс Бертрана заключается в следующем: рассмотрим равносторонний треугольник, вписанный в окружность. Наудачу выбирается хорда окружности. Какова вероятность того, что выбранная хорда длиннее стороны треугольника?

Бертран предложил три решения, очевидно верных, но дающих различный результат.

Метод «случайных концов»: наудачу выберем две точки на окружности и проведем через них хорду. Чтобы посчитать искомую вероятность, представим, что треугольник повернут так, что одна из его вершин совпадает с концом хорды. Заметим, что если другой конец хорды лежит на дуге между двумя другими вершинами треугольника, то длина хорды больше стороны треугольника. Длина рассмотренной дуги равна трети длины окружности, следуя классическому определению, искомая вероятность равна .

Метод «случайного радиуса»: зафиксируем радиус окружности, наудачу выберем точку на радиусе. Построим хорду, перпендикулярную зафиксированному радиусу, проходящую через выбранную точку. Для нахождения искомой вероятности, представим, что треугольник повернут так, что одна из его сторон перпендикулярна зафиксированному радиусу. Хорда длиннее стороны треугольника, если ее центр ближе к центру, чем точка пересечения треугольника с зафиксированным радиусом. Сторона треугольника делит пополам радиус, следовательно вероятность выбрать хорду длиннее стороны треугольника .

Метод «случайного центра»: выберем наудачу произвольную точку внутри круга и построим хорду с центром в выбранной точке. Хорда длиннее стороны равностороннего треугольника, если выбранная точка находится внутри круга, вписанного в треугольник. Площадь вписанного круга есть 1/4 от площади большего, значит исходная вероятность равна .

10 Средние характеристики выборки

Пусть x ₁, x ₂, …, x _n– выборка из генеральной совокупности объёма n.

Выборочной средней (или средним значение выборки) называется среднее арифметическое значение признака выборочной совокупности.

Если все значения x ₁, x ₂, …, x _nпризнака выборки объема n различны, то

. (1)

Если все значения признака x ₁, x ₂, …, x _kимеют соответственно частоты n ₁, n ₂, …, n _k, причем n ₁+ n ₂+ …+ n _k= n, то

. (2)

Если дано распределение непрерывной случайной величины, то вместо x _i, берут середину интервала, т.е. .

Выборочным средним квадратичным отклонением (стандартом) называют квадратный корень из выборочной дисперсии:

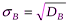. (7)

ыборка называется репрезентативной (представительной), если она в основном правильно отражает особенности генеральной совокупности.

Выборка, все члены которой записаны в виде упорядоченного, возрастающего или убывающего по своей числовой величине ряда, называется вариационным рядом.

Размахом вариационного ряда называется разность числовых значений крайних членов ряда.

Модой - М_о - называется наиболее вероятное значение случайной величины или то значение этой величины, частота которого наибольшая.

Медианой - М_е - называется такое среднее значение, которое делит совокупность всех значений случайной величины на две равные по количеству членов ряда части, причем в одной из них все значения случайной величины меньше медианы, а в другой - больше.

Для того чтобы определить медиану, необходимо расположить все члены ряда в возрастающем или убывающем порядке. При нечетном числе членов ряда n=2m +1 медиана равна М_е=Х_m+1, при четном n =2m - медиана равна

усть случайный эксперимент описывается случайной величиной X, распределение которой зависит от одного или несколько параметров. К ним, в частности, относятся среднее, мода, медиана, среднее квадратичное отклонение, дисперсия, коэффициенты эксцесса и асимметрии, размах вариации, называемые параметрами генеральной совокупности. При исследовании случайной величины X из генеральной совокупности ее возможных значений извлекается выборка объема n. По данной выборке можно приближенно вычислить значения каждого из изучаемых параметров, которые в статистике называются числовыми оценками параметров или просто оценками.

Данные характеристики условно разбиваются на четыре группы:

· показатели положения вариант на числовой оси;

· показатели разброса вариант относительно своего центра, определяющие кучность данных около центра;

· показатели асимметрии распределения вариант около своего центра;

· показатели, описывающие закон распределения.

Пусть выборка задана вариационным рядом (табл. 4).

Таблица 4. Вариационный ряд

Варианты X
Относительные частоты wi

Выборочным средним значением выборки называется число, определяемое по формуле , где x_i – варианта с частотой n_i, n – число наблюдений, . Если частоты равны единице, то k = n. При достаточно больших n используют формулу: где k – число значений вариационного ряда, w_i – относительная частота варианты x_i.

Выборочной медианой называется значение признака, находящегося в середине вариационного ряда. Если число вариант нечетно, т. е. , то медианой является ()-я варианта (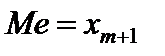); если же число вариант четно, то медиана равна среднему арифметическому двух значений в середине ряда: .

Выборочной модой (Мо) называется варианта выборки, имеющая наибольшую частоту. Если несколько соседних значений имеют наибольшую частоту, то модой является их среднее арифметическое:

, где для вариант частоты . Если две или более несмежных вариант имеют разные наибольшие частоты, то ряд называется полимодальным. Если же все варианты встречаются одинаково часто, то ряд моды не имеет.

Мода и медиана используются в качестве характеристики среднего положения в случае, если границы ряда нечеткие или если ряд не симметричен.

Для описания рассеивания значений случайной величины относительно выборочного среднего используются выборочная дисперсия и выборочное среднее квадратическое отклонение.

Выборочной дисперсией значений выборки { x ₁, x ₂,…, x_n } называется число, определяемое по формуле

.

После преобразований получается следующая формула:

.

Если задан вариационный ряд, то используется формула , где k – число вариант, w_i – относительная частота варианты .

Выборочным средним квадратическим отклонением называется число, которое находится по формуле .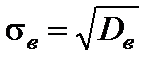

4 Множество всех действительных чисел несчетно

множество всех действительных чисел несчетно. Этот замечательный факт, как и теорема о счетности множества всех рациональных чисел, впервые в 1874 г. был доказан знаменитым немецким математиком Г. Кантором, основателем теории множеств. Воспроизводим доказательство Кантора. Доказываем, что несчетным является уже множество всех действительных чисел интервала (0; 1).

Под интервалом (а; 6) числовой прямой понимается множество всех действительных чисел х, удовлетворяющих неравенству а<x<b. Каждое такое действительное число может быть записано в виде бесконечной десятичной дроби с целой частью нуль. При этом каждому действительному числу соответствует лишь одна такая запись, за исключением действительных чисел, выражаемых конечными десятичными дробями: каждое такое число, например 0,2476622021711, может быть записано двумя способами в виде бесконечной десятичной дроби:

Одна из этих записей начиная с некоторого момента содержит одни лишь нули, а другая - одни девятки. Докажем теперь теорему о несчетности множества действительных чисел от противного: предположим, что множество действительных чисел (мы говорим все время о числах X интервала (0; 1) счетно, т. е. может быть занумеровано посредством натуральных чисел. Тогда вся совокупность действительных чисел интервала (0; 1) может быть записана в виде последовательности: х₁, x ₂ ,... Запишем разложение числа Хп в бесконечную десятичную дробь:

суть, последовательные десятичные знаки числа х _nпричем, согласно заключенному нами условию, не может случиться, что все десятичные знаки начиная с некоторого суть девятки. Итак, все действительные числа х (интервала (0; 1) предполагаются записанными в виде:

Приведем наше предположение к противоречию, найдя действительное число с, заключенное между 0 и 1 и заведомо не входящее в табл. (1). Для этого рассмотрим цифры, стоящие по диагонали в табл. (1), а именно

и выберем для каждого п натуральное число b_n, не превосходящее число 8 и отличное от числа а⁽ⁿ⁾ (например, при

полагаем

а при а⁽ⁿ⁾=8 полагаем b_n=7). Рассмотрим бесконечную десятичную дробь

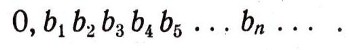
Она не содержит ни одной девятки и выражает число с, заключенное между 0 и 1, заведомо отличное от всех чисел х₁, х₂, х₃,..., х_п,... В самом деле, если бы было:

то на n-м месте в разложении числа с мы должны были бы иметь цифру а⁽ⁿ⁾ тогда как в действительности имеем

Теорема доказана.