Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Динамические расчеты стержневых систем

Стр 1 из 2Следующая ⇒




При расчетах конструкций на устойчивость используем уравнение (5.1), в котором матрица жесткости вычисляется так же как при статическом расчете.

Матрица масс для отдельного конечного элемента (Рис.5.15)

,

где 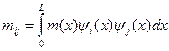(5.16)

компонент матрицы масс конечного элемента. Функции определены формулами (5.5).

Вычисляя по (5.16), (5.5), при 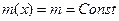, получаем матрицу масс стержневого конечного элемента:

. (5.17)

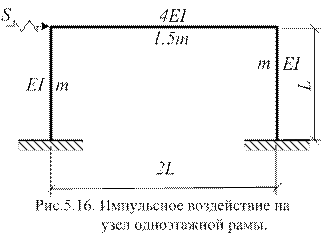Для примера рассмотрим решение динамического расчета одноэтажной рамы на действие горизонтального импульса S, приложенного в левом узле (рис.5.16).

Расчетная схема принята в виде трех конечных элементов (смотри рис.5.17): левая стойка, ригель и правая стойка. Неизвестными считаем: горизонтальное перемещение ригеля Z1, угол поворота лево го Z2 и угол поворота правого узла Z3 рамы.

С помощью (5.7), вычисляются элементы матрицы жесткости K. Элементы матрицы масс вычисляются с помощью (5.17):

При вычислении элемента m11 матрицы масс учтена масса ригеля рамы:

как масса тела, перемещаемого горизонтально.

,

, , , , .

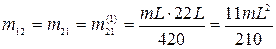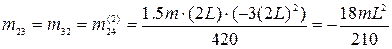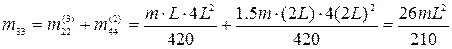Таким образом, матрица масс для системы показанной на рис.5.16:

.

Матрица жесткости определяется формулой (5.9)

.

Уравнение движения системы без учета затухания колебаний и внутренних сил статического сжатия получаем из (5.1):

. (5.18)

К решению уравнения (5.18) применим метод разложения по собственным формам. Ищем

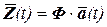, (5.19)

где - матрица собственных векторов, отвечающая условию ортогональности

, (5.20)

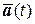- вектор коэффициентов, зависящих от времени. Отметим, что метод разложения по собственным формам изложен в разделе 4. настоящего пособия. Здесь отличие состоит в том, что вместо вектора перемещений мы имеем дело с вектором обобщенными перемещениями и вместо диагональной матрицы масс m имеем недиагональную, симметричную матрицу m. Тем не менее, кратко изложим решение нашей задачи.

Подставим (5.19) в (5.18) и умножим результат на матрицу слева, получим:

,

учитывая (5.20) и

, (5.21)

где - диагональная матрица собственных чисел, получаем

, (5.22)

где

Записав (5.22) в обычной, а не в матричной форме, получаем

, (5.23)

систему независимых обыкновенных дифференциальных уравнений относительно коэффициентов .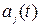

Решение уравнения (5.23) для случая

(, ),

- дельта-функция Дирака, имеет вид:

, t > 0 (5.24)

и называется импульсной переходной функцией (ИПФ) для консервативной системы, .

Решение уравнения (5.22) при произвольном bj(t) выражается интегралом Дюамеля:

. (5.25)

В матричной форме выражение (5.25) примет вид:

, (5.26)

где , f(t) – функция времени,

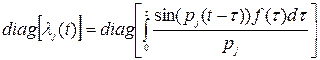
- диагональная матрица.

После подстановки (5.26) в (5.19) получаем

. (5.27)

Выражение (5.27) дает решение задачи, если известны матрицы собственных векторов Ф и матрица собственных чисел . Для их определения служат уравнения (5.20) и (5.21).

В разделе 1.3 предложен метод итераций для определения всех собственных чисел и всех собственных векторов некоторой симметричной матрицы А. Проблема сводится к решению уравнений:

, . (5.28)

Приведем уравнения (5.20), (5.21) к виду (5.28)

,

,

где , , . (5.29)

Полученные выражения имеют вид (5.28):

,

и их можно решить методом итераций.

Решение (5.27) преобразуем с помощью (5.29), получим:

.

Упростим полученное выражение. Рассмотрим произведение матриц:

.

Обозначим

, (5.30)

и назовем эту матрицу парциальная матрица собственных форм.

Решение (5.27) можно записать в виде:

. (5.31)

Итак, необходимо найти все собственные числа и собственные векторы матрицы , но предварительно необходимо найти функцию матрицы масс: .

В разделе 1.4 функции матриц определены следующим образом:

 

,

 

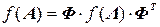где Ф – матрица собственных векторов и - матрица собственных чисел матрицы . В нашем случае роль А играет матрица m.

Находим матрицу собственных чисел , и матрицу собственных векторов матрицы m после чего вычисляем

 

.

 

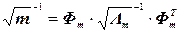По формуле (5.29) вычисляем и находим собственные векторы , собственные числа 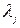и парциальные матрицы .

Решение задачи выражается формулой (5.31)

 

,

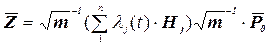или

.

 

, (5.32)

 

Обозначим , тогда с учетом (5.32):

 

.

 

Для определения расчетных изгибающих моментов воспользуемся единичной матрицей изгибающих моментов (смотри стр.6), полученной от , j= 1, 2, 3:

Расчетные изгибающие моменты определяются как

.

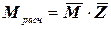Описанный выше расчет легко реализуется с помощью программного пакета Maple:

> restart;

Исходные данные:

> mm:=200.:L:=3.:

> with(LinearAlgebra):

> m:=Matrix(3,3,mm*L/210*[[786,11*L,11*L],[11*L,26*L^2,-18*L^2],[11*L,-18*L^2,26*L^2]],datatype=float[4]);

 

Вычисление собственных векторов матрицы m:

> Fi:=Matrix(3,3,Eigenvectors(m,output=vectors),datatype=float[4]);

> LL:=Matrix(3,1,Eigenvectors(m,output=values),datatype=float[4]);

> lambdaM:=Matrix(3,3,[[LL[1,1],0,0],[0,LL[2,1],0],[0,0,LL[3,1]]],datatype=float[4]);

Квадратный корень из матрицысобтвенных чисел матрицы m:

> lambdaM05:=Matrix(3,3,[[sqrt(lambdaM[1,1]),0,0],[0,sqrt(lambdaM[2,2]),0],[0,0,sqrt(lambdaM[3,3])]],datatype=float[4]);

Квадратный корень из матрицы m:

> m05:=Fi.lambdaM05.Transpose(Fi);

Квадратный корень из обратной матрицы m:

> m_05:=Matrix(3,3,m05^(-1),datatype=float[4]);

Жесткость EI:

> EI:=2.*10^11*5010.*10^(-8):

Матрица жесткости рамы:

> K:=Matrix(3,3,2*EI/(L^3)*[[12,3*L,3*L],[3*L,6*L^2,2*L^2],[3*L,2*L^2,6*L^2]],datatype=float[4]);

Матрица Km:

> Km:=Matrix(3,3,m_05.K.m_05,datatype=float[4]);

Матрица собственных векторов матрицы Km:

> Fi:=Matrix(3,3,Eigenvectors(Km,output=vectors),datatype=float[4]);

Собственные числа матрицы Km:

> LL:=Matrix(3,1,Eigenvectors(Km,output=values),datatype=float[4]);

Собственные частоты:

> p1:=sqrt(LL[1,1])/(2*Pi);

> p3:=sqrt(LL[2,1])/(2*Pi);

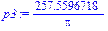
> p2:=sqrt(LL[3,1])/(2*Pi);

Собственные векторы:

> Psi1:=Matrix(3,1,Fi.Matrix(3,1,[[1],[0],[0]],datatype=float[4]));

> Psi3:=Matrix(3,1,Fi.Matrix(3,1,[[0],[1],[0]],datatype=float[4]));

> Psi2:=Matrix(3,1,Fi.Matrix(3,1,[[0],[0],[1]],datatype=float[4]));

Парциальные матрицы:

> H1:=Matrix(3,3,Psi1.Transpose(Psi1),datatype=float[4]);

> H2:=Matrix(3,3,Psi2.Transpose(Psi2),datatype=float[4]);

> H3:=Matrix(3,3,Psi3.Transpose(Psi3),datatype=float[4]);

 

Ø Az1:=m_05.H1.m_05.Matrix(3,1,[[S0],[0],[0]]);

 

Ø Az2:=m_05.H2.m_05.Matrix(3,1,[[S0],[0],[0]]);

 

Ø Az3:=m_05.H3.m_05.Matrix(3,1,[[S0],[0],[0]]);

 

Матрица изгибающих моментов от единичнх неизвестных Zi=1:

> MM:=Matrix(6,3,[[6*EI/L^2,2*EI/L,0],[-6*EI/L^2,-4*EI/L,0],[0,-8*EI/L,-4*EI/L],[0,4*EI/L,8*EI/L],[-6*EI/L^2,0,-4*EI/L],[6*EI/L^2,0,2*EI/L]]);

Значение импульса Sо:

> S0:=1;

Перемещения

> Z:=Az1*sin(2*Pi*p1*t)/(2*Pi*p1)+Az2*sin(2*Pi*p2*t)/(2*Pi*p2)+Az3*sin(2*Pi*p3*t)/(2*Pi*p3);

Матрица расчетных изгибающих моментов:

> Mpac:=MM.Z;

Графики изгибающих моментов в сечениях 2 и 3:

> plot(Mpac[2,1],t=0..0.5);

 

> plot(Mpac[3,1],t=0..0.5);

Итак, задача о действии горизонтального единичного импульса на левый верхний узел одноэтажной рамы, решена. Но при расчете мы пренебрегли диссипативными силами и сжатием стоек рамы. Для учета диссипативных сил в уравнение движения рамы введем диссипативный член: , получим

, (5.33)

где Г – диссипативная матрица.

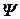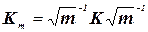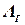Для того чтобы применить к уравнению (5.33) метод разложения по собственным формам необходимо, чтобы матрица Г имела те же самые собственные векторы , что и матрицы m и K, то есть матрица . Это значит, что , где - диагональная матрица. В качестве такой матрицы может быть принята любая функция матрицы : 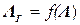. Поскольку собственные числа матрицы представляют собой квадраты собственных частот колебаний p, то 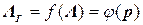. Представим 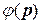в виде разложения в ряд Маклорена:

,

Сохраним в этом разложении первый ненулевой член, т.е. примем

.

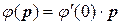Постоянную величину 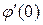обозначим , тогда

. (5.34)

Применим к уравнению (5.33) способ разложения по собственным формам, ищем решение уравнения в виде:

. (5.35)

После подстановки (5.35) в (5.33), умножения слева на матрицу получим:

,

но , , , и приняв по (5.34) , получим , где . В обычном (не в матричном) виде уравнения выглядят так:

, . (5.36)

Решение уравнения (5.36) выразим через интеграл Дюамеля

,

где импульсная переходная функция диссипативной системы или решение уравнения (5.36) при . Это решение имеет вид

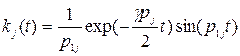, (5.37)

где . При , что справедливо для большинства конструкционных материалов, можно считать и

. (5.38)

Вычислив логарифмический декремент колебаний для функции (5.38), получим , то есть независящий от частоты p декремент колебаний.

Вычислим интеграл Дюамеля, используя (5.37) и тот факт, что нагрузка на систему :

Функция .

Решение задачи дается формулой (5.35)

,

то есть имеет и вид (5.27), в котором при вычислении функций используется ИПФ для диссипативной системы (5.38).

Найдем решение той же самой задачи о горизонтальном импульсном воздействии на узел одноэтажной рамы. Материал конструкции обладает коэффициентом потерь .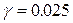

Расчет выполним, используя программу Maple:

> restart;

Исходные данные:

> S0:=1: mm:=200.:L:=3.: gam:=0.025:

> with(LinearAlgebra):

> m:=Matrix(3,3,mm*L/210*[[786,11*L,11*L],[11*L,26*L^2,-18*L^2],[11*L,-18*L^2,26*L^2]],datatype=float[4]):

Вычисление собственных векторов матрицы m:

> Fi:=Matrix(3,3,Eigenvectors(m,output=vectors),datatype=float[4]):

Вычисление собственных чисел матрицы m:

> LL:=Matrix(3,1,Eigenvectors(m,output=values),datatype=float[4:

Матрица собственных чисел матрицы m:

> lambdaM:=Matrix(3,3,[[LL[1,1],0,0],[0,LL[2,1],0],[0,0,LL[3,1]]],datatype=float[4]):

Квадратный корень из матрицысобтвенных чисел матрицы m:

> lambdaM05:=Matrix(3,3,[[sqrt(lambdaM[1,1]),0,0],[0,sqrt(lambdaM[2,2]),0],[0,0,sqrt(lambdaM[3,3])]],datatype=float[4]):

Квадратный корень из матрицы m:

> m05:=Fi.lambdaM05.Transpose(Fi):

Квадратный корень из обратной матрицы m -1 :

m_05:=Matrix(3,3,m05^(-1),datatype=float[4]):

Жесткость EI:

> EI:=2.*10^11*5010.*10^(-8):

Матрица жесткости рамы:

> K:=Matrix(3,3,2*EI/(L^3)*[[12,3*L,3*L],[3*L,6*L^2,2*L^2],[3*L,2*L^2,6*L^2]],datatype=float[4]):

Матрица Km:

> Km:=Matrix(3,3,m_05.K.m_05,datatype=float[4]):

Матрица собственных векторов матрицы Km:

> Fi:=Matrix(3,3,Eigenvectors(Km,output=vectors),datatype=float[4]):

Собственные числа матрицы Km:

> LL:=Matrix(3,1,Eigenvectors(Km,output=values),datatype=float[4]):

Собственные частоты:

> p1:=sqrt(LL[1,1])/(2*Pi):

> p3:=sqrt(LL[2,1])/(2*Pi):

> p2:=sqrt(LL[3,1])/(2*Pi):

Собственные векторы:

> Psi1:=Matrix(3,1,Fi.Matrix(3,1,[[1],[0],[0]],datatype=float[4])):

> Psi3:=Matrix(3,1,Fi.Matrix(3,1,[[0],[1],[0]],datatype=float[4])):

> Psi2:=Matrix(3,1,Fi.Matrix(3,1,[[0],[0],[1]],datatype=float[4])):

Парциальные матрицы:

> H1:=Matrix(3,3,Psi1.Transpose(Psi1),datatype=float[4]):

> H2:=Matrix(3,3,Psi2.Transpose(Psi2),datatype=float[4]):

> H3:=Matrix(3,3,Psi3.Transpose(Psi3),datatype=float[4]):

Амплитуды форм колебаний неизвестных:

> Az1:=m_05.H1.m_05.Matrix(3,1,[[S0],[0],[0]]):

> Az2:=m_05.H2.m_05.Matrix(3,1,[[S0],[0],[0]]):

> Az3:=m_05.H3.m_05.Matrix(3,1,[[S0],[0],[0]]):

Матрица изгибающих моментов от единичнх неизвестных Zi=1:

> MM:=Matrix(6,3,[[6*EI/L^2,2*EI/L,0],[-6*EI/L^2,-4*EI/L,0],[0,-8*EI/L,-4*EI/L],[0,4*EI/L,8*EI/L],[-6*EI/L^2,0,-4*EI/L],[6*EI/L^2,0,2*EI/L]]):

Перемещения:

> Z:=Az1*exp(-gam*Pi*p1*t)*sin(2*Pi*p1*t)/(2*Pi*p1)+Az2*exp(-gam*Pi*p2*t)*sin(2*Pi*p2*t)/(2*Pi*p2)+Az3*exp(-gam*Pi*p3*t)*sin(2*Pi*p3*t)/(2*Pi*p3):

Матрица расчетных изгибающих моментов:

> Mpac:=MM.Z:

Графики изгибающих моментов в сечениях 2 и 3:

> plot(Mpac,t=0..0.5);

> plot(Z,t=0..0.5);

При принятых предпосылках учета внутреннего трения, сложность решение задач для диссипативной и консервативной систем практически не различима. Отличие лишь в виде импульсных переходных функций, используемых в расчетах: по (5.24) - для консервативных и по (5.38) - для диссипативных систем. Предпосылки были сделаны для упрощения расчета, но многочисленные эксперименты с конструкционными материалами в лабораторных условиях и экспериментальные исследования строительных конструкций, установили факт частотной независимости декремента колебаний. И именно в принятой для расчетов модели демпфирования колебаний, прослеживается четкая частотная независимость декремента колебаний (). Кроме того, факт учета именно частотно независимого внутреннего трения отражен в СНиПах.

Рассмотрим пример (Рис.5.19). В отличии от предыдущего примера, нагрузкой кроме горизонтального импульса, действующего на левый узел рамы, является вертикальная узловая сжимающая нагрузка в виде двух сил N. Силы примем достаточно большими, такими, что по сравнению с ними массовую нагрузку можно не учитывать в статическом расчете. Примем величину этих сил равную значению критического параметра, полученного в примере расчета этой же рамы на устойчивость (смотри рис.5.13). Итак, положим . В динамическом расчете будем учитывать геометрическую жесткость при формировании исходного уравнения движения, т.е. используем уравнение движения (5.1). Матрицы K, m, Г были рассмотрены в предыдущем примере. Получим матрицу геометрической жесткости KG. Матрица геометрической жесткости вычисляется так же как при статическом расчете и расчете на устойчивость сложением жесткостей конечных элементов. Расчетная схема задачи приведена на рис.5.20.

 

Матрицу геометрической жесткости для рамы формируем с помощью (5.11):

 

Согласно рис.5.20 элементы матрицы геометрической жесткости получим в виде:

, , ,

, , ,

, , .

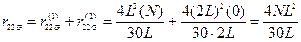Матрица геометрической жесткости будет иметь вид:

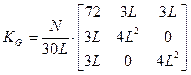. (5.39)

После подстановки принятого значения в (5.39) присваиваем новое значение матрице жесткости:

.

Далее решение задачи точно следует решению предыдущего примера. Расчет выполним на ПЭВМ, используя программный пакет Maple:

> restart;

Исходные данные:

> EI:=2.*10^11*5010.*10^(-8): S0:=1: mm:=200.: g:=9.81: L:=3.: N:=5.67397743*EI/L^2: gam:=0.025:

> with(LinearAlgebra):

> m:=Matrix(3,3,mm*L/210*[[786,11*L,11*L],[11*L,26*L^2,-18*L^2],[11*L,-18*L^2,26*L^2]],datatype=float[4]):

Вычисление собственных векторов матрицы m:

> Fi:=Matrix(3,3,Eigenvectors(m,output=vectors),datatype=float[4]):

Вычисление собственных чисел матрицы m:

> LL:=Matrix(3,1,Eigenvectors(m,output=values),datatype=float[4]):

Матрица собственных чисел матрицы m:

> lambdaM:=Matrix(3,3,[[LL[1,1],0,0],[0,LL[2,1],0],[0,0,LL[3,1]]],datatype=float[4]):

Квадратный корень из матрицысобтвенных чисел матрицы m:

> lambdaM05:=Matrix(3,3,[[sqrt(lambdaM[1,1]),0,0],[0,sqrt(lambdaM[2,2]),0],[0,0,sqrt(lambdaM[3,3])]],datatype=float[4]):

Квадратный корень из матрицы m:

> m05:=Fi.lambdaM05.Transpose(Fi):

Квадратный корень из обратной матрицы m-1:

> m_05:=Matrix(3,3,m05^(-1),datatype=float[4]):

Жесткость EI:

> EI:=2.*10^11*5010.*10^(-8):

Матрица жесткости рамы:

> K:=Matrix(3,3,2*EI/(L^3)*[[12,3*L,3*L],[3*L,6*L^2,2*L^2],[3*L,2*L^2,6*L^2]],datatype=float[4]);

Матрица геометрической жесткости:

> KG:=Matrix(3,3,N/(30*L)*[[72,3*L,3*L],[3*L,4*L^2,0],[3*L,0,4*L^2]],datatype=float[4]);

> K:=K-KG;

Матрица Km:

> Km:=Matrix(3,3,m_05.K.m_05,datatype=float[4]);

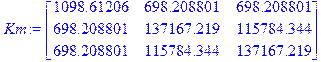
Матрица собственных векторов матрицы Km:

> Fi:=Matrix(3,3,Eigenvectors(Km,output=vectors),datatype=float[4]);

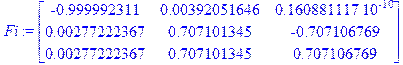
Собственные числа матрицы Km:

> LL:=Matrix(3,1,Eigenvectors(Km,output=values),datatype=float[4]):

Собственные частоты:

> p1:=sqrt(LL[1,1]);

> p3:=sqrt(LL[2,1]);

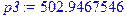
> p2:=sqrt(LL[3,1]);

Собственные векторы:

> Psi1:=Matrix(3,1,Fi.Matrix(3,1,[[1],[0],[0]],datatype=float[4]));

 

 

> Psi3:=Matrix(3,1,Fi.Matrix(3,1,[[0],[1],[0]],datatype=float[4]));

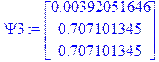
> Psi2:=Matrix(3,1,Fi.Matrix(3,1,[[0],[0],[1]],datatype=float[4]));

 

Парциальные матрицы:

> H1:=Matrix(3,3,Psi1.Transpose(Psi1),datatype=float[4]):

> H2:=Matrix(3,3,Psi2.Transpose(Psi2),datatype=float[4]):

> H3:=Matrix(3,3,Psi3.Transpose(Psi3),datatype=float[4]):

Амплитуды форм колебаний неизвестных:

> Az1:=m_05.H1.m_05.Matrix(3,1,[[S0],[0],[0]]):

> Az2:=m_05.H2.m_05.Matrix(3,1,[[S0],[0],[0]]):

> Az3:=m_05.H3.m_05.Matrix(3,1,[[S0],[0],[0]]):

Матрица изгибающих моментов от единичных неизвестных Zi=1:

> MM:=Matrix(6,3,[[6*EI/L^2,2*EI/L,0],[-6*EI/L^2,-4*EI/L,0],[0,-8*EI/L,-4*EI/L],[0,4*EI/L,8*EI/L],[-6*EI/L^2,0,-4*EI/L],[6*EI/L^2,0,2*EI/L]]):

Перемещения

> Z:=Az1*exp(-gam*p1*t/2)*sin(p1*t)/(p1)+Az2*exp(-gam*p2*t/2.)*sin(p2*t)/(p2)+Az3*exp(-gam*p3*t/2.)*sin(p3*t)/(p3):

Матрица расчетных изгибающих моментов:

> Mpac:=MM.Z:

Графики изгибающих моментов в сечениях рамы:

> plot(Mpac,t=0..0.5);

Графики перемещений рамы:

> plot(Z,t=0..0.5);

 

Сравним результаты расчета без учета и с учетом сжимающих сил. Для удобства анализа графики обобщенных перемещений и изгибающих моментов приведены на рис.5.21 и 5.22. Из этих графиков видно, что перемещения и внутренние усилия при учете сжатия примерно в два раза выше, чем аналогичные значения для рам без учета сжимающих сил. Правда, сжатие стоек принято значительным: сравнимым по порядку с критическим параметром для этой рамы.

Собственные частоты для рам с учетом сжатия отличаются от собственных частот рам без учета сжатия. Особенно сильно различаются низшие частоты, так первые частоты для рам без учета сжатия p1=57рад/сек и p1=33рад/сек для рам с учетом сжатия. Это говорит о том, что сжатием при расчете рам с сильно сжатыми элементами пренебрегать нельзя. То же самое можно сказать и о конструкциях с сильно растянутыми элементами.

Мы рассмотрели нагрузку в виде мгновенного импульса. При этом воздействии очень просто вычисляется интеграл Дюамеля. В других случаях вычисление этого интеграла еще лет 10 – 15 назад могло поставить в тупик

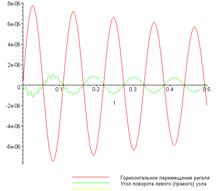
Рис.5.21. Результаты расчета рамы без учета сжатия стоек

 

Рис.5.22. Результаты расчета рамы с сильно сжатыми стойками

 

многих расчетчиков, но в настоящее время при оснащении расчетчика современными ПК и программным обеспечением типа Maple, об этой проблеме можно забыть и спокойно браться за динамический расчет на любые воздействия. Учет поглощения энергии не в состоянии создать трудностей в расчете, поскольку, отпали трудности с вычислением интеграла Дюамеля и в расчетах строительных конструкций используется известная импульсная переходная функция, определяемая формулой (5.38).

Еще раз запишем решение уравнения движения (5.1):

.

Обозначим

, (5.40)

где - амплитуда по формам колебаний:

. (5.41)

Формулу (5.41) мы уже использовали в программе расчета на импульсные воздействия. В расчетах приведенных ниже будем использовать и формулу (5.40), в которой вычисляем через интеграл Дюамеля:

,

где f(t) – функция нагрузки, определяемая из выражения .

Для примера, рассмотрим расчет той же одноэтажной рамы, загруженной динамической нагрузкой, создаваемой электродвигателем с неуравновешенным ротором, например, электродвигателем вентилятора, установленного на крыше здания, вблизи опорной стойки рамы. Расчетная схема показана на рис.5.23.

Нагрузка на раму принята в виде горизонтальной силы с амплитудой , где m0 – неуравновешенная масса, e0 – эксцентриситет неуравновешенной массы, - круговая частота вращения двигателя.

Частоту вращения будем считать переменной, т.е. нагрузка не будет гармонической. Примем следующий закон изменения нагрузки: в промежутке времени 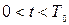частота вращения двигателя равномерно нарастает ; в промежутке времени частота вращения двигателя остается постоянной, равной , где - рабочая частота вращения; и в промежутке времени частота вращения двигателя равномерно убывает .

График, зависимости угловой скорости вращения вала двигателя от времени, приведен на рис.5.24. Закон изменения нагрузки при :

,

при :

,

при :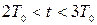

.

Обозначим - амплитуду возмущающей силы в рабочем режиме, тогда , где:

при ,

при ,

при .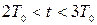

Проведем вычисления с помощью программного пакета Maple:

при разгоне двигателя

> restart;

Исходные данные:

> S0:=1.: mm:=200.;L:=3.; P0:=3000.; T0:=1.; omega_r:=104.6; gam:=0.025;

> with(LinearAlgebra):

> m:=Matrix(3,3,mm*L/210*[[786,11*L,11*L],[11*L,26*L^2,-18*L^2],[11*L,-18*L^2,26*L^2]],datatype=float[4]);

Вычисление собственных векторов матрицы m:

> Fi:=Matrix(3,3,Eigenvectors(m,output=vectors),datatype=float[4]):

Вычисление собственных чисел матрицы m:

> LL:=Matrix(3,1,Eigenvectors(m,output=values),datatype=float[4]):

Матрица собственных чисел матрицы m:

> lambdaM:=Matrix(3,3,[[LL[1,1],0,0],[0,LL[2,1],0],[0,0,LL[3,1]]],datatype=float[4]):

Квадратный корень из матрицысобственных чисел матрицы m:

> lambdaM05:=Matrix(3,3,[[sqrt(lambdaM[1,1]),0,0],[0,sqrt(lambdaM[2,2]),0],[0,0,sqrt(lambdaM[3,3])]],datatype=float[4]):

Квадратный корень из матрицы m:

> m05:=Fi.lambdaM05.Transpose(Fi):

Квадратный корень из обратной матрицы m:

> m_05:=Matrix(3,3,m05^(-1),datatype=float[4]);

Жесткость EI:

> EI:=2.*10^11*5010.*10^(-8):

Матрица жесткости рамы:

> K:=Matrix(3,3,2*EI/(L^3)*[[12,3*L,3*L],[3*L,6*L^2,2*L^2],[3*L,2*L^2,6*L^2]],datatype=float[4]);

Матрица Km:

> Km:=Matrix(3,3,m_05.K.m_05,datatype=float[4]);

Матрица собственных векторов матрицы Km:

> Fi:=Matrix(3,3,Eigenvectors(Km,output=vectors),datatype=float[4]);

Собственные числа матрицы Km:

> LL:=Matrix(3,1,Eigenvectors(Km,output=values),datatype=float[4]);

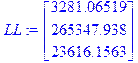
Собственные частоты:

> p1:=sqrt(LL[1,1]);

> p3:=sqrt(LL[2,1]);

> p2:=sqrt(LL[3,1]);

Собственные векторы:

> Psi1:=Matrix(3,1,Fi.Matrix(3,1,[[1],[0],[0]],datatype=float[4]));

> Psi3:=Matrix(3,1,Fi.Matrix(3,1,[[0],[1],[0]],datatype=float[4]));

> Psi2:=Matrix(3,1,Fi.Matrix(3,1,[[0],[0],[1]],datatype=float[4]));

Парциальные матрицы:

> H1:=Matrix(3,3,Psi1.Transpose(Psi1),datatype=float[4]);

> H2:=Matrix(3,3,Psi2.Transpose(Psi2),datatype=float[4]);

> H3:=Matrix(3,3,Psi3.Transpose(Psi3),datatype=float[4]);

Амплитуды форм колебаний неизвестных:

> Az1:=m_05.H1.m_05.Matrix(3,1,[[1.],[0],[0]]);

> Az2:=m_05.H2.m_05.Matrix(3,1,[[1.],[0],[0]]);

> Az3:=m_05.H3.m_05.Matrix(3,1,[[1.],[0],[0]]);

Интегралы Дюамеля :

> L1(t):=P0/(p1*T0^2)*Int(exp(-gam*p1*(t-x)/2)*sin(p1*(t-x))*sin(omega_r*x^2/T0)*x^2,x=0..t):

> L2(t):=P0/(p2*T0^2)*Int(exp(-gam*p2*(t-x)/2)*sin(p2*(t-x))*sin(omega_r*x^2/T0)*x^2,x=0..t):

> L3(t):=P0/(p3*T0^2)*Int(exp(-gam*p3*(t-x)/2)*sin(p3*(t-x))*sin(omega_r*x^2/T0)*x^2,x=0..t):

Матрица изгибающих моментов от единичных неизвестных Zi=1:

> MM:=Matrix(6,3,[[6*EI/L^2,2*EI/L,0],[-6*EI/L^2,-4*EI/L,0],[0,-8*EI/L,-4*EI/L],[0,4*EI/L,8*EI/L],[-6*EI/L^2,0,-4*EI/L],[6*EI/L^2,0,2*EI/L]]):

Перемещения:

> Z:=Az1*L1(t)+Az2*L2(t)+Az3*L3(t):

Матрица расчетных изгибающих моментов:

> Mpac:=MM.Z:

Графики изгибающих моментов в сечениях рамы Mpac:

> plot(Mpac,t=0..T0);

 

График обобщенных перемещений Zi:

> plot(Z,t=0..T0);

 

при стационарном загружении

> restart;

Исходные данные:

> S0:=1.: mm:=200.: L:=3.: P0:=3000.: T0:=1.: omega_r:=104.6: gam:=0.025:

> with(LinearAlgebra):

> m:=Matrix(3,3,mm*L/210*[[786,11*L,11*L],[11*L,26*L^2,-18*L^2],[11*L,-18*L^2,26*L^2]],datatype=float[4]):

Вычисление собственных векторов матрицы m:

> Fi:=Matrix(3,3,Eigenvectors(m,output=vectors),datatype=float[4]):

Вычисление собственных чисел матрицы m:

> LL:=Matrix(3,1,Eigenvectors(m,output=values),datatype=float[4]):

Матрица собственных чисел матрицы m:

> lambdaM:=Matrix(3,3,[[LL[1,1],0,0],[0,LL[2,1],0],[0,0,LL[3,1]]],datatype=float[4]):

Квадратный корень из матрицысобтвенных чисел матрицы m:

> lambdaM05:=Matrix(3,3,[[sqrt(lambdaM[1,1]),0,0],[0,sqrt(lambdaM[2,2]),0],[0,0,sqrt(lambdaM[3,3])]],datatype=float[4]):

Квадратный корень из матрицы m:

> m05:=Fi.lambdaM05.Transpose(Fi):

Квадратный корень из обратной матрицы m:

> m_05:=Matrix(3,3,m05^(-1),datatype=float[4]):

Жесткость EI:

> EI:=2.*10^11*5010.*10^(-8):

Матрица жесткости рамы:

> K:=Matrix(3,3,2*EI/(L^3)*[[12,3*L,3*L],[3*L,6*L^2,2*L^2],[3*L,2*L^2,6*L^2]],datatype=float[4]):

Матрица Km:

> Km:=Matrix(3,3,m_05.K.m_05,datatype=float[4]):

Матрица собственных векторов матрицы Km:

> Fi:=Matrix(3,3,Eigenvectors(Km,output=vectors),datatype=float[4]):

Собственные числа матрицы Km:

> LL:=Matrix(3,1,Eigenvectors(Km,output=values),datatype=float[4]):

Собственные частоты:

> p1:=sqrt(LL[1,1]):

> p3:=sqrt(LL[2,1]):

> p2:=sqrt(LL[3,1]):

Собственные векторы:

> Psi1:=Matrix(3,1,Fi.Matrix(3,1,[[1],[0],[0]],datatype=float[4])):

> Psi3:=Matrix(3,1,Fi.Matrix(3,1,[[0],[1],[0]],datatype=float[4])):

> Psi2:=Matrix(3,1,Fi.Matrix(3,1,[[0],[0],[1]],datatype=float[4])):

Парциальные матрицы:

> H1:=Matrix(3,3,Psi1.Transpose(Psi1),datatype=float[4]):

> H2:=Matrix(3,3,Psi2.Transpose(Psi2),datatype=float[4]):

> H3:=Matrix(3,3,Psi3.Transpose(Psi3),datatype=float[4]):

Амплитуды форм колебаний неизвестных:

> Az1:=m_05.H1.m_05.Matrix(3,1,[[1.],[0],[0]]):

> Az2:=m_05.H2.m_05.Matrix(3,1,[[1.],[0],[0]]):

> Az3:=m_05.H3.m_05.Matrix(3,1,[[1],[0],[0]]):

> L1(t):=P0/(p1*T0^2)*Int(exp(-gam*p1*(t-x)/2)*sin(p1*(t-x))*sin(omega_r*x^2/T0)*x^2,x=0..T0)+P0/(p1)*Int(exp(-gam*p1*(t-x)/2)*sin(p1*(t-x))*sin(omega_r*x),x=T0..t):

> L2(t):=P0/(p2*T0^2)*Int(exp(-gam*p2*(t-x)/2)*sin(p2*(t-x))*sin(omega_r*x^2/T0)*x^2,x=0..T0)+P0/(p2)*Int(exp(-gam*p2*(t-x)/2)*sin(p2*(t-x))*sin(omega_r*x),x=T0..t):

> L3(t):=P0/(p3*T0^2)*Int(exp(-gam*p3*(t-x)/2)*sin(p3*(t-x))*sin(omega_r*x^2/T0)*x^2,x=0..T0)+P0/(p3)*Int(exp(-gam*p3*(t-x)/2)*sin(p3*(t-x))*sin(omega_r*x),x=T0..t):

Матрица изгибающих моментов от единичнх неизвестных Zi=1:

> MM:=Matrix(6,3,[[6*EI/L^2,2*EI/L,0],[-6*EI/L^2,-4*EI/L,0],[0,-8*EI/L,-4*EI/L],[0,4*EI/L,8*EI/L],[-6*EI/L^2,0,-4*EI/L],[6*EI/L^2,0,2*EI/L]]):

Перемещения:

> Z:=Az1*L1(t)+Az2*L2(t)+Az3*L3(t):

Матрица расчетных изгибающих моментов:

> Mpac:=MM.Z:

Графики изгибающих моментов в сечениях рамы Mpac:

> plot(Mpac,t=T0..2*T0);

График обобщенных перемещений Zi:

> plot(Z,t=T0..2*T0);

 

при торможении двигателя

> restart;

Исходные данные:

> S0:=1.: mm:=200.: L:=3.: P0:=3000.: T0:=1.: omega_r:=104.6: gam:=0.025:

> with(LinearAlgebra):

> m:=Matrix(3,3,mm*L/210*[[786,11*L,11*L],[11*L,26*L^2,-18*L^2],[11*L,-18*L^2,26*L^2]],datatype=float[4]):

Вычисление собственных векторов матрицы m:

> Fi:=Matrix(3,3,Eigenvectors(m,output=vectors),datatype=float[4]):

Вычисление собственных чисел матрицы m:

> LL:=Matrix(3,1,Eigenvectors(m,output=values),datatype=float[4]):

Матрица собственных чисел матрицы m:

> lambdaM:=Matrix(3,3,[[LL[1,1],0,0],[0,LL[2,1],0],[0,0,LL[3,1]]],datatype=float[4]):

Квадратный корень из матрицысобтвенных чисел матрицы m:

> lambdaM05:=Matrix(3,3,[[sqrt(lambdaM[1,1]),0,0],[0,sqrt(lambdaM[2,2]),0],[0,0,sqrt(lambdaM[3,3])]],datatype=float[4]):

Квадратный корень из матрицы m:

> m05:=Fi.lambdaM05.Transpose(Fi):

Квадратный корень из обратной матрицы m:

> m_05:=Matrix(3,3,m05^(-1),datatype=float[4]):

Жесткость EI:

> EI:=2.*10^11*5010.*10^(-8):

Матрица жесткости рамы:

> K:=Matrix(3,3,2*EI/(L^3)*[[12,3*L,3*L],[3*L,6*L^2,2*L^2],[3*L,2*L^2,6*L^2]],datatype=float[4]):

Матрица Km:

> Km:=Matrix(3,3,m_05.K.m_05,datatype=float[4]):

Матрица собственных векторов матрицы Km:

> Fi:=Matrix(3,3,Eigenvectors(Km,output=vectors),datatype=float[4]):

Собственные числа матрицы Km:

> LL:=Matrix(3,1,Eigenvectors(Km,output=values),datatype=float[4]):

Собственные частоты:

> p1:=sqrt(LL[1,1]):

> p3:=sqrt(LL[2,1]):

> p2:=sqrt(LL[3,1]):

Собственные векторы:

> Psi1:=Matrix(3,1,Fi.Matrix(3,1,[[1],[0],[0]],datatype=float[4])):

> Psi3:=Matrix(3,1,Fi.Matrix(3,1,[[0],[1],[0]],datatype=float[4])):

> Psi2:=Matrix(3,1,Fi.Matrix(3,1,[[0],[0],[1]],datatype=float[4])):

Парциальные матрицы:

> H1:=Matrix(3,3,Psi1.Transpose(Psi1),datatype=float[4]):

> H2:=Matrix(3,3,Psi2.Transpose(Psi2),datatype=float[4]):

> H3:=Matrix(3,3,Psi3.Transpose(Psi3),datatype=float[4]):

Амплитуды форм колебаний неизвестных:

> Az1:=m_05.H1.m_05.Matrix(3,1,[[1],[0],[0]]):

> Az2:=m_05.H2.m_05.Matrix(3,1,[[1],[0],[0]]):

> Az3:=m_05.H3.m_05.Matrix(3,1,[[1],[0],[0]]):

Интегралы Дюамеля :

> L1(t):=P0/(p1*T0^2)*Int(exp(-gam*p1*(t-x)/2)*sin(p1*(t-x))*sin(omega_r*x^2/T0)*x^2,x=0..T0)+P0/(p1)*Int(exp(-gam*p1*(t-x)/2)*sin(p1*(t-x))*sin(omega_r*x),x=T0..2*T0)+P0/(p1*T0^2)*Int(exp(-gam*p1*(t-x)/2)*sin(p1*(t-x))*sin(omega_r*x*(3*T0-x)/T0)*(3*T0-x)^2,x=2*T0..t):

> L2(t):=P0/(p2*T0^2)*Int(exp(-gam*p2*(t-x)/2)*sin(p2*(t-x))*sin(omega_r*x^2/T0)*x^2,x=0..T0)+P0/(p2)*Int(exp(-gam*p2*(t-x)/2)*sin(p2*(t-x))*sin(omega_r*x),x=T0..2*T0)+P0/(p2*T0^2)*Int(exp(-gam*p2*(t-x)/2)*sin(p2*(t-x))*sin(omega_r*x*(3*T0-x)/T0)*(3*T0-x)^2,x=2*T0..t):

> L3(t):=P0/(p3*T0^2)*Int(exp(-gam*p3*(t-x)/2)*sin(p3*(t-x))*sin(omega_r*x^2/T0)*x^2,x=0..T0)+P0/(p3)*Int(exp(-gam*p3*(t-x)/2)*sin(p3*(t-x))*sin(omega_r*x),x=T0..2*T0)+P0/(p3*T0^2)*Int(exp(-gam*p3*(t-x)/2)*sin(p3*(t-x))*sin(omega_r*x*(3*T0-x)/T0)*(3*T0-x)^2,x=2*T0..t):

Матрица изгибающих моментов от единичных неизвестных Zi=1:

> MM:=Matrix(6,3,[[6*EI/L^2,2*EI/L,0],[-6*EI/L^2,-4*EI/L,0],[0,-8*EI/L,-4*EI/L],[0,4*EI/L,8*EI/L],[-6*EI/L^2,0,-4*EI/L],[6*EI/L^2,0,2*EI/L]]):

Перемещения:

> Z:=Az1*L1(t)+Az2*L2(t)+Az3*L3(t):

Матрица расчетных изгибающих моментов:

> Mpac:=MM.Z:

Графики изгибающих моментов в сечениях рамы Mpac:

> plot(Mpac,t=2*T0..3*T0);

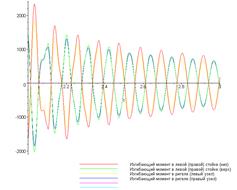
График обобщенных перемещений Zi:

> plot(Z,t=2*T0..3*T0);

Для анализа результатов расчетов покажем все графики на одном рис.5.25

 

Изгибающие моменты в сечениях рамы

 

при разгоне двигателя в стационарном режиме работы при торможении двигателя

 

 

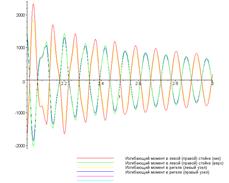
Перемещения узлов рамы

 

при разгоне двигателя в стационарном режиме работы при торможении двигателя

 

 

Рис.5.25. Результаты расчета рамы в переходных режимах работы

 

Из этих графиков видно, что наибольшие усилия и перемещения достигаются при переходе двигателя с режима разгона в стационарный режим и из стационарного режима в режим торможения. Именно и эти моменты внутренние усилия и перемещения достигают наибольших величин.

 

Рассмотрим стационарные колебания конструкций под действием гармонической нагрузки

. (5.42)

Стационарные колебания это колебания конструкций, происходящие в моменты времени после полного затухания свободных колебаний, то есть силы действуют очень долго и мы вправе искать решение уравнения (5.1) без учета свободных колебаний. Решение уравнения (5.1) при нагрузке (5.42) ищем в виде:

. (5.43)

После подстановки (5.43) в (5.1) после сокращения на получим:

. (5.44)

К решению последнего уравнения применим метод разложения по собственным формам. Решение ищем и виде:

. (5.45)

После подстановки (5.45) в (5.44), умножения слева на ФТ получаем:

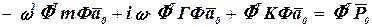, (5.46)

но, если Ф есть собственные формы отвечающие зависимостям

(5.47)

а .

Для частотно-независимого демпфирования по (5.34) принимаем

.

После подстановки (5.34) в (5.47), а затем в (5.46) получаем

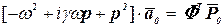. (5.48)

Поскольку матрица частот диагональная, то матрицы 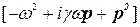и обратная ей матрица тоже диагональные. Обозначим

(5.49)

и назовем её передаточной матрицей. Диагональные, ненулевые элементы этой матрицы

-

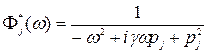комплексные величины, представляющие собой передаточные функции по соответствующим формам.

Из (5.48) с учетом (5.49) получаем

 

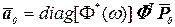. (5.50)

После подстановки (5.50) в (5.45) находим:

. (5.51)

Учитывая, что

,

, (5.52)

где -

амплитуды по формам.

Для примера рассмотрим раму, показанную на рис.5.23, при действии горизонтальной, гармонической силы 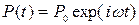. Найдем амплитуды перемещений узлов и амплитуды изгибающих моментов в сечениях 1 – 6,

Расчет выполним, используя программный пакет Maple.

> restart;

Исходные данные: mm - распределенная масса в H/м, L - размер в м (высота стойки), P0 - амплитуда нагрузки kH, gam - коэффициет потерь.

> mm:=200.: L:=3.: P0:=3000.: gam:=0.025:

> with(LinearAlgebra): <

12Следующая ⇒

Date: 2015-12-10; view: 418; Нарушение авторских прав; Помощь в написании работы --> СЮДА...


mydocx.ru - 2015-2024 year. (0.006 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию