Прямая в пространстве

Прямая в пространстве задается тремя способами.

1. Общие уравнения прямой (прямая задана как линия пересечения двух плоскостей):

1. Канонические уравнения прямой (прямая проходит через точку

параллельно вектору . Вектор называется

направляющим вектором прямой):

1. Параметрические уравнения прямой. (прямая задается как траектория движения

точки):

Здесь любое число, называемое параметром.

Пример. Задана прямая общими уравнениями

Плоскости и не параллельны, так как нормали не параллельны , значит, пересекаясь, задают прямую.

Пример. Задана прямая каноническими уравнениями

Точка лежит на этой прямой, вектор параллелен этой прямой и называется направляющим вектором.

Пример. Задана прямая параметрическими уравнениями

Направляющий вектор этой прямой . Для любого значения параметра соответствует одна точка, лежащая на прямой. Например, для получаем точку с координатами , или .

Обратно, для любой точки, лежащей на данной прямой, найдется единственное значение параметра, соответствующее этой точке. Например, точке соответствует параметр .

Пример. Найти угол между прямыми

и

Угол между прямыми – это угол между их направляющими векторами. Найдем направляющий вектор первой прямой:

- нормаль к первой плоскости,

- нормаль ко второй плоскости. Тогда направляющий вектор

Точно так же для второй прямой:

- нормаль к первой плоскости,

- нормаль ко второй плоскости. Тогда направляющий вектор

Находим косинус угла между прямыми:

Пример. Прямая задана общими уравнениями:

Получить канонические уравнения этой прямой.

Направляющий вектор прямой найден в предыдущем примере . Остается найти какую-либо точку, лежащую на прямой.

Пусть, например, , тогда решаем систему уравнений

Канонические уравнения имеют вид:

Задание 3. В пространстве заданы две прямые и .

a. Записать канонические уравнения прямой .

b. Найти угол между прямыми и .

Канонические уравнения прямой получены в предыдущем примере, направляющий вектор этой прямой . Направляющий вектор второй прямой . С помощью скалярного произведения найдем косинус угла между прямыми:

Задание 4. Составить уравнение плоскости, проходящей через три заданные точки А, В, С. Найти точку пересечения полученной плоскости с заданной прямой .

Составим уравнение плоскости, используя уравнение .

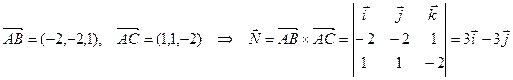
Значит, вектор нормали , или можно взять . Выбираем точку, лежащую в плоскости, например, :

В полученном уравнении отсутствует , значит, эта плоскость параллельна оси .

Найдем точку пересечения А плоскости и прямой. Для этого канонические уравнения прямой запишем в параметрическом виде:

Полученные параметрические уравнения подставим в уравнение плоскости и найдем то значение параметра , которое соответствует точке пересечения А.

Чтобы найти координаты точки пересечения, подставим в параметрические уравнения прямой и получим

Значит, .

Поверхности второго порядка.

1. Эллипсоид - поверхность, которая задается уравнением

Это уравнение называется канонически.

2. Однополостный гиперболоид - поверхность, которая задается уравнением

Это уравнение называется каноническим.

3. Двуполостный гиперболоид - поверхность, которая задается уравнением

Это уравнение называется каноническим.

4. Конус второго порядка -поверхность, которая задается уравнением

Это уравнение называется каноническим.

5. Эллиптический параболоид - поверхность, которая задается уравнением

Это уравнение называется каноническим.

6. Гиперболический параболоид - поверхность, которая задается уравнением

Это уравнение называется каноническим.

7. Эллиптический цилиндр - поверхность, которая задается уравнением

Это уравнение называется каноническим.

8. Гиперболический цилиндр - поверхность, которая задается уравнением

Это уравнение называется каноническим.

9. Параболический цилиндр - поверхность, которая задается уравнением

Это уравнение называется каноническим.

Все эти поверхности расположены относительно системы координат специальным образом. Например, центр эллипсоида находится в начале координат, а его оси являются координатными осями. Если же поверхность, не поворачивая, сместить в некоторую точку, ее каноническое уравнение изменится. Чтобы узнать, куда было сделано смещение и распознать поверхность, надо выделить полные квадраты.

Задание 5. Получить каноническое уравнение, указать название поверхности.

Выделим полные квадраты:

Это двуполостный гиперболоид, с центром в точке с осью, параллельной оси

Date: 2015-12-10; view: 401; Нарушение авторских прав