Аналитическая геометрия

Уравнения прямой на плоскости.

Пусть дано уравнение: F (x, y) = 0. Если числа x0,y0 при подстановке в уравнение дают верное равенство, то говорят, что пара чисел x0,y0 удовлетворяет данному уравнению. Например, пара x0 =10,y0 = 9 удовлетворяет уравнению 1 – х + у = 0, а пара x1 =2,y1 =3 – не удовлетворяет. Пара чисел x и y, удовлетворяющих данному уравнению, не может быть какой угодно: если x задано, то y нельзя выбрать произвольно, значение y связано с x.Но отсюда следует, что если мы будем изменять значение x, то будет как-то меняться и значение y.Точка (x,y) на координатной плоскости при этом будет описывать некоторую линию.

Иначе говоря, если дано уравнение и ставится задача найти линию, определяемую этим уравнением, то нужно собрать все точки (x,y), координаты которых удовлетворяют данному уравнению. Обратно: если дана какая-то линия и нужно написать её уравнение, то следует подобрать такое уравнение с двумя переменными, чтобы ему удовлетворяли координаты всех точек, лежащих на данной линии, и только таких точек.

Если известно уравнение некоторой линии, то исследование геометрических свойств этой линии сводится к исследованию её уравнения – в этом заключается одна из основных идей аналитической геометрии. Её ценность состоит в том, что исследование уравнения, как правило, проще, чем непосредственное геометрическое исследование линии, тем более что для исследования уравнений имеются хорошо разработанные методы алгебры и математического анализа.

Задача о пересечении двух линий.

Пусть линии l 1 и l 2 заданы своими уравнениями F(х, у) =0 (уравнение l 1), Ф(х, у) =0 (уравнение l 2). Найдём точки пересечения этих линий. С позиций аналитической геометрии «найти точки пересечения» означает, что по отношению к заданной системе координат нужно определить координаты точек пересечения.

Пусть М (x0,y0) – одна из точек пересечения. Тогда F(x0,y0) = 0, т.к. точка М лежит на l 1,но в тоже время Ф (x0,y0) = 0, т.к. точка М лежит на l 2. Значит, числа x0,y0 удовлетворяют системе уравнений

Обратно, если пара чисел x0,y0 удовлетворяет этой системе, то точка М(x0,y0) принадлежит одновременно обеим линиям, т.е. является их точкой пересечения.

Если система не имеет решения, то линии не пересекаются; если имеется одно решение (т.е. единственная пара чисел x0,y0), то существует только одна точка пересечения; если таких решений несколько, это означает, что линии пересекаются в нескольких точках.

Прямая на плоскости и её уравнение.

Положение прямой на плоскости можно характеризовать различными способами. Например, можно задать:

а) две точки М0 и М1,через которые должна проходить прямая;

б) одну из точек М0 и вектор ā, которому должна быть параллельна прямая;

в) одну из точек М0 и вектор , которому должна быть перпендикулярна прямая;

г) одну из точек М0 и угол φ, который прямая должна составлять с осью ОХ.

Возможны и другие способы задания прямой.

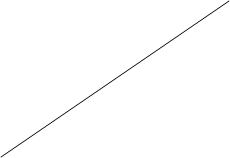
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Даны точка М0 (х0,у0) и вектор = {А, В} ≠ 0.

Составить уравнение прямой, проходящей через точку М0 и перпендикулярной вектору . Y

= {А, В}

.

М (х, у)

М0 (х0,у0)

О Х

М (х, у) в том и только том случае принадлежит прямой l, если ортогонален . Условие ортогональности 2-х векторов: (, ) = 0.

= {х-х0, у-у0}, ={А, В}.

А (х-х0) + В(у-у0) = 0 (1) – уравнение прямой, проходящей через точку М0 и перпендикулярной вектору .

называется вектором нормали, или нормальным вектором.

Для любой прямой существует бесконечно много нормальных векторов, все они коллинеарны друг другу.

Пример 1. Пусть заданы точка М0 (-1,2) и вектор = {5,-4}.

Написать уравнение прямой, проходящей через М0 перпендикулярно п.

5(х+1) – 4(у-2) = 0;

5х – 4у + 13 = 0.

Пример 2. На плоскости даны три точки: А(-1,2), В(3,5), С(4,-2).Составить уравнение высоты, проведенной из вершины А.

За вектор нормали примем вектор . А

= {4-3,-2-5}= {1,-7}.

1· (х + 1) – 7· (у-2) = 0; h

х – 7у + 15 = 0. С В

l

Общее уравнение прямой.

Уравнение (1) после раскрытия скобок приобретает вид

А (х-х0) + В (у-у0) = 0.

А х + Ву + (-Ах0-Ву0) = 0.

А х + Ву + С = 0 – общее уравнение прямой.

! Замечание. А и В – координаты вектора нормали.

Итак, если фиксирована декартова прямоугольная система координат. То в этой системе:

1) каждая прямая задаётся уравнением первой степени Ах + Ву + С = 0, где хотя бы один из коэффициентов А или В отличен от нуля;

2) каждое уравнение вида Ах + Ву + С = 0, где хотя бы один из коэффициентов А или В отличен от нуля, определяет прямую линию.

! Коэффициенты А и В в уравнении А х + Ву + С = 0 прямой являются координатами нормального вектора этой прямой.

Уравнение прямой, параллельной данной прямой.

Уравнение прямой, перпендикулярной данной прямой.

Рассмотрим общее уравнение прямой

А х + Ву + С = 0. (1)

= {А, В} – нормальный вектор прямой.

Справедливы следующие предложения:

1) если прямая l задана уравнением (1),то любая прямая l1 параллельная l может быть задана уравнением:

А х + Ву + С' = 0. (2)

2) если прямая l задана уравнением (1), то любая прямая l2 перпендикулярная l может быть задана уравнением:

В х – Ау + С" = 0. (3)

Докажем утверждение 1). При любом значении С' прямая (2) параллельна прямой (1), т.к. имеет тот же самый нормальный вектор. С другой стороны, какова бы ни была точка М0 (х0,у0), подбирая значение С', можно «заставить» прямую (2) пройти через эту точку (нужно взять точку С'= -Ах0-Ву0); следовательно, изменяя С', можно получить любую прямую, параллельную l.

Докажем утверждение 2).Т. к. l2 перпендикулярна l, то вектор нормали перпендикулярен 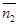, следовательно (, 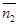) = 0 и АВ – ВА = 0. С другой стороны, какова бы ни была точка М0 (х0,у0), подбирая значение С", можно «заставить» прямую (3) пройти через эту точку; это значит, что, изменяя С", мы можем получить любую прямую, перпендикулярную l.

Пример. Прямая l задана уравнением 3х – 7у + 12 = 0.

Написать уравнения прямых, проходящих через точку (5,1) параллельно l и перпендикулярно l.

а) 3х – 7у + С' = 0,

3 · 5 – 7 · 1 = - С',

С'= -8.

3х – 7у – 8 = 0.

б) –7х – 3у + С" = 0,

-7 · 5 – 3 · 1 + С"= 0,

С"= 38.

-7х – 3у + 38 = 0.

Уравнение прямой, проходящей через данную точку параллельно заданному вектору.

Даны точка М0 (х0,у0) и вектор = {p, q}, отличный от нуля. Написать уравнение прямой l, проходящей через точку М0 и параллельной вектору

Y

М

М0

.

О Х

Рассмотрим случай, когда p,q ≠ 0 (если p = 0 или q = 0,то прямая l параллельна оси ОУ или ОХ, и её уравнение имеет вид х = х0 или у = у0).

Точка М (х, у) принадлежит прямой l тогда и только тогда, когда вектор коллинеарен вектору , что в свою очередь имеет место, когда координаты вектора пропорциональны координатам вектора , т.е.

- уравнение прямой, проходящей через точку М0 (х0,у0) параллельно вектору = {p,q}.

Вектор называется направляющим вектором прямой. Существует бесконечное множество направляющих векторов для каждой прямой, все они коллинеарны друг другу.

Легко написать уравнение прямой, проходящей через 2 точки: М0(х0,у0) и М1(х1,у1). За направляющий вектор примем вектор , его координаты:

р = х1 – х0, q = у1 – у0, следовательно

– уравнение прямой, проходящей через 2 точки.

Если х1 = х0, то прямая l параллельна оси ОУ, её уравнение: х = х0.

Если у1 = у0, то прямая l параллельна оси ОХ, её уравнение: у = у0.

Пример 1. Даны 3 точки: А(-1,7), В(0,9), С(1,3). Составить уравнение прямой, проходящей через точку А и параллельной прямой ВС.

= { 1-0, 3-9}={1,-6}, p = 1, q = -6, x0 = -1, y0 = 7.

или 6x + y – 1 = 0.

Пример 2. Дан треугольник с вершинами А(0,7), В(2,5), С(6,-4).Составить уравнение медианы, проведённой из вершины С.

Пусть Р – середина отрезка АВ. Координаты точки Р:

х0 = у0 =

Р(1,6). Т.к. медиана проходит через точки С и Р, её уравнение запишем как уравнение прямой, проходящей через 2 точки М0 (1,6) и М1(6,-4):

или 2х + у – 8 = 0.

Уравнение прямой в отрезках.

Пусть на координатных осях заданы две точки, отличные от начала координат: А (а, 0) на оси ОХ (а ≠ 0) и В (0,b) на оси ОY(b ≠ 0).

Рассмотрим уравнение: (*)

Этому уравнению удовлетворяют как координаты точки А, так и координаты точки В, следовательно, уравнение (*) определяет прямую АВ. У

Y

В

О А Х

Уравнение (*) называется уравнением прямой в отрезках.

Числа а и b указывают, какие отрезки отсекаются на осях ОХ и ОУ. К виду (*) можно привести любое уравнение

Ах + В у + С = 0,

если все три числа А,В,С ≠ 0.

Ах + В у = - С;

Например: 5х – 2у + 10 = 0,

Пример. Через точку Р(3,2) провести прямую так, чтобы её отрезок, заключённый между осями координат, делился в данной точке пополам.

Y

В(0,b)

•Р

О А(а,0) Х

Уравнение искомой прямой запишем в виде ;

Р – середина отрезка АВ, где А(а,0),В(0, b),

следовательно, , т.е. а = 6, b = 4.

Итак, уравнение искомой прямой имеет вид

Угловой коэффициент прямой.

Рассмотрим произвольную прямую l на плоскости.

Углом наклона прямой к оси ОХ назовём угол φ, на который нужно повернуть ось ОХ, чтобы она совместилась с l. Положительным считается направление против часовой стрелки. Введённый т.о. угол определён неоднозначно, за угол наклона принимают наименьший неотрицательный угол поворота, т.е. такой, что

Величину k = tg φ назовём угловым коэффициентом прямой l ().

!Замечание. Если φ = π /2, то tg φ не существует. Следовательно, прямая, параллельная оси ОУ, углового коэффициента не имеет. В остальных случаях угловой коэффициент существует.

Для нахождения углового коэффициента прямой достаточно знать 2 две её точки. Если М0(х0,у0) и М1(х1,у1) – две точки на прямой l, тогда

k = .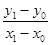

Доказательство.

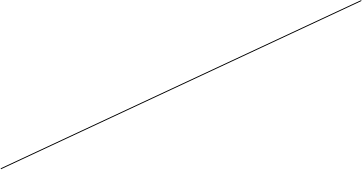
Y

·М1(х1,у1)

у1 – у0

О

М0(х0,у0)

х1 – х0

Пример 1. Прямая, проходящая через точки А(а,0) и В(0,b),имеет угловой коэффициент k =

Пример 2. Прямая, проходящая через начало координат (0,0) и А (а, b), имеет угловой коэффициент k =

Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом..

Даны точка М0 (х0,у0) на плоскости и число k. Составить уравнение прямой l, проходящей через точку М0 и имеющей угловой коэффициент k.

Если точка М (х, у) лежит на прямой l, то имеем:

Если же точка М не лежит на прямой l, то это равенство не выполняется. Значит, записанное равенство и является уравнением прямой. Перепишем это уравнение в виде

у – у0 = k ∙ (х – х0) –

уравнение прямой, проходящей через точку М0 и имеющей угловой коэффициент k.

В этом виде может быть записано уравнение любой прямой, не параллельной оси ОУ.

Если прямая, заданная общим уравнением Ах + ВУ + С = 0, не параллельна оси ОУ (т.е. В 0), то Ву = -Ах – С, т.е. у = -А/В ∙ х – С/В, следовательно,

k = -А/В.

Пример 1. Найти угловой коэффициент прямой

3х + 5у – 7 = 0.

5у = -3х + 7, у = -3/5х + 7/5, k = -3/5.

Пример 2. Составить уравнение прямой, проходящей через точку М0(2,1) и имеющей угловой коэффициент k = -1.

у – у0 = k ∙ (х – х0), у – 1 = -1∙ (х – 2), х + у – 3 = 0.

Угол между прямыми.

Рассмотрим на плоскости 2 прямые l 1 и l 2. Пусть k 1 и k 2 -их угловые коэффициенты. Угол φ, на который нужно повернуть первую прямую до совпадения со второй, называется углом наклона 2-ой прямой к первой.

Если поворот осуществляется против часовой стрелки, φ считают положительным, поворот по часовой стрелке считают отрицательным.

Y l2 l1

О Х

Если k 1и k 2 -углы наклона прямых l 1 и l 2 к оси ОХ, то угол φ между прямыми

φ = φ1 - φ2; tg φ = tg (φ1 - φ2) =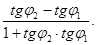

tg φ1 = k 1, tg φ2 = k2, следовательно,

tg φ =

Получена формула для нахождения угла между двумя прямыми, если известны угловые коэффициенты этих прямых.

Если знаменатель = 0, формула теряет смысл, следовательно в этом случае не существует tg φ, т.е. φ = π/2.Отсюда имеем условие перпендикулярности двух прямых:

k 1 k 2 + 1 = 0 или k 2 = - 1/ k 1.

Пример. Определить угол φ между прямыми 3х – 5у + 7 = 0 и

2х – 3у + 4 = 0.

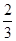k 1= , k 2 = , следовательно,

tg φ =

Взаимное расположение 2-х прямых на плоскости.

Пусть на плоскости заданы 2 прямые l 1 и l 2:

l 1: А1х + В1у + С1 = 0;

l 2: А2х + В2у + С2 = 0.

Покажем, что по заданным уравнениям прямых l 1 и l 2 можно судить об их взаимном расположении.

Возможны три случая.

1). Прямые l 1 и l 2 cовпадают, следовательно, вектор нормали к оллинеарен вектору нормали .

= {A1,B1}, = {A2,B2}.

≠ 0, следовательно, существует число λ такое, что

= λ· , т. е. А2 = λ · А1, В2 = λ · В1.

Перепишем уравнения прямых

А1х + В1у + С1 = 0 (уравнение l 1), (1)

λ·А1х +λ·В1у + С1 = 0 (уравнение l 2). (2)

Любая точка прямой l 1 (или l 2) удовлетворяет обоим написанным уравнениям, а значит, и уравнению:

0·х + 0·у + (С2 - λ·С1) = 0, (3)

которое получится, если из обеих частей второго уравнения вычесть соответственные части первого уравнения. Но уравнение вида (3) имеет решение лишь в том случае, когда его свободный член равен 0, т.е. С2 =λ·С1.

Итак, условием совпадения прямых l1 и l2 является существование такого числа λ, что А2 = λ · А1, В2 = λ · В1, С2 =λ·С1.

Смысл этого условия состоит в том, что одно из уравнений (1) или (2) получается из другого умножением обеих частей на одно и то же число λ.

2). Прямые l 1 и l 2 не совпадают и параллельны. Как и в первом случае, отсюда следует, что вектор нормали коллинеарен вектору нормали ,

т.е. А2 = λ · А1, В2 = λ ∙ В1, но С2 ≠ λ ·С 1, иначе l 1и l 2 совпадут.

Итак, условием того, что прямые l1 и l2 параллельны, но не совпадают, является существование такого числа λ, что

А2 = λ · А1, В2 = λ ∙ В1, но С2 ≠ λ ·С 1.

Пример. Прямые и 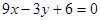совпадают, т.к.

Прямые и параллельны, т.к.

3). Прямые l 1 и l 2 не параллельны, т.е. пересекаются в единственной точке. В этом случае их нормальные векторы и неколлинеарны. И обратно, если нормальные векторы и неколлинеарны, то сами прямые l 1 и l 2 не параллельны.

Итак, условием непараллельности прямых l1 и l2 является неколлинеарность их нормальных векторов и .

Учитывая, что векторы {A1,B1}и {A2,B2}не коллинеарны тогда и только тогда, когда определитель, составленный из их координат не равен 0, можно сделать вывод, что условием непараллельности прямых l1 и l2 является

Если прямые l 1 и l 2 не параллельны, их точку пересечения можно найти, решая систему из уравнений (1) и (2).

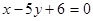Пример. Проверить, что прямые и не параллельны, и найти их точку пересечения.

Прямые не параллельны, т.к.

Точку пересечения прямых находим, решая систему

Точка пересечения – (-1;1).

Параметрические уравнения прямой.

Пусть прямая проходит через точку М0 и параллельна вектору Тогда условием принадлежности точки М данной прямой является коллинеарность векторов и Иначе говоря, точка М лежит на данной прямой в том и только в том случае, когда для некоторого числа t выполняется равенство

= t (1)

Y

М

М0

О Х

Введём на плоскости прямоугольную декартову систему координат. Пусть в этой системе даны точка М0 (х0,у0) и вектор . Координаты текущей точки М обозначим через x и y.

. Тогда векторное равенство (1) примет вид или

(2)

Если параметр t принимает все значения от до + 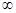, точка М с координатами x и y, определёнными с помощью формул (2), пробегает всю прямую.

Итак, формулы (2) дают параметрические уравнения прямой, проходящей через точку М0 (х0,у0) и параллельной вектору .

Пример. Параметрические уравнения прямой, проходящей через точку

М0 (2,-1) и параллельной вектору , имеют вид

Расстояние от точки до прямой на плоскости.

На плоскости даны точка М0(х0, у0) и прямая l, определяемая уравнением Ах + Ву + С = 0.

Требуется вычислить расстояние d от точки М0 до прямой l.

l

М0

d

О Х

.

Чтобы найти расстояние от точки М0 до прямой l, заданной общим уравнением, нужно в левую часть этого уравнения вместо текущих координат x и y подставить координаты точки М0 и взять абсолютную величину этого выражения, разделённую на .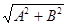

Пример1. Прямая задана уравнением 3х - 4у +10 = 0.Найти расстояние от точки М (4,3) до этой прямой.

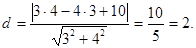
Пример 2. Найти расстояние между параллельными прямыми

3х – 4у + 10 = 0 и 3х – 4у –5 =0.

На второй прямой берём любую точку, например (3,1), и находим расстояние от неё до первой прямой:

Полуплоскости, определяемые прямой.

Пусть на плоскости в прямоугольных декартовых координатах задана прямая линия

Ах + Ву + С = 0. (1)

По отношению к прямой вся плоскость распадается на две полуплоскости, для которых эта прямая является общей границей.

Докажем следующее утверждение: одна из полуплоскостей, определяемых прямой (1), состоит из точек (x, y), для которых

Ах + Ву + С 0,

а другая - из точек (x, y), для которых

Ах + Ву + С 0

Date: 2015-12-10; view: 606; Нарушение авторских прав