Группа. Кольцо. Поле

Пусть дано множество A, где определена алгебраическая операция 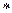, т.е. пара - алгебра.

Пара называется группой, если операция 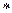обладает свойствами (аксиомы группы):

1) алгебраическая операция 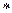ассоциативна ,

2) относительно 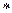существует нейтральный элемент:

,

3) Для всякого элемента существует симметричный элемент:

,

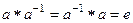Проверим, что векторное пространство относительно сложения векторов есть группа: .

В самом деле, множество замкнуто относительно сложения векторов, т.е. на определена алгебраическая операция сложения векторов: и .

1) сложение векторов ассоциативно, т.е. для всякой тройки векторов имеет место: ,

2) нейтральным элементом является нуль вектор 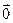, т.е.

,

3) для всякого вектора 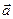симметричным относительно сложения векторов является противоположный вектор - 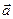, т.е.

.

Таким образом, – группа.

Группа относительно сложения «+» называется аддитивной, а группа относительно умножения «◦» называется мультипликативной. Значит, - аддитивная группа, можно убедиться, что - мультипликативная группа.

Группа называется коммутативной или абелевой, если операция 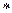коммутативна на A.

Пусть на множестве A определены две операции 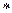и ◦, т.е. определена упорядоченная тройка .

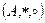Тройка 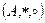называется кольцом, если:

1) - коммутативная группа,

2) операция ◦ ассоциативна и дистрибутивна относительно 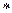, т.е. для всяких a,b,c из A

,

.

Например, множество Z целых чисел образует кольцо т.к. - аддитивная абелева группа, а операция умножения на Z ассоциативна и дистрибутивна относительно сложения.

Кольцо 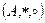, которое относительно алгебраической операции ◦ образует некоммутативную группу, называется телом.

Тело , коммутативное относительно операции •, называется полем.

Например ; – примеры полей, – не является полем.

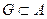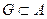Пусть группа, то подмножество называется подгруппой группы , если - группа. Имеет место: - подгруппа группы тогда и только тогда, когда выполнены условия:

Ι) и ;

ΙΙ) , где .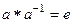

Для доказательства утверждения достаточно проверить выполнимость условий определения (аксиом) группы:

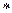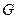1) операция в ассоциативна в силу Ι, т.к. она ассоциативна в ,

2) в силу ΙΙ и Ι в G существует нейтральный элемент ,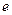

3) существование симметричного элемента для всякого элемента определяется предложением ΙΙ.

Date: 2015-12-10; view: 387; Нарушение авторских прав