
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Сферическая система координат
| Рисунок 6.2 |
 В сферической системе координат положение точки в пространстве характеризуется тоже тремя координатами:
В сферической системе координат положение точки в пространстве характеризуется тоже тремя координатами:  - расстояние от начала координат до самой точки
- расстояние от начала координат до самой точки 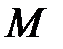 ,
,  -угол поворота радиус-вектора проекции
-угол поворота радиус-вектора проекции  точки
точки  на плоскость
на плоскость 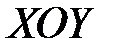 относительно оси
относительно оси 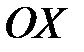 ,
, 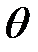 -угол между радиус-вектором точки
-угол между радиус-вектором точки  и
и | Рисунок 6. 3 |
 (см. рис. 6.2).
(см. рис. 6.2).
Связь между сферическими и декартовыми координатами выглядит следующим образом:  , (6.4) где
, (6.4) где  .
.
Заметим, что при этом  . Самостоятельно вычислите Якобиан и убедитесь в том, что при переходе к сферической системе
. Самостоятельно вычислите Якобиан и убедитесь в том, что при переходе к сферической системе  . Следовательно, переходя к сферическим координатам, имеем:
. Следовательно, переходя к сферическим координатам, имеем:
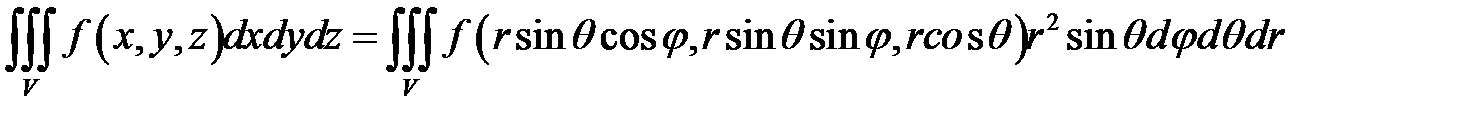 (6.5)
(6.5)
Замечание 2. В сферических координатах уравнение сферы 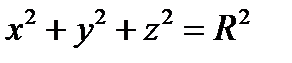 принимает вид
принимает вид 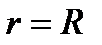 , уравнение кругового конуса
, уравнение кругового конуса  принимает вид
принимает вид  . Поэтому целесообразно переходить к этим координатам, если в условии задачи присутствуют конусы и сферы. Замечание 3. Чтобы преобразовать тройной интеграл в сферической системе координат в повторный, можно поступить следующим образом. Пересечём тело, занимающее область
. Поэтому целесообразно переходить к этим координатам, если в условии задачи присутствуют конусы и сферы. Замечание 3. Чтобы преобразовать тройной интеграл в сферической системе координат в повторный, можно поступить следующим образом. Пересечём тело, занимающее область 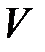 , полуплоскостью, проходящей через ось
, полуплоскостью, проходящей через ось  , и выделим площадку
, и выделим площадку  , которая при этом получится. Через ось
, которая при этом получится. Через ось  построим две полуплоскости, которые образуют двухгранный угол, внутри которого заключено тело. Для этого двухгранного угла, а значит, и для области
построим две полуплоскости, которые образуют двухгранный угол, внутри которого заключено тело. Для этого двухгранного угла, а значит, и для области 
 . И тогда
. И тогда 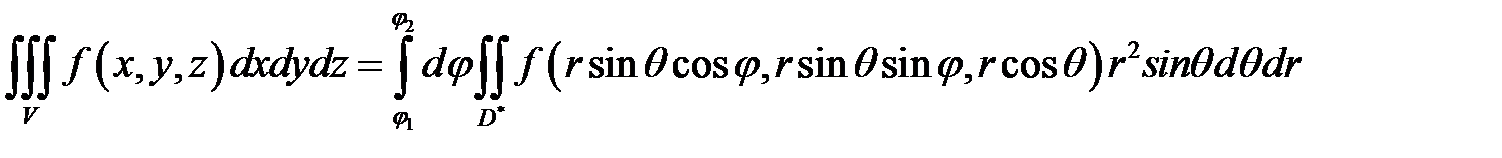 (6.5а) В двойном интеграле по области
(6.5а) В двойном интеграле по области  пределы расставим как в полярной системе координат с той разницей, что переменная
пределы расставим как в полярной системе координат с той разницей, что переменная  меняется от вертикальной оси, где она равна нулю, возрастая против часовой стрелки.
меняется от вертикальной оси, где она равна нулю, возрастая против часовой стрелки.
Пример 6.1. Вычислим объём тела, заключённого между двумя полусферами  и
и  и двумя коническими поверхностями
и двумя коническими поверхностями  и
и  .
.
 Решение. Согласно вышесказанному, уравнения сфер в сферических координатах примут вид
Решение. Согласно вышесказанному, уравнения сфер в сферических координатах примут вид 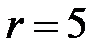 и
и  . Уравнения конусов, являющихся телесными углами, примут вид
. Уравнения конусов, являющихся телесными углами, примут вид  и
и  соответственно, в чём легко убедиться,заменив в уравнениях поверхностей декартовы переменные сферическими (см. (6.4)).
соответственно, в чём легко убедиться,заменив в уравнениях поверхностей декартовы переменные сферическими (см. (6.4)).
| Рисунок 6.3 |
 Чтобы преобразовать тройной интеграл в сферической системе координат в повторный (см. замечание 3), пересечём тело, занимающее область
Чтобы преобразовать тройной интеграл в сферической системе координат в повторный (см. замечание 3), пересечём тело, занимающее область 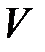 , полуплоскостью, проходящей через ось
, полуплоскостью, проходящей через ось  , и выделим площадку
, и выделим площадку  , которая при этом получится (на рис. 6.3 эта площадка справа выделена синим). Для того, чтобы получить всё тело, площадку
, которая при этом получится (на рис. 6.3 эта площадка справа выделена синим). Для того, чтобы получить всё тело, площадку 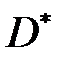 надо провращать вокруг оси
надо провращать вокруг оси  на угол
на угол 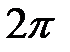 . Тогда
. Тогда 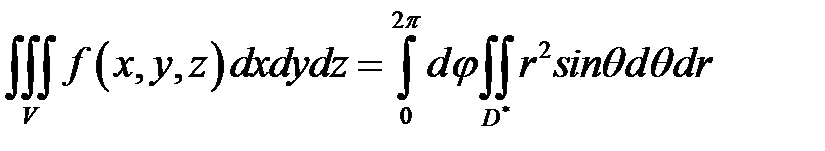 В двойном интеграле по области
В двойном интеграле по области  пределы расставим как в полярной системе координат с той разницей, что переменная
пределы расставим как в полярной системе координат с той разницей, что переменная  меняется от вертикальной оси, где она равна нулю, возрастая против часовой стрелки. Т.е.
меняется от вертикальной оси, где она равна нулю, возрастая против часовой стрелки. Т.е.  . И окончательно, получаем
. И окончательно, получаем 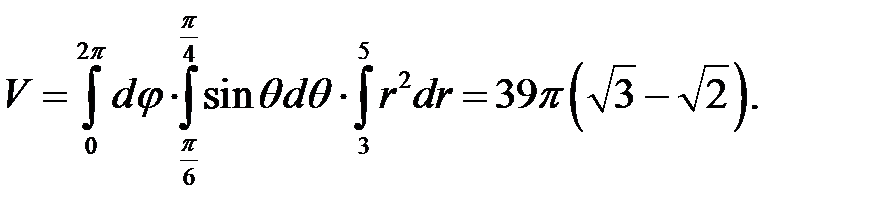
Пример 6.2. Найдём объём тела, заданного системой неравенств  , с помощью тройного интеграла.
, с помощью тройного интеграла.
Решение. Построим сферу и параболоид, заданные в условии, и выделим тело, ограниченное ими.
| Рисунок 6.4 |
| Рисунок 6.4 |
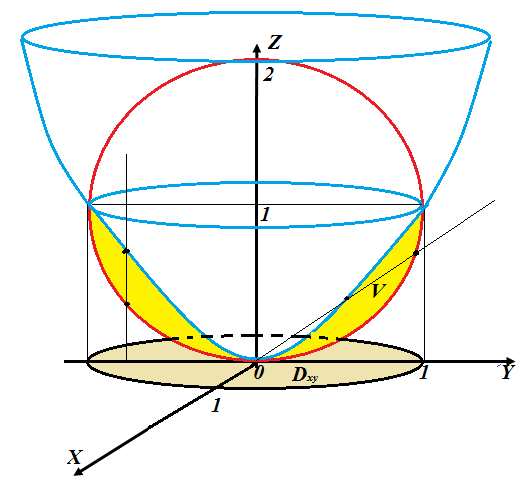 Замечание. Уравнения обеих поверхностей имеют вид
Замечание. Уравнения обеих поверхностей имеют вид 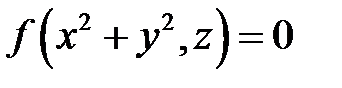 , что говорит о том, что это поверхности вращения вокруг оси
, что говорит о том, что это поверхности вращения вокруг оси  . Поэтому тело вращения, ограниченное ими, можно построить следующим образом. Строим линии пересечения поверхностей с полуплоскостью
. Поэтому тело вращения, ограниченное ими, можно построить следующим образом. Строим линии пересечения поверхностей с полуплоскостью  , выделяем область
, выделяем область 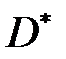 , ограниченную этими линиями (на рис. 6.4 эта область справа выделена жёлтым цветом), и вращаем
, ограниченную этими линиями (на рис. 6.4 эта область справа выделена жёлтым цветом), и вращаем 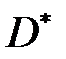 вокруг оси
вокруг оси  . Получаем заданное в условии задачи тело, которое в пространстве занимает область
. Получаем заданное в условии задачи тело, которое в пространстве занимает область 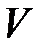 (см. рис. 6.4). 1 способ. Рассмотрим решение задачи в цилиндрической системе координат. Заданное тело заключено внутри цилиндра с образующей, параллельной оси
(см. рис. 6.4). 1 способ. Рассмотрим решение задачи в цилиндрической системе координат. Заданное тело заключено внутри цилиндра с образующей, параллельной оси  , проходящей через линию пересечения сферы и параболоида. Чтобы составить его уравнение, которое совпадёт с уравнением границы области
, проходящей через линию пересечения сферы и параболоида. Чтобы составить его уравнение, которое совпадёт с уравнением границы области  (см. рис. 6.4), необходимо из системы уравнений этих поверхностей исключить переменную
(см. рис. 6.4), необходимо из системы уравнений этих поверхностей исключить переменную  .
. 
 . Область
. Область  , на которую проектируется тело, представляет собой круг
, на которую проектируется тело, представляет собой круг  . Область
. Область 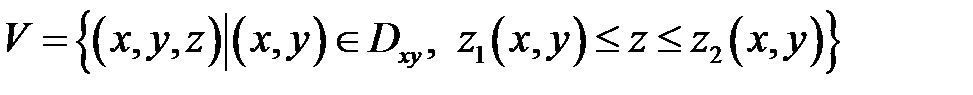 является правильной. Перейдём к цилиндрической системе координат. После замены переменных (см. (6.2)) получим: уравнение границы области
является правильной. Перейдём к цилиндрической системе координат. После замены переменных (см. (6.2)) получим: уравнение границы области  -
-  ,
,
уравнение нижней части сферы-  ,
,
уравнение параболоида- z=r2. Обратите внимание на прямую линию в левой части рисунка 6.4. Мы видим, что при возрастании переменной  сферическая поверхность ограничивает тело снизу, а параболическая – сверху. Объём тела вычислим как тройной интеграл, где
сферическая поверхность ограничивает тело снизу, а параболическая – сверху. Объём тела вычислим как тройной интеграл, где 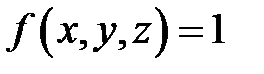 (см. свойства).
(см. свойства).  (см. (6.3а)). Область
(см. (6.3а)). Область  является радиально правильной. Расставим пределы в повторном интеграле и вычислим его.
является радиально правильной. Расставим пределы в повторном интеграле и вычислим его.

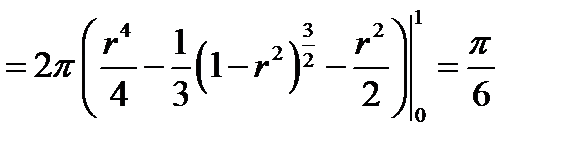 .
.
2 способ. Рассмотрим решение этой же задачи в сферической системе координат.  . Преобразуем уравнения поверхностей. Уравнение сферы примет вид:
. Преобразуем уравнения поверхностей. Уравнение сферы примет вид: 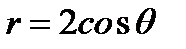 .
.
Уравнение параболоида:  . Чтобы расставить пределы интегрирования в повторном интеграле, пересечём область
. Чтобы расставить пределы интегрирования в повторном интеграле, пересечём область  полуплоскостью, проходящей через ось
полуплоскостью, проходящей через ось 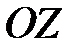 . Получим плоскую область
. Получим плоскую область  (на рис. 6.3 она справа закрашена жёлтым цветом). Так как область
(на рис. 6.3 она справа закрашена жёлтым цветом). Так как область  была получена при вращении этой площадки
была получена при вращении этой площадки  вокруг оси
вокруг оси  , для всех точек
, для всех точек 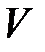 переменная
переменная  . И тогда
. И тогда 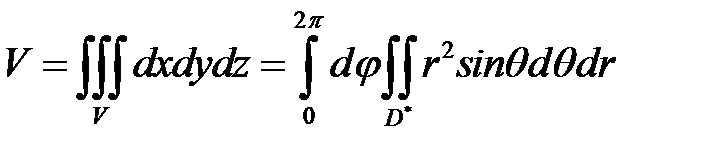 . (см. (6.5а)) Область
. (см. (6.5а)) Область  является радиально правильной и для всех её точек
является радиально правильной и для всех её точек  , а переменная
, а переменная 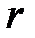 меняется от
меняется от 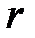 параболоида до
параболоида до 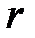 сферы. (Обратите внимание на прямую линию в правой части рисунка 6.3)
сферы. (Обратите внимание на прямую линию в правой части рисунка 6.3)
В соответствии с данными рассуждениями составим повторный тройной интеграл в сферической системе координат и вычислим его:

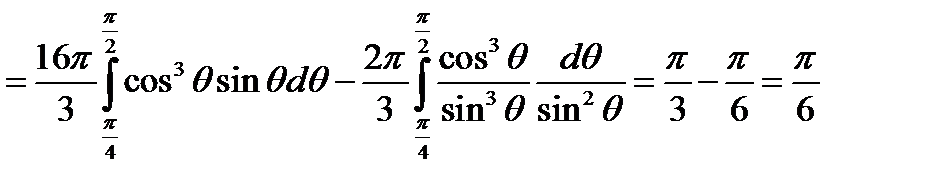 .
.
Пример 6.3. Найдём объёма тела, ограниченного поверхностями 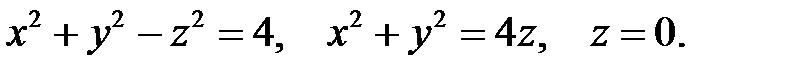
Решение. Построим тело, ограниченное данными поверхностями, учитывая то, что оно является телом вращения, поскольку уравнения всех поверхностей зависят от  . Для этого пересечём поверхности
. Для этого пересечём поверхности

| Рисунок 6.5 |
| Рисунок 6.7 |
 полуплоскостью
полуплоскостью 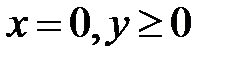 и выделим область
и выделим область  , ограниченную полученными линиями, а менно, гиперболой
, ограниченную полученными линиями, а менно, гиперболой 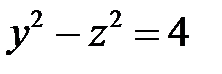 и параболой
и параболой 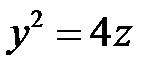 . (см. рис. 6.5) Найдём точку пересечения этих кривых. Она имеет координаты
. (см. рис. 6.5) Найдём точку пересечения этих кривых. Она имеет координаты 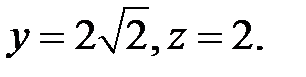
При вращении этой области вокруг оси  получим пространственную область
получим пространственную область  , которую занимает заданное тело. Эта область не является правильной, так как снизу ограничена двумя поверхностями, параболоидом и плоскостью
, которую занимает заданное тело. Эта область не является правильной, так как снизу ограничена двумя поверхностями, параболоидом и плоскостью  . Поэтому для вычисления требуемого объёма придётся разбить область на две правильные и тогда
. Поэтому для вычисления требуемого объёма придётся разбить область на две правильные и тогда 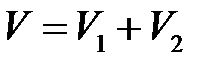 (см. рис. 6.6). В этом случае
(см. рис. 6.6). В этом случае

Область  на рис. 6.6 выделена тёмным сиреневым цветом.
на рис. 6.6 выделена тёмным сиреневым цветом.
| Рисунок 6.6 |
 . Область
. Область 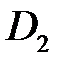 выделена светлым сиреневым цветом.Перейдём в цилиндрическую систему координат (см. (6.2)) и составим оба интеграла. Из формулы
выделена светлым сиреневым цветом.Перейдём в цилиндрическую систему координат (см. (6.2)) и составим оба интеграла. Из формулы  следует:
следует:  2-ой способ. Искомый объём можно найти иначе, а именно как
2-ой способ. Искомый объём можно найти иначе, а именно как  . (См. рис. (6.6)) Здесь
. (См. рис. (6.6)) Здесь 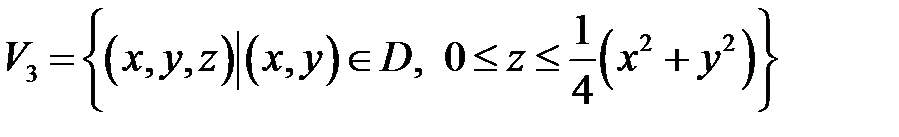 , причём область
, причём область  - круг
- круг  , а
, а 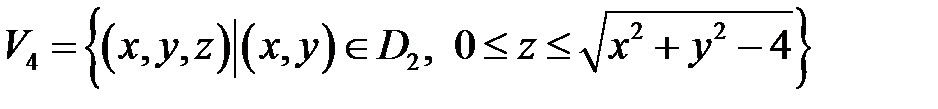 . И в этом случае
. И в этом случае 
3-ий способ. Наконец, можно изменить порядок интегрирования и составить повторный интеграл следующим образом:
 (В этом случае вращаем область
(В этом случае вращаем область  вокруг оси
вокруг оси  так, что
так, что  , а интеграл
, а интеграл 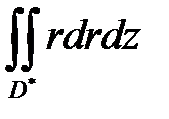 представляем как повторный по
представляем как повторный по  -правильной области
-правильной области  (см. рис.6.6, жёлтая область справа).
(см. рис.6.6, жёлтая область справа).
Домашнее задание к занятию 6:
ОЛ-6 №№ 2255, 2257, 2259, 2261, 2263 или ОЛ-5 №№ 8.123, 125, 126, 128.
Date: 2015-10-19; view: 4025; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |