Построение проекций многогранников и точек, расположенных на их поверхности

ИНЖЕНЕРНАЯ ГРАФИКА

Методические указания по выполнению графической работы

«Многогранники» для студентов 1 курса специальностей и направлений:

240500 - Эксплуатация судовых энергетических установок,

240600- Эксплуатация электрооборудования и

автоматики судов, 100100 - Электрические станции,

100500 - Тепловые электрические станции

Калининград

издательство КГТУ

УДК 744 629.12

УТВЕРЖДЕНО

Ректором Калининградского

государственного технического

университета

АВТОРЫ - Рудаченко С.В., канд. техи. наук, доцент кафедры инженерной графики Калининградского государственного технического университета

Рудаченко Т.В., канд. техн. наук, доцент той же кафедры

Методические указания рассмотрены и одобрены кафедрой инженерной графики Калининградского государственного технического университета 30 мая 2003 г., протокол №9.

РЕЦЕНЗЕНТ - кафедра инженерной графики Калининградского государственного технического университета

© Калининградского государственного технического университета 2003 г.

ОГЛАВЛЕНИЕ

1. Цель и содержание работы «Многогранники».……………………. 4

2. Построение проекций многогранников и точек,

расположенных на их поверхности..…………………………………….. 4

З. Построение проекций тел со сквозными отверстиями ……….10

4. Виды. Разрезы. Сечения ……………………………………………….14

5. Построение сечения тела проецирующей плоскостью ………. 17

6. Построение аксонометрии многогранника ……………………... 23

Приложение ………………………………………………………………… 28

Литература ………………………………………………………………..30

1. ЦЕЛЬ И СОДЕРЖАНИЕ РАБОТЫ «МНОГОГРАННИКИ»

Цель задания освоение правил построения изображений пространственных геометрических фигур способом ортогонального проецирования и требований ГОСТ 2.305-68 Единой системы конструкторской документации, а также проработка ГОСТ ЕСКД на форматы, линии чертежа, нанесение размеров.

Содержание работы:

1) Изучить ГОСТ 2.305-68 «Виды, разрезы, сечения».

2) По заданному главному виду многогранника достроить вид сверху и построить вид слева. (Многогранник состоит из правильной призмы и правильной пирамиды).

3) Построить линию пересечения многогранника с фронтально - проецирующим сквозным призматическим отверстием.

4) На виде слева выполнить разрез.

5) Построить натуральную величину наклонного сечения многогранника.

6) Выполнить аксонометрию многогранника с вырезом условной четверти.

7) Оформить работу (образец работы - рис. 1).

ПОСТРОЕНИЕ ПРОЕКЦИЙ МНОГОГРАННИКОВ И ТОЧЕК, РАСПОЛОЖЕННЫХ НА ИХ ПОВЕРХНОСТИ

Выполнение работы начинается с ознакомления с вариантом своего задания. Необходимо по главному виду и виду сверху определить, какие геометрические тела образуют многогранник.

Чтение заданных двух проекций начинают с чтения линий контура. Какие признаки позволяют установить, что на данном чертеже изображена именно призма? Наличие на чертеже только прямолинейных

5

отрезков, причем они служат проекциями или ребер, или граней, наличие прямоугольников как проекций боковых граней и любого многоугольника как проекции основания. Пирамида задается на чертеже проекциями ее основания и вершины, а усеченная пирамида - проекциями обоих оснований [1].

Для правильной шестиугольной призмы, чертеж которой в трех проекциях дан на рис. 2а, горизонтальная проекция представляет собой шестиугольник, каждая из сторон которого является проекцией боковой грани, а вершины - проекциями боковых ребер призмы. Фронтальная проекция представляет собой прямоугольник, у которого верхние и нижние стороны есть проекции оснований, а боковые стороны - проекции боковых ребер призмы [2].

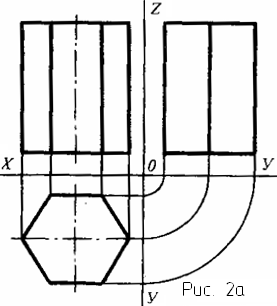
На рис. 2а показано также построение профильной проекции призмы по заданным ее фронтальной и горизонтальной проекциям. Для построения выбирают оси проекций Х, У и Z; и по правилам, известным из курса начертательной геометрии, строят профильную проекцию. Построение ясно из чертежа.

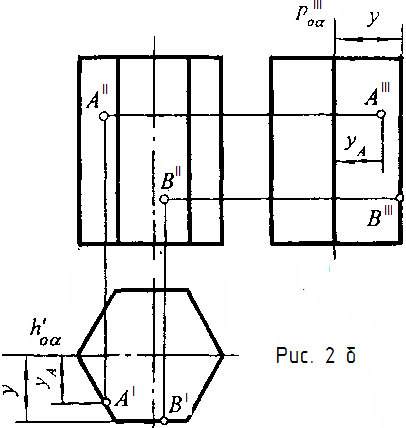
Можно выполнять чертежи без указания осей проекций. В этом случае (рис. 2б) какую-либо плоскость, параллельную плоскости π₂, принимают в качестве новой Координатной плоскости, от которой ведут отсчет координат у. Такой плоскостью в задаче рис. 2б выбрана плоскость симметрии призмы a. Ее горизонтальный след h^I_0a совпадает с осью симметрии горизонтальной проекции, профильный след р^III_0a проведен произвольно справа от фронтальной проекции и является

осью симметрии профильной проекции. Для построения, например, профильной проекции передней грани призмы измеряют отрезок, выражающий координату у этой грани, на горизонтальной проекции, и откладывают его на профильной проекции.

Для несимметричных фигур за координатную плоскость можно принять какую-либо ее грань или какую-либо плоскость, параллельную плоскости π₂

Машиностроительные чертежи выполняют без указания осей проекций. Этим способом построения следует пользоваться при выполнении данного задания.

Для нахождения проекций точки, принадлежащей поверхности тела, надо сначала определить вид поверхности, границы, найти проекции этой поверхности, а затем уже находить проекции заданной точки [2].

Например, на передней левой грани призмы рис.2б расположена точка А, на передней средней грани - точка В (заданы проекциями А^II и В^II). Требуется найти их горизонтальные и профильные проекции. Так как каждая из граней призмы является частью проецирующей плоскости, то для нахождения указанных проекций используют проецирующие свойства граней. для точки А необходимо сначала найти ее горизонтальную проекцию А^I и, воспользовавшись координатой y_А построить профильную проекцию А^III. для точки В горизонтальную и профильную проекции можно находить независимо друг от друга, что и показано на рис.2б.

На рис. 3 дан чертеж прямой правильной шестиугольной пирамиды. Ее основание параллельно плоскости π₁. Контур горизонтальной проекции пирамиды образован сторонами правильного шестиугольника, представляющего собой горизонтальную проекцию основания пирамиды. Центр шестиугольника есть горизонтальная проекция вершины

пирамиды; линии, соединяющие центр с вершинами, - проекции боковых ребер. Боковые грани пирамиды представляют собой треугольники. Их горизонтальные проекции - также треугольники. Контур фронтальной и профильной проекций образован сторонами равнобедренных треугольников, основания которых - соответствующие проекции основания пирамиды. Однако, если для фронтальной проекции боковые стороны треугольника для профильной - проекциями средних передней и задней граней.

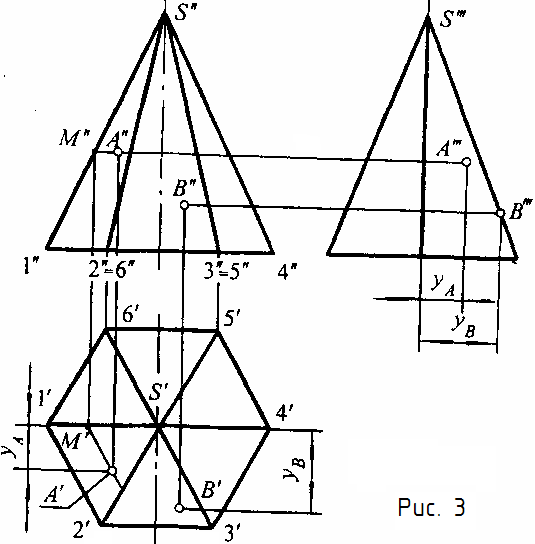
На передней левой грани пирамиды S12 расположена точка А, на передней средней грани S23 - точка В (заданы проекциями А^II и В^II). Требуется найти их горизонтальные и профильные проекции. Левая передняя грань - часть плоскости общего положения; для нахождения горизонтальной проекции точки А используем горизонталь плоскости (можно какую-либо иную прямую). Проводим ее фронтальную проекцию через А^II до пересечения с S^II1^II в точке М^II. Проекция горизонтали на плоскости π₁ проходит через точку М^I параллельно отрезку 1^I2^I. По А^II находим А^I на прямой А^IМ^I, а по А^II и А^I строим А^III, используя координату у_А. Передняя средняя грань S23 - часть профильно - проецирующей плоскости, поэтому для точки В сначала находим В^II, а затем с помощью координаты у_B строим В^I.

3. ПОСТРОЕНИЕ ПРОЕКЦИЙ ТЕЛ СО СКВОЗНЫМИ