
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Модифицированный симплексный метод решения задач целевого программирования
Рассмотрим метод решения задачи ЦП, использующий идеи симплексного метода. Основная особенность задач ЦП заключается в конструкции целевой функции и в переменных, которые показывают отклонения от желаемого уровня достижения целей. Если учесть эти особенности, то для решения таких задач может быть применён обычный симплексный метод. Проиллюстрируем это на рассмотренном ранее примере. Алгоритм в некоторой степени упрощается из-за того, что исходное базисное решение здесь очевидно. Роль базисных переменных для начального плана здесь играют отрицательные отклонения «d  », которые включены в модель с коэффициентами +1. Сложнее со строкой для коэффициентов целевой функции, т.е. с оценочной строкой. Как мы знаем, коэффициентами для отклонений в целевой функции задачи ЦП служат веса, ранжирующие цели по приоритетам. Их численные значения, как правило, не определены. Важно, чтобы коэффициент при отклонении для целевого ограничения с более высоким приоритетом был бы значимо больше коэффициента при отклонении от цели с более низким приоритетом. Поэтому для удобства расчетов оценочная строка разбивается на несколько строк (по числу приоритетов), и вычисления ведутся по каждой строке в отдельности.
», которые включены в модель с коэффициентами +1. Сложнее со строкой для коэффициентов целевой функции, т.е. с оценочной строкой. Как мы знаем, коэффициентами для отклонений в целевой функции задачи ЦП служат веса, ранжирующие цели по приоритетам. Их численные значения, как правило, не определены. Важно, чтобы коэффициент при отклонении для целевого ограничения с более высоким приоритетом был бы значимо больше коэффициента при отклонении от цели с более низким приоритетом. Поэтому для удобства расчетов оценочная строка разбивается на несколько строк (по числу приоритетов), и вычисления ведутся по каждой строке в отдельности.
Итак, пусть решается задача min Z = P1d1- + P2d2- + P3d3+ + P4d4 -,
при условии, что
7x1 + 6x2 + d1- – d1+ = 30;
2x1 + 3x2 + d2- – d2+ = 12;
6x1 + 5x2 + d3- – d3+ = 30;
x2 + d4 - – d4+ = 7;
x1, x2, di-, di+ ³ 0 (i = 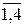 ).
).
Составим исходную симплексную таблицу (таблица 5.1.)
Таблица 5.1 – Исходная симплексная таблица
| Cj CB | Базис | Реше-ние | 0 x1 | 0 x2 | P1 d1- | P2 d2- | d3- | P4 d4- | d1+ | d2+ | P3 d3+ | d4+ | q |
| P1 P2 P4 | d1- d2- d3- d4- |  7 7
| -1 | -1 | -1 | -1 | 30/7 30/6 - | ||||||
| Zj– Сj | P4 P3 P2 P1 | -1 | -1 | -1 | -1 |
Как известно, элементы оценочной строки (Zj – Cj) рассчитываются по правилу: «от суммы произведений элементов столбца «Св» на элементы соответствующего столбца отнимается элемент верхней строки». Например, для столбца «решение» элемент «Zj – Cj» равен: Р1 *30 + Р2 *12 + 0* 30 + р4 *7 – 0 = 30Р1 + 12Р2 + 7Р4 и коэффициенты при соответствующих Pi (i = 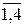 ) выписаны в этом столбце в блоке «Zj – Cj» (читать снизу вверх). Для столбца «х1»: Р1 *7 + Р2 *2 + 0 * 6 + Р4 *0 – 0 = 7Р1 + 2Р2, а это и есть коэффициенты при Р1 и Р2 в блоке «Zj – Cj» и т.д.
) выписаны в этом столбце в блоке «Zj – Cj» (читать снизу вверх). Для столбца «х1»: Р1 *7 + Р2 *2 + 0 * 6 + Р4 *0 – 0 = 7Р1 + 2Р2, а это и есть коэффициенты при Р1 и Р2 в блоке «Zj – Cj» и т.д.
Поскольку задача ЦП всегда решается на минимум, то решение будет оптимальным, если все элементы оценочной строки будут не положительны. В нашем случае две оценки (в столбцах «х1» и «х2») положительны, следовательно, план не оптимальный. Для определения переменной, входящей в базис, на первой итерации определяем наибольшую положительную оценку. Определяется она по знаку коэффициента при Р1, т.к. P1 >> P2 >> P3 >> P4. При равных коэффициентах при Р1, «поднимаемся» на строку выше и выбираем наибольший коэффициент там. В случае полного равенства по всем строкам – выбирается любой из них. В нашем случае разрешающим столбцом будет столбец «х1» (т.к. 7 > 6). Разрешающая строка выбирается так же как и в симплексном методе – по наименьшему симплексному отношению q (элементы столбца «решение» делим на положительные элементы разрешающего столбца). В таблице 5.1 наименьшее отношение q находится в первой строке. Итак, на следующей итерации в базис вводится переменная «х1», выводится «d1-». Пересчитываем таблицу как в обычном симплекс-методе (таблица 5.2.)
Таблица 5.2 – Вторая симплексная таблица
| Cj CB | Базис | Решение | x1 | x2 | P1 d1- | P2 d2- | d3- | P4 d4- | d1+ | d2+ | P3 d3+ | d4+ | q |
| P2 P4 | x1 d2- d3- d4- | 30/7 24/7 30/7 | 6/7 9/7 1/7 | 1/7 2/7 6/7 | 1/7 2/7 6/7 | -1 | -1 | -1 | 30/6 24/9 - | ||||
| Zj – Cj | P4 P3 P2 P1 | 24/7 | 9/7 | 2/7 -1 | 2/7 | -1 | -1 | -1 |
Как видим, на второй итерации из базиса выводится d2-, в базис вводится х2. И т.д., пока не получим оптимальное решение. После 4-й итерации получим таблицу 5.3.
Таблица 5.3 – Итоговая симплексная таблица
| Cj CB | Базис | Реше-ние | x1 | x2 | P1 d1- | P2 d2- | d3- | P4 d4- | d1+ | d2+ | P3 d3+ | d4+ |
| P4 | d2+ x2 d1+ d4- | 1,6 1,2 0,2 -1,2 | -1 | -1 | 0,6 0,2 1,2 -0,2 | -0,6 -0,2 -1,2 0,2 | -1 | |||||
| Zj – Cj | P4 P3 P2 P1 | -1,2 | -1 | -1 | -0,2 | 0,2 -1 | -1 |
Тот факт, что в строке при P4 имеется положительный элемент (в столбце d3+) означает, что четвёртая цель выполнена не полностью. При этом, целевая функция равна Р4, это минимально возможное её значение. В целом оценка переменной d3+ равна (0,2 Р4 – Р3), и поскольку Р3 >> Р4, то в итоге она отрицательна. Все остальные оценки неположительны, следовательно, план с точки зрения симплексного метода оптимален.
Решение этой задачи можно прокомментировать следующим образом. Для выполнения поставленной задачи необходимо выпустить вторую продукцию в объёме 6 ед. (х2 = 6). Первую продукцию не выпускать. При этом первая и вторая цели перевыполнены на 6 ед. (d1+ = d2+ = 6), а четвёртая недовыполнена на 1ед. (d4- =1). Таким образом, прибыли получили на 6 ед. больше желаемого уровня, первый ресурс использован сверх нормального лимита на 6 ед., а продукцию 2-го вида выпустить в желаемом объёме не получилось – вместо 7 ед. выпустили 6 (не хватило 2-го ресурса; его «экономия» – цель более высокого приоритета).
В заключение в качестве примера составления модели задачи ЦП составим модель ещё одной задачи.
Пример 5.2. Администрация города планирует расширить спортивную базу. На эти цели в городском бюджете выделено 5,4 млн руб. Было запланировано дополнительно построить четыре типа спортивных сооружений: теннисные корты, плавательные бассейны, микростадионы (атлетические площадки) и гимнастические залы. Данные относительно этих проектов следующие (таблица 5.4).
Таблица 5.4 – Информация о строящихся объектах
| Типы сооружений | Ожидаемый спрос | Стоимость (тыс. руб.) | Требуемая площадь (га) | Ожидаемое использование (чел. в неделю) |
| Теннисный корт Плавател. бассейн Министадион Гимнастич. зал | 1 200 | 0,8 2,0 3,2 1,6 | 1 000 2 000 1 500 |
Решение. В городе для этих целей выделено 20 га свободных площадей, но при необходимости эта площадь может быть увеличена. При реализации этого проекта администрация ставит следующие цели в порядке их важности:
1) уложиться в отведённую бюджетом сумму;
2) построенные спортивные сооружения должны обеспечить не менее 14 000 посещений в неделю;
3) по возможности удовлетворить ожидаемый спрос на спортивные сооружения. При формировании целевой функции для этих целевых ограничений использовать веса, пропорциональные ожидаемому использованию;
4) при осуществлении проекта по возможности не занимать более отведённого свободного пространства в 20 га.
При составлении модели этой задачи будем иметь в виду, что ограничения при формулировке целей не категоричные и могут быть как пере-, так и недовыполнены.
Переменные задачи: х1, х2, х3, х4 – соответственно количество построенных сооружений: теннисных кортов, плавательных бассейнов, атлетических площадок и гимнастических залов.
Все ограничения будут целевыми, системных ограничений нет.
Первая цель – уложиться в отведённую сумму:
120х1 + 600х2 + 480х3 + 1 200х4 + d1 - – d1+ = 5 400.
Минимизируем «перерасход»: min Z = P1 d1+.
Вторая цель – не менее 14 000 посещений в неделю:
500 x1 + 1 000x2 + 2 000x3 + 1 500x4 + d2 - – d2+ = 14 000
Минимизируем «недопосещения». С учётом первой цели имеем:
min Z = P1d1+ + P2d2 -.
Реализация третьей цели потребует выполнения 4 ограничений по каждому виду сооружений:
x1 + d3-– d3+ = 8;
x2 + d4-– d4+ = 3;
x3 + d5-– d5+ = 3;
x4 + d6-– d6+ = 2.
Минимизируем «недовыполнение». Это третья по важности цель, поэтому в целевой функции все 4 слагаемых будут иметь коэффициент Р3, но с разными весами:
min Z = P1d1+ + P2d2- + 0,5P3d3- + P3d4- + 2P3d5- + 1,5P3d6-.
Четвёртая цель: 0,8x1 + 5x2 + 3,2x3 + 1,6x4 + d7- – d7+ = 20.
Целевая функция с учётом всех целей:
min Z = P1d1+ + P2d2- + 0,5P3d3- + P3d4- + 2P3d5- + 1,5P3d6- + P4d7+.
Итак, модель задачи примет вид:
Найти min Z = P1d1+ + P2d2- + 0,5P3d3- + P3d4- + 2P3d5 - + 1,5P3d6- + P4d7+
при условии, что
120x1 + 600x2 + 480x3 + 1200x4 + d1 - – d1+ = 5 400,
500x1 + 1 000x2 + 2 000x3 + 1 500x4 + d2 - – d2+ = 14 000,
x1 + d3 - – d3+ = 8,
x2 + d4 - – d4+ = 3,
x3 + d5 - – d5+ = 3,
x4 + d6 - – d6+ = 2,
0,8x1 + 2x2 + 3,2x3 + 1,6x4 + d7 - – d7+ = 20.
xj ³ 0 (j =  ); di -, di+ ³ 0 (i =
); di -, di+ ³ 0 (i = 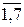 ).
).
Если эту задачу решать обычным симплексным методом, то весам Pi надо придавать конкретные значения, но учитывать, что P1 >> P2 >>…>> P7. Разработаны специальные программы для решения таких задач. Реализуя одну из них (программа QM for Window), получим следующее оптимальное решение (таблица 5.5):
Таблица 5.5 – Решение задачи из примера 5.2.
 (Целевое программирование)
(Целевое программирование)

x1 = 8, x2 = 3, x3 = 3, x4 = 1, d2+ = 500, d6- = 1, d7+ = 3,6. (d7+ = –653 994 – это закодированное число 3,6 – оно указано в строке Priority 4). Указанное недовыполнение (Nonachievement) в строке Priority 3, равное 1,5 – это с учётом весового коэффициента в целевой функции при 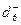 ).
).
Итак, на выделенные средства можно построить 8 теннисных кортов, 3 плавательных бассейна, 3 министадиона и один гимнастический зал. Как видим, четвёртая цель недовыполнена на 1 (d  = 1), т.е. вместо двух запланированных будет построен один гимнастический зал. Вторая цель перевыполнена (d2+ = 500), т.е. вместо 14 000 посещений возможны 14 500. Перевыполнена так же 4-я цель (d7+ = 3,6), т.е. вместо отведённых 20 га под эти спортивные сооружения потребуется 23,6 га.
= 1), т.е. вместо двух запланированных будет построен один гимнастический зал. Вторая цель перевыполнена (d2+ = 500), т.е. вместо 14 000 посещений возможны 14 500. Перевыполнена так же 4-я цель (d7+ = 3,6), т.е. вместо отведённых 20 га под эти спортивные сооружения потребуется 23,6 га.
Глава 6. Методы сетевого планирования и управления
Методы сетевого планирования позволяют осуществить анализ комплекса работ, который включает в себя большое число взаимосвязанных операций. Можно определить вероятную продолжительность выполнения всех работ, их стоимость, возможные размеры экономии времени или денежных средств, а также то, выполнение каких операций нельзя отсрочить, не задержав при этом срок выполнения проекта в целом. Немаловажным является и проблема обеспечения ресурсами. Методы сетевого анализа могут быть использованы при составлении календарного плана выполнения операций, удовлетворяющего существующим ограничениям на обеспечение ресурсами.
Анализ любого проекта осуществляется в три этапа:
1. Расчленение проекта на ряд отдельных работ (или операций), из которых затем составляется логическая схема.
2. Оценка продолжительности выполнения каждой операции; составление календарного плана выполнения проекта и выделение работ, которые определяют завершение выполнения проекта в целом.
3. Оценка потребностей каждой операции в ресурсах; пересмотр плана выполнения операций с учётом обеспечения ресурсами либо
перераспределение денежных или других ресурсов, которое улучшит план.
После того как составлен список, логическая последовательность выполнения операций может быть проиллюстрировала с помощью графа. Существуют различные типы графов, но наиболее широкое применение получили, так называемые вершинные и стрелочные графы.
Date: 2015-10-18; view: 911; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |