Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Аукцион
1. На продажу выставляется произвольный треугольник.
Дать определение треугольника.
Ответ: треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, соединенных отрезками.
2. Продается площадь.
Дать определение.
3. Какую формулу лучше использовать при нахождении площади треугольника.
Задачи (по уровням).
I.
1. Основание треугольника 12 см, его высота – 7 см. Найти площадь треугольника.
2. Катеты прямоугольного треугольника 5 см и6 см. Найти его площадь.
3. Основание треугольника 9 см, а угол между ним и боковой стороной, равной 8 см, равен 30 градусов. Найти площадь треугольника.
II.
1. В прямоугольном треугольнике KMN медиана NP = 10см, а его площадь равна 280 кв. см. Найдите расстояние от середины катета NK до гипотенузы КМ. (При решении этой задачи необходимо помнить, что понятие окружности, описанной около треугольника, учащимся еще неизвестно. В этом случае можно воспользоваться свойствами средней линии треугольника и параллельных прямых).
2. Основание треугольника 12 см. Проекция боковой стороны на основание равна 5 см. Найти площадь треугольника, если известно, что угол между данной боковой стороной и ее проекцией равен 45 градусов.
III.
1. Проекции боковых сторон треугольника равны 6см. Найти площадь треугольника, если один из острых углов этого треугольника равен 45 градусов. (Задачу решить двумя способами).
2. В треугольнике две стороны равны 2см и 4 см. Высота треугольника, проведенная на меньшую из данных сторон, равна 5 см. Что можно сказать о величине высоты, проведенной на большую сторону? Найдите эту высоту.
3. Выразите площадь треугольника через его стороны а, b, с и радиус вписанной окружности r. Сделайте чертеж к задаче.
Билет № 26. Теорема Дезарга.
В проективной геометрии фигуры называются конфигурациями.
Рассмотрим на проективной плоскости P2 три точки A, B, C, не лежащие на одной прямой. Соединим эти точки прямыми. Полученная конфигурация называется трехвершинником (в элементарной геометрии - треугольник). Точки A, B, C – вершины, а прямые, их соединяющие, называются сторонами.
Рассмотрим два трехвершинника, которые могут располагаться в одной плоскости, а могут и не располагаться (обозначим Δ, т.е. ΔABC ΔA’B’C’). Имеет место следующая теорема.
Теорема Дезарга (прямая). Если три прямые, соединяющие соответствующие вершины двух трехвершинников, пересекаются в одной точке, то соответствующие стороны этих трехвершинников пересекаются в трех точках, лежащих на одной прямой.
Док-во: Вектор, порождающий некоторую точку проективной плоскости будем обозначать 
.
Если три точки колинеарны (т.е. лежат на одной прямой) то они порождаются тремя компланарными векторами (т.е. линейнозависимыми).
Рассмотрим три точки A, A’, S. Эти точки колинеарны 
векторы, их порождающие 
, 
, 
– линейнозависимые (т.е. один из этих векторов выражается через два других). Тоже самое относится к тройкам точек B,B’,S и C’,C,S. Т.о. имеем три векторных равенства:
Сравнивая равенства системы (1) получаем:
(из 1 и 2)
(из 2 и 3)
(из 1 и 3)
Введем следующие обозначения 
Из системы (2) имеем 
, 
, 
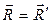(4)
Из системы (3) имеем: точка P 
(AB), точка P’ (A’B’)
точка T (AC), точка T’ (A’C’) (5)
точка R (BC), точка R’ (B’C’)
Учитывая равенство (4) получаем равенство точек P=P’, T=T’, R=R’. (6)
P=M, T=N, R=K (7)
Пользуясь равенством (3) имеем I
II
I
Выполним следующие операции I-II+III (
).
(8)
Перепишем (8) в следующем виде 
(9)
Равенство (9) показывает, что точки M, N, K – колинеарны, т.е. лежат на одной прямой l.
Теорема (обратная). Если прямые, соединяющие соответственные вершины трехвершинников АВС и А'В'С", сходятся в одной точке, то соответственные стороны этих трехвершинников пересекаются в точках, лежащих на одной прямой (существен лишь тот случай, когда трехвершинники АВС и А'В'С' лежат в одной плоскости).
По другому теорема звучит так:
Если два трехвершинника имеют центр перспективы, то они имеют и ось перспективы, и наоборот.
Применение теоремы Дезарга в школьных задачах
Применение теоремы Дезарга в планиметрических задачах основано на интерпретации трёхвершинника проективной плоскости в виде обычного треугольника на евклидовой плоскости. Теорему Дезарга в этом случае можно сформулировать так:
Теорема Дезарга. Пусть на плоскости заданы два треугольника А1В1С1 и А2В2С2, соответствующие вершины которых не совпадают и соответствующие стороны не параллельны. Тогда прямые (А1А2), (В1В2) и (С1С2) пересекаются в одной точке тогда и только тогда, когда три точки АВ = (А1В1) Ç (А2В2), ВС = (В1С1) Ç (В2С2) и АС = (А1С1) Ç (А2С2) лежат на одной прямой.
Задача 1. На плоскости заданы два отрезка прямых и точка. С помощью одной линейки провести прямую, проходящую через эту точку и недоступную точку пересечения данных прямых.
Решение: I. Анализ. Пусть заданы отрезки прямых l, m и точка Р. Предположим, что уже проведена искомая прямая х = (PR). Её можно постараться интерпретировать как ось перспективы некоторых двух трёхвершинников, у которых Р = (A1C1) Ç (A2C2) и R = (A1B1) Ç (A2B2), найти точку Q = (B1C1) Ç (B2C2) и провести прямую х = (PQ).
II. Построение. 1) Произвольно выбираем в доступной части плоскости т. S;
2) проводим три прямые b, c, a, одна из которых (именно b) проходит через т. Р, и все три пересекаются в т. S, получая точки А1 = a Ç l, В1 = b Ç l и А2 = a Ç m, В2 = b Ç m;
3) проводим (А1Р), получая т. С1 = (A1P) Ç c, и (А2Р), получая т. С2 = (A2P) Ç c;
4) (В1С1) Ç (В2С2) = Q;
5) x = (PQ). 
S
A1
l B1
С1
R
x Q P
A2 B2
m С2
III. Доказательство. Теорема Дезарга.
IV. Исследование. Задача всегда имеет единственное решение (даже если исходные прямые были параллельны).
МЕТОДИКА 26. Тема: «Основные задачи на построение с помощью циркуля и линейки»
Решить задачу на построение – это значит найти способ построения фигуры, осуществить это построение и доказать, что построенная фигура – фигура, обладающая требуемыми свойствами.
Для начала мы должны описать, что можно делать с помощью линейки и циркуля.
Линейка – инструмент, позволяющий: провести произвольную прямую; провести прямую (произвольную), проходящую через данную точку; провести прямую, проходящую через две данные точки; построить произвольный луч; построить произвольный луч с заданным началом; построить луч с заданным началом, проходящий через заданную точку; построить отрезок с заданными концами.
Циркуль – инструмент, позволяющий: построить произвольную окружность; построить окружность с заданным радиусом; построить окружность с заданным центром и радиусом; отложить данный отрезок на прямой от данной точки.
Цель: Рассмотреть алгоритм основных задач на построение с помощью циркуля и линейки: деление отрезка пополам, построение перпендикуляра к данной прямой.
Общий прием решения задач на основе деятельностного подхода
1. Изучить содержание задачи.
2. Проверить (вспомнить), есть ли общий прием (алгоритм, правило) решения задач такого типа (если «да» - использовать его, если «нет» - п.3).
3. Провести общий или специальный анализ-поиск решения.
4. На основе анализа или известного приема (алгоритма) составить план решения данной задачи.
5. Решить задачу по составленному плану.
6. Записать решение с использованием соответствующей символики.
7. Если нужно, проверить или исследовать решение.
8. Рассмотреть другие возможные способы решения, выбрать наиболее рациональный.
9. Записать ответ.
Обобщенный прием решения задач на построение
1. Анализ: на этом этапе предполагается, что задача решена, т.е. искомая фигура построена. Находятся связи между элементами фигуры и данными задачи.
2. Построение: на этом этапе дается алгоритм построения искомой фигуры, при этом используются данные анализа.
3. Доказательство: на том этапе доказывается, что построенная фигура действительно является искомой фигурой.
4. Исследование: изучается вопрос о том всегда ли задача имеет решение и сколько имеет решений.
Урок закрепления знаний (структура)
1. Проверка д.з., уточнение направлений актуализации изучения материала.
2. Сообщение темы, целей и задач урока, мотивация учения.
3. Воспроизведение изученного и его применение в стандартных условиях.
4. Применение приобретенных знаний в новых или измененных условиях.
5. Подведение итогов урока.
6. Постановка д.з.
Билет № 27. Метрические свойства поверхности.
Понятие гладкой поверхности.
Рассмотрим вектор-функцию двух скалярных аргументов 
(1). Областью определения D функции (1), т.е. областью изменения параметров (U,V) является некоторая область плоскости с координатными линиями U и V.
Предположим, что в трехмерном пространстве E3 задана прямоугольная система координат 
. Договоримся все векторы откладывать от начала координат в т.О. Если параметр (U,V) изменяется в области D, то т.М описывает в пространстве некоторое множество V.
Опр. Множество V 
E3, заданное вектор-функцией (1) называется гладкой поверхностью, если вектор-функция (1) удовлетворяет следующим двум условиям:
1) функция 
имеет частные производные любого порядка;
2) для любых значений (U,V) первая производная 
, 
линейно независимыми, т.е. являются не коллинеарными векторами. (не параллельны)
В координатной записи вектор-функция 
.
Ведем следующие обозначения: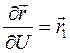 
, 
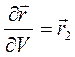
Вектор-функция (1) имеет полный дифференциал 
.
Приведем пример гладкой поверхности: рассмотрим обычную плоскость π, заданную начальной точкой M0, двумя направляющими векторами 
, 
(непараллельные).
Выберем на π произвольно т.М. 
. Имеем равенство 
. Окончательно получаем параметрическое уравнение плоскости π: 
(2)
Проверим выполнимость двух требований:
1) очевидно выполняется, т.к. функция (2) является простейшей линейной функцией;
2) 
, 
.
По условию векторы , - направляющие не коллинеарные не параллельны.
Можно сделать вывод, что обычная плоскость является примером гладкой поверхности.
Первая квадратичная форма поверхности и ее роль.
Рассмотрим поверхность V: 
Имеем 
, 
, 
. Рассмотрим следующие скалярные произведения 
. Введем следующие обозначения: 
, 
, 
. (3)
Учитывая обозначения (3) получаем 
(4)
Выражение, стоящее в правой части равенства (4) представляет собой многочлен второй степени относительно переменных (дифференциалов dU, dV). В курсе алгебры такие многочлены называются квадратичными формами.
Квадратичная форма (4) называется первой квадратичной формой поверхности V.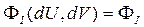 
(5)
Величины g11, g12, g22, найденные по правилу (3) являются коэффициентами формы 
Очевидно, чтобы найти необходимо и достаточно найти ее коэффициенты по формуле (3).
Рассмотрим значение первой квадратичной формы :
1) 
длина линии на поверхности. Рассмотрим на поверхности V, заданной уравнением (1), гладкую линию γ, заданную параметрическим уравнением в криволинейных координатах: 
(6)
Рассмотрим две точки А(t1), B(t2). Найдем длину 
. Её дифференциал 
. Переходя к интегралу проводя элементарные выкладки, используя уравнения (6) получаем: 
.
Итак, первая квадратичная форма позволяет вычислить длину дуги гладкой линии, лежащей на поверхности V.
2) угол между линиями на поверхности. На поверхности V, заданной уравнением (1) рассмотрим две гладкие линии γ1 и γ2, которые пересекаются в некоторой точке М0. Как известно углом между линиями называется угол между касательными к этим линиям в точке пересечения. Дифференцирование вдоль линии γ1 будем обозначать d, а вдоль линии γ2 будем обозначать δ. Т.о. в т.М0 имеем касательные векторы к линии γ1 - 
, к линии γ2 - 
. 
(7)
, т.к. в геометрии угол между линиями считается не тупым, то получаем след. формулу: 
(8)
Воспользуемся формулами (7), чтобы расписать (8) подробно.
2) площадь поверхности. Выберем на поверхности V точку М(U,V). В области D, которая является областью изменения параметров U,V, точке М соответствует 
. Параметру U дадим приращение dU, V – приращение dV. В плоской области D получим прямоугольник 
. На поверхности Vэтому прямоугольнику соответствует криволинейный четырехугольник.
В т.М рассмотрим дифференциалы вектор-функции , т.к. изображение линии на поверхности V яв-ся координатными, то дифференциалы вдоль этих линий имеют такой вид: 
, 
.
На указанных векторах как на сторонах построим параллелограмм, который располагается в касательной плоскости к поверхности V в т.M. Площадь поверхности (V) (S(v)) некоторое число. Из курса мат.анализа известно, что для вычисления некоторой величины нужно найти ее дифференциал, а затем перейти к интегралу. Очевидно: дифференциал S(V) есть площадь бесконечно малой области поверхности V. Т.о. 
(9)
Применяя известные формулы аналитической геометрии 
. Переходя к двойному интегралу получаем следующую формулу для вычисления поверхности V: 
(10)
Воспользуемся известной формулой: 
(11)
Подставляем (10) в (11) получаем: 
Из всего сказанного видно, что первая квадратичная форма к поверхности V позволяет вычислять:
1) длину линии на поверхности;
2) угол между линиями на поверхности;
3) площадь поверхности.
Другими словами: форма позволяет проводить измерения на поверхности, т.е. определяет всю метрику поверхности. Поэтому форма иначе называют основной или метрической формой поверхности V.
МЕТОДИКА 27. 10кл 10-11кл.–старшая шк, предметы алгебра и начала анализа и геометрия.
Методы обуч: наглядные(..), практические(реш-ие зазл упр-ий), словесные, дидак-ие игры(игровые ситуации); по логике излож–дедук м-ды полн; по степени сам-ти-с/р, исслед-кие м-ды.
Юнош-ий возр-т: интелектуал-е воспр-е, символьная нагляд-сть
Цели:
Обуч: ввести пон …; передать уч-ся опред сист матем-х ЗУН. Помочь уч-ся овлад матем-ми идеями, выработать У реш осн типы матем зад, прим-ть теорию на прак.
Разв: разв мировоз(изуч реал действит-ти сред-ми мат), разв позн-ных проц-в, диалект-го мыш-ия, функц-го стиля мышл, разв общеуч-ые умения (раб с книгой).
Восп: восп интерес к мат (истор-ий мат), кул-ру общения, осущ-ть эстет-ое, экол-ое восп-ние, профес-ную ориентацию уч-ся, воспит отд кач лич-ти(аккур, последов-сть, трудолюб, ответственность, настойч-сть и др.)
Урок ознакомления с новым материалом (цель–ввести понятие и устан св-ва или построить прав);
Эт ур: I Орг. мом (сообщ-е темы, ц ур. и мот-ция учеб. деят уч-ся).
II Подгот к изуч нов. мат (повт-е, актуализация баз-х З).
III Ознак с нов. мат.
IV Первич осмыс и закрепл изуч. мат-ла.
V Постан д/з.
VI Подвед ит ур.
Мет-ка изуч пон. 1 Эт – подгот. На нём происх воспр-ие мат-ла, и возник представ-ия, так же н/о показ необх-сть изуч вновь вводим-х пон. Метод-кие приёмы: наблюд, опыт, прак-кая раб, истор-кий обзор, подвод задачи.
2 Эт – основной – определение понятий. Метод-кие приёмы: выявить лог-кую стр-ру опр-ия (термин, род, вид); сформул-ть опр; мотив-ть термин; частные и общие сл понятия; упраж «подведите под понятие»; вывед след-ий; др опр; нахож-е ошибок.
3 Эт – усв пон. Методич. приёмы: установ связь с др. понят; вкл. в клас-цию; провести клас-цию; состав родосл-ую понятия; реш. зад на прим-ие пон; упраж на обобщение и специализацию.
1эт- рассматр-ся зад, привод к опр(по аналогии с кабин)
2эт - термин:угол между прям и пл-тью;род:угол?;видовое отличие:…
3эт -усвоение понятия…классификация:…
В кач-ве средства наглядности м/испол. през MS PowerPoint, различ черт, схемы, макеты и табл.
Билет № 28. Векторное построение геометрии.
Date: 2015-10-18; view: 463; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |