
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Угол между двумя плоскостями
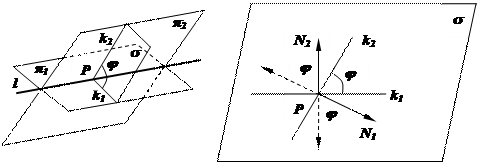 Пусть в пространстве задана декартова система координат. Рассмотрим две плоскости p1, p2 с общими уравнениями Аi×x+Bi×y+Ci×z+Di = 0 (Ai2+Bi2+Ci2 ¹ 0, i = 1, 2). Эти плоскости либо совпадают, либо параллельны, либо пересекаются по прямой. В первых двух случаях величина угла между ними считается равной нулю. В третьем случае при пересечении плоскостей образуются четыре двугранных угла (см. рис.), они попарно вертикальные, и величина меньшего из них называется углом между плоскостями p1 и p2.
Пусть в пространстве задана декартова система координат. Рассмотрим две плоскости p1, p2 с общими уравнениями Аi×x+Bi×y+Ci×z+Di = 0 (Ai2+Bi2+Ci2 ¹ 0, i = 1, 2). Эти плоскости либо совпадают, либо параллельны, либо пересекаются по прямой. В первых двух случаях величина угла между ними считается равной нулю. В третьем случае при пересечении плоскостей образуются четыре двугранных угла (см. рис.), они попарно вертикальные, и величина меньшего из них называется углом между плоскостями p1 и p2.
Как вычислять угол между плоскостями? Рассмотрим прямую l пересечения плоскостей p1 и p2 с направляющим вектором a (a; b; g) и произвольной точкой P(x0; y0; z0) Î l. Тогда величина угла Ð (p1, p2) = j равна углу Ð (k1, k2) между двумя прямыми k1 и k2, перпендикулярными прямой l и проходящими через т. P в плоскостях pi (i = 1, 2). Как было отмечено при выводе нормального уравнения плоскости, для любой плоскости с общим уравнением A×x+B×y+C×z+D = 0 вектор N (A; B; C) перпендикулярен этой плоскости (т.е. перпендикулярен любому направленному отрезку с концами в этой плоскости). Поэтому для плоскости s, проходящей через прямые k1, k2 в качестве вектора N можно взять направляющий вектор a прямой l, перпендикулярный обеим прямым k1 и k2. Таким образом, s имеет общее уравнение вида a×x+b×y+g×z+D = 0, где D = –a×x0–b×y0–g×z0 получается из условия P(x0; y0; z0) Î s.
С другой стороны, векторы Ni (Ai; Bi; Ci), перпендикулярны плоскостям pi (i = 1, 2), а значит и прямой l. Поэтому плоскость с направляющими векторами N1, N2 и проходящая через т. P совпадает с s. Кроме того, из условий N1 ^ k1, N2 ^ k2 следует, что углы Ð (k1, k2) и Ð ( N1, N2 ) с общей вершиной P в плоскости s имеют соответственно перпендикулярные стороны. Значит либо j = Ð (k1, k2) = Ð ( N1, N2 ) и cos j = cos Ð ( N1, N2 ), либо j = Ð (k1, k2) = p – Ð ( N1, N2 ) и cos j = – cos Ð ( N1, N2 ). В любом случае cos j = = |cos Ð ( N1, N2 )|. Таким образом, получены формулы:

Эти формулы справедливы и в случае коллинеарных векторов N1, N2, т.е. когда плоскости p1 и p2 совпадают или параллельны. Особенно просто вычисляется угол между плоскостями, заданными нормальными уравнениями Аi×x+Bi×y+Ci×z+Di = 0 (Ai2+Bi2+Ci2 = 1, i = 1, 2): Ð (p1 , p2) = arc cos |A1×A2+B1×B2+C1×C2 |.
Следствие (о перпендикулярности плоскостей). Плоскости p1 и p2, заданные в некоторой декартовой системе координат общими уравнениями Аi×x+Bi×y+Ci×z+Di = 0 (Ai2+Bi2+Ci2 ¹ 0), i = 1, 2, перпендикулярны (т.е. Ð (p1, p2) =  ) тогда и только тогда, когда A1×A2+B1×B2+C1×C2 = 0.
) тогда и только тогда, когда A1×A2+B1×B2+C1×C2 = 0.
Двугранный угол — пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями.
Полуплоскости называются гранями двугранного угла, а их общая прямая — ребром.
Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.
У всякого многогранника, правильного или неправильного, выпуклого или вогнутого, есть двугранный угол на каждом ребре.
 Расстояние от точки до плоскости. Пусть задана точка M(u; v; w)Î E3 и плоскость p с нормальным уравнением A×x+B×y+C×z+D = 0 (A2+B2+C2= 1). Тогда расстояние r(M, p) от точки M до плоскости p – это min{ MX | X Î p}, и из рисунка видно, что этот минимум достигается при X = Mp (в прямоугольном треугольнике катет короче гипотенузы). Таким образом, r(M, p) = MMp – расстоянию от точки до её проекции на плоскость p. Для нахождения этого расстояния воспользуемся результатами вычислений, проведённых при решении задачи § 8. Имеем
Расстояние от точки до плоскости. Пусть задана точка M(u; v; w)Î E3 и плоскость p с нормальным уравнением A×x+B×y+C×z+D = 0 (A2+B2+C2= 1). Тогда расстояние r(M, p) от точки M до плоскости p – это min{ MX | X Î p}, и из рисунка видно, что этот минимум достигается при X = Mp (в прямоугольном треугольнике катет короче гипотенузы). Таким образом, r(M, p) = MMp – расстоянию от точки до её проекции на плоскость p. Для нахождения этого расстояния воспользуемся результатами вычислений, проведённых при решении задачи § 8. Имеем
Mp((1–A2)×u–A×B×v–A×C×w–A×D; –A×B×u+(1–B2)×v–B×C×w–B×D; –A×C×u–B×C×v+(1–C2)×w–C×D).
Поэтому r(M, p) = MMp =  =
= 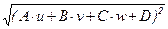 = = |A×u+B×v+C×w+D|.
= = |A×u+B×v+C×w+D|.
В общем случае, когда плоскость задана не нормальным, а общим уравнением, для перехода к нормальному уравнению нужно поделить все коэффициенты общего уравнения на  . Таким образом, получится формула r(M, p) =
. Таким образом, получится формула r(M, p) = 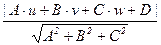 .
.
МЕТОДИКА 23. Тема: «Прямоугольная система координат в пространстве»
11кл 10-11 кл. –старшая шк, предметы алг и нач ан и геометрия. М-ды обуч: наглядные(..), практические(реш-ие зазл упр-ий), слов, дидак-ие игры(игр сит-ии); по логике излож–дедук м-ды полн; по степени сам-ти-с/р, исслед-кие м-ды.Обуч: ввести пон прямоуг сист коорд в пр-ве; выраб-ть умение строить т. по задан ее коор-там; выраб ум нах-ть коор-ты т., изображ-ой в задан сист коор-т. Разв: разв мировоз(изуч реал действит-ти сред-ми мат), разв позн-ных проц-в, диалект-го мыш-ия, функц-го стиля мышл, разв общеуч-ые умения (раб с книгой).Восп: восп интерес к мат (истор-ий мат), кул-ру общения, осущ-ть эстет-ое, экол-ое восп-ние, профес-ную ориентацию уч-ся, воспит отд кач лич-ти(аккур, последов-сть, трудолюб, ответственность, настойч-сть и др.)Ур. ознак с нов. мат(цель–ввести понятие и устан св-ва или построить прав); Эт ур:I Орг. мом (сообщ-е темы, ц ур. и мот-ция учеб. деят уч-ся).II Подгот к изуч нов. мат (повт-е, актуализация баз-х З).III Ознак с нов. мат.IV Первич осмыс и закрепл изуч. мат-ла.V Постан д/з.VIПодвед ит ур.При изуч нов мат-ла д/достиж мот-ции м/создать проблем сит-ию, столк уч-ся с труд, кот они не м/раз-ть при пом имеющ у них запаса З; сталк-сь с труд, они убежд в необх получ нов З или прим стар в нов сит. М-ды мотив: 1.разнооб виды деят-ти 2.яркость эмоц-ть излож мат 3.подбор посильных зад,созд-ие усл для выбора зад разного ур-ня слож и возм-ть скоррек-ть этот выбор в сл неудачи или успеха 4.оперир-ие ранее изуч мат-ом 5. Индивид оцен-ие В кач-ве сред нагляд м/испол презент MS PowerPoint, различ чертежи, схемы, макеты и табл. Пер изуч темы уч-ся м/прочит небол истор-ую справ.
Цели:
Образовательные: -ввести понятие прямоугольной системы координат в пространстве;
- выработать умение строить точку по заданным ее координатам;
- выработать умение находить координаты точки, изображенной в заданной системе координат.
Развивающие: -развитие мировоззрения;
- развитие логического мышления (в форме понятий, суждений, умозаключений);
- развитие геометрического и абстрактного мышления, речи, памяти.
Воспитательные: -воспитание интереса к математике через задачи, занимательные задачи, дидактические игры;
- воспитание отдельных качеств личности: аккуратности, точности, наблюдательности, самостоятельности.
Тип урока: урок изучения нового материала.
Примерный план урока
1.Перед изучением темы учащимся можно прочитать небольшую историческую справку: прямоугольные употреблялись в геометрии еще до начала нашей эры. Древний математик александрийской школы Апполоний Пергский (живший в III – II вв. до н.э.) уже пользовался прямоугольными координатами.
Впервые идея координатного метода была систематически развита Пьером Ферма и Рене Декартом. В их формулировках расстояния до координатных осей могли быть только положительными числами или нулем. Важная идея о том, что одно или оба эти расстояния можно также считать и отрицательными, принадлежит Исааку Ньютону. Г.В.Лейбниц первым назвал эти расстояния «координатными»
Таким образом, открытие декартовых координат не принадлежит Декарту. Декарт построил аналитическую геометрию, а в ней, как в фокусе, сошлись математические открытия медленно, с трудом слагавшиеся в течение тысячелетий. Работа Декарта «La Geometric», в которой излагались основные идеи аналитической геометрии на плоскости, была опубликована в 1637г.
- Объяснить правило задания прямоугольной системы координат в пространстве: прямоугольная система координат в пространстве задана, если выбрана точка – начало координат, через эту точку проведены три попарно перпендикулярные прямые, на каждой из которых выбрано направление (оно обозначается стрелкой), и задана единица измерения отрезков.
- Используя рис 114 учебника, обратить внимание на обозначения и названия осей координат в пространстве. Сопоставить эти обозначения с соответствующими обозначениями осей координат на плоскости, известными из курсов алгебры и геометрии 7 – 9 классов. (см.: Атанасян Л.С. и др. Геометрия 7-9. М.: Просвещение, 1996 и послед изд.)
- Подчеркнуть, что в прямоугольной системе координат каждой точке М пространства соответствует тройка чисел, которые называются ее координатами. Они определяются аналогично координатам точек на плоскости. Можно привести пример, что любую точку Земли можно полностью охарактеризовать широтой, долготой и высотой над уровнем моря.
Для определения координат точки М в пространстве через эту точку проводят три плоскости, перпендикулярные к осям координат. Затем, используя точки М1, М2, М3 пересечения этих плоскостей с осями координат (рис. 115 учебника), находят координаты точки М.
На уроке полезно выполнить упражнения двух типов: на нахождение координат данной точки по чертежу и на построение точки по заданным ее координатам. Для этого можно использовать рис. 116 учебника. Например, для нахождения координаты точки А на этом рисунке, проводим через данную точку перпендикуляр к плоскости ОXY (обозначим его АА1), а затем через точку А1 – перпендикуляры к осям ОХ и OY (обозначим их А1М1 и А1М2). Основания перпендикуляров (точки М1 и М2) дают возможность найти абсциссу и ординату точки А, а длина перпендикуляра АА1 дает аппликату точки А.
Следует объяснить, почему найденные таким образом абсцисса, ордината и аппликата точки А соответствуют данному выше определению координат точки: плоскость АА1М1 перпендикулярна к оси OХ, плоскость АА1М2 перпендикулярна к оси OY, а плоскость, проходящая через точку А и перпендикулярная к оси OZ, пересекает ось ОZ в точке М3, такой, что OM3=АА1, поэтому точки М1, М2, М3 и есть те самые точки, которые позволяют найти координаты точки А.
- Необходимо уделить внимание нахождению координат точек, лежащих в координатных плоскостях или на осях координат. Если точка М(x, y, z) лежит в плоскости OYZ, то y =0
- Для закрепления навыков нахождения координат точек и построение точек по их заданным координатам можно дать задания: 1. Построить по координатам; 2. По рисунку найти координаты вершин фигуры.
Например, построить по координатам:
| (1; -3; 0) | (-2,5; 5,5; 0) | (5; 4; 0) |
| (-1; -3; 0) | (-1; 6; 0) | (5,5; 3; 0) |
| (-2; -2; 0) | (1; 6; 0) | (4; 2; 0) |
| (-3; -1; 0) | (2,5; 5,5; 0) | (3; 1; 0) |
| (-3; 1; 0) | (1,5; 5; 0) | (3; -1; 0) |
| (-2; 2; 0) | (1; 4; 0) | (2; -2; 0) |
| (-1; 3; 0) | (1; 3; 0) | (1; -3; 0) |
| (-1; 4; 0) | (2; 2; 0) | (1,5; 5; 0) |
| (-1,5; 5; 0) | (3; 4; 0) | (-1,5; 5; 0) |

Билет № 24. Движение плоскости.
Движением плоскости называется такое ее преобразование, которое сохраняет расстояния между точками (иногда движение называют перемещением). Всякое движение сохраняет длины отрезков, углы между прямыми и площади фигур.
Основные виды движения плоскости:
1. Параллельный перенос. Параллельным переносом плоскости на вектор а называется отображение плоскости T a: E2 ® E2, при котором каждая точка плоскости сдвигается на вектор а, т.е. T a (M) = M¢, причём  = a.
= a.
Запишем координатные формулы этого отображения в некоторой декартовой системе координат: если a (a; b), M(x; y), M¢(x¢; y¢), то  (x¢ –x; y¢ –y) = a (a; b), откуда находим:
(x¢ –x; y¢ –y) = a (a; b), откуда находим:

Ясно, что это движение первого рода (с матрицей  =
= 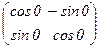 ).
).
2. Поворот. Пусть на плоскости зафиксирована точка С Î Е2. Отображение плоскости RСj: E2 ® E2 называется поворотом с центром в точке С на угол j, если для любой точки M Î E2 и её образа M¢ = RСj(M) направленный отрезок  получается из направленного отрезка
получается из направленного отрезка  поворотом вокруг точки С на угол j. При этом, если j ³ 0, то поворот осуществляется против часовой стрелки, а в случае j < 0 он выполняется по часовой стрелке.
поворотом вокруг точки С на угол j. При этом, если j ³ 0, то поворот осуществляется против часовой стрелки, а в случае j < 0 он выполняется по часовой стрелке.
Зафиксируем на плоскости систему декартовых координат и выведем координатные формулы поворота. Пусть вначале С – начало координат.
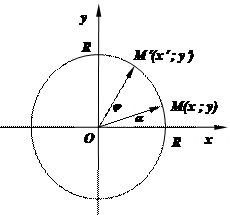
Тогда точки M и M¢ лежат на одной окружности с центром в т. О и радиусом R = OM. Поэтому x2 + y2 = R2,  +
+  = 1, и значит, найдётся такой угол a, что
= 1, и значит, найдётся такой угол a, что  = cos a,
= cos a,  = sin a, т.е.
= sin a, т.е.  . Поэтому
. Поэтому  , и раскрывая по формулам тригонометрии получим:
, и раскрывая по формулам тригонометрии получим:  .
.
Таким образом, получены следующие координатные формулы вращения относительно начала координат:

В общем случае центр вращения имеет координаты С(x0; y0). Поэтому поворачивается на угол j вектор 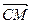 (x–x0; y–y0 ) и переходит в вектор
(x–x0; y–y0 ) и переходит в вектор  (x¢–x0; y¢–y0 ). Подставляя эти координаты в выведенные формулы, получим:
(x¢–x0; y¢–y0 ). Подставляя эти координаты в выведенные формулы, получим:
 или
или  .
.
Итак, получены общие формулы вращения на угол j вокруг произвольного центра С(x0; y0 ):
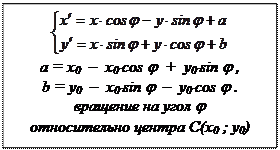
Полученные формулы показывают, что поворот является движением первого рода (с матрицей  ).
).
3. Симметрия относительно точки. Пусть на плоскости задана фиксированная точка О Î E2. Отображение SO: E2 ® E2 называется симметрией с центром в точке О, если для любой точки M Î E2 и её образа M¢ = SO(M) выполняется равенство  = –
= –  .
.
Координатные формулы этого преобразования получаются легко: если в некоторой аффинной системе координат O(x0; y0 ), M(x; y), M¢(x¢; y¢), то  (x–x0; y–y0 ) = = –
(x–x0; y–y0 ) = = –  (x¢–x0; y¢–y0 ) Û
(x¢–x0; y¢–y0 ) Û  Û
Û  .
.
Таким образом, получены координатные формулы для симметрии относительно точки:

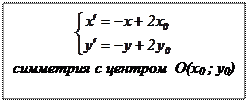
Эти формулы показывают, что симметрия с центром О является движением первого рода (с ортогональной матрицей 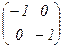 =
=  ) и совпадает со вращением вокруг т. О на угол p (сверьте формулы!!!). Итак, SO = ROp.
) и совпадает со вращением вокруг т. О на угол p (сверьте формулы!!!). Итак, SO = ROp.
 4. Симметрия относительно прямой. Пусть на плоскости задана фиксированная прямая l. Отображение Sl: E2 ® E2 называется симметрией относительно прямой l, если для любой точки M Î E2 её образ M¢ = Sl(M) симметричен M относительно прямой l. Это значит, что (MM¢) ^ l и M¢ симметрична M относительно точки P = (MM¢) Ç l (см. рис.).
4. Симметрия относительно прямой. Пусть на плоскости задана фиксированная прямая l. Отображение Sl: E2 ® E2 называется симметрией относительно прямой l, если для любой точки M Î E2 её образ M¢ = Sl(M) симметричен M относительно прямой l. Это значит, что (MM¢) ^ l и M¢ симметрична M относительно точки P = (MM¢) Ç l (см. рис.).
Пусть в некоторой декартовой системе координат прямая l задана общим уравнением A×x+B×y+C = 0 (A2+B2 ¹ 0), M(x0; y0 ). Тогда, как известно, a (–B; A) – направляющий вектор этой прямой, а n (A; B) ^ a. Поэтому параметрическое уравнение прямой (MM¢) имеет вид  (t Î R ), и можно найти координаты точки P: A×(x0+A×t) + B×(y0+B×t) + C = 0 Û t = –
(t Î R ), и можно найти координаты точки P: A×(x0+A×t) + B×(y0+B×t) + C = 0 Û t = –  . Таким образом, получаем P(x0 – A×
. Таким образом, получаем P(x0 – A×  ; y0 – B×
; y0 – B×  ). Используя выведенные ранее координатные формулы симметрии относительно точки P, отсюда находим:
). Используя выведенные ранее координатные формулы симметрии относительно точки P, отсюда находим:
M¢(–x0 + 2×(x0 – A×  ); –y0 + 2×(y0 – B×
); –y0 + 2×(y0 – B×  )) =
)) =
= M¢(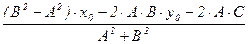 ;
;  ).
).
Используя привычные обозначения M(x; y), M¢(x¢; y¢), получим

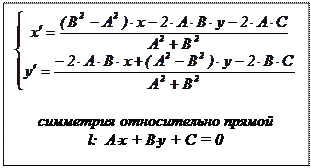
Ясно, что матрица U = 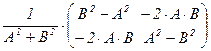 этого аффинного преобразования ортогональна и поэтому имеет вид
этого аффинного преобразования ортогональна и поэтому имеет вид  для некоторого угла j, определяемого условиями
для некоторого угла j, определяемого условиями  . В частности, для прямой l с уравнением y = 0 имеем U =
. В частности, для прямой l с уравнением y = 0 имеем U =  =
=  . Таким образом, симметрия Sl относительно прямой l является движением второго рода.
. Таким образом, симметрия Sl относительно прямой l является движением второго рода.
5. Скользящая симметрия. Это преобразование плоскости Sl, v является композицией двух движений – симметрии относительно прямой l и параллельного переноса на вектор, коллинеарный направляющему вектору этой прямой: Sl, v = T v ×Sl (см. рис.).
Из рисунка видно, что порядок, в котором берётся композиция преобразований в скользящей симметрии несущественен: T v ×Sl = Sl×T v.
 Ясно, что скользящая симметрия, будучи композицией движений первого и второго родов, сама будет движением второго рода. Общие координатные формулы скользящей симметрии запишите сами – приведём только формулы для скользящей симметрии относительно оси OX, когда прямая l задаётся уравнением y = 0, а v (a; 0):
Ясно, что скользящая симметрия, будучи композицией движений первого и второго родов, сама будет движением второго рода. Общие координатные формулы скользящей симметрии запишите сами – приведём только формулы для скользящей симметрии относительно оси OX, когда прямая l задаётся уравнением y = 0, а v (a; 0):

Оказывается, что все движения плоскости исчерпываются частными видами движений, рассмотренными выше.
Можно доказать, что любое движение плоскости является одним из указанных видов, т.е. других движений плоскости не существует. В этом заключается классификация движения.
Теорема (о классификации движений). (1) Любое движение первого рода является либо тождественным преобразованием плоскости, либо параллельным переносом на некоторый вектор, либо поворотом относительно некоторого центра на какой-то угол.
(2) Любое движение второго рода есть либо осевая симметрия (симметрия относительно прямой), либо скользящая симметрия.
(3) Любое движение плоскости есть либо тождественное преобразование плоскости, либо параллельный перенос на некоторый вектор, либо поворот относительно некоторого центра на какой-то угол, либо осевая или скользящая симметрия.
Задача. На плоскости даны прямая l и две т. A и B. Построить на l т. C, такую, чтобы l являлась биссектрисой  .
.
Построение: 1. Применим осевую симметрию и найдем для т. А симметричную ей т.А’.
2. Строим прямую ВА’.
3. Находим точку пересечения l  (BA’)=C.
(BA’)=C.
4. Строим прямую СА.
В силу осевой симметрии ΔСАО=ΔСА’О  против равных сторон лежат равные углы, т.е.
против равных сторон лежат равные углы, т.е. 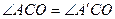 .
.
Date: 2015-10-18; view: 714; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |