
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Модифицированный метод Форда
Этот метод предназначен для нахождения критического пути на сетевом графе (сети). Сеть представляет собой связный бесконтурный орграф G = (X, U) с произвольными весами дуг l (xi, xj), имеющий только одну входную вершину (источник) s Î X, удовлетворяющую условию Г-1(s) = Ø, и одну выходную вершину сток t Î X, для которой Г(t) = Ø.
Сущность метода заключается в одновременном определении для каждой вершины xi графа максимального расстояния l(xi) от источника s и максимального расстояния g(xi) до стока t. Сумма значений l*(xi) и g*(xi) показывает длину максимального пути от s до t, который проходит через вершину xi. Отсюда длина критического пути m[ s, t ] в сети определяется как

Важной особенностью модифицированного метода Форда является отсутствие требования правильной нумерации вершин графа, так как на каждой итерации просматриваются не вершины, а дуги сети. Формальная схема алгоритма приводится ниже.
Алгоритм 2.2 (поиск критического пути
модифицированным методом Форда)
Данные: сеть G = (X, U) c n вершинами и m дугами, где s - входная и
t - выходная вершины сети.
Результаты: длины l*(xi) и g*(xi) максимальных путей m[ s, xi ] и m[ xi, t ], где i = 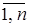 , соответственно.
, соответственно.
Шаг 1 (присвоение начальных значений)
Определить начальные значения l(0)(xi) = 0, g(0)(xi) = 0 для всех вершин xi Î X. Установить номер итерации k = 1.
Шаг 2 (итерационный процесс)
Для всех дуг сети  вычислить новые значения пометок вершин xi и xj:
вычислить новые значения пометок вершин xi и xj:
 (2.2)
(2.2)
где l¢(xi) и g¢(xj) - предыдущие значения пометок.
Шаг 3 (проверка условий окончания)
а) Если k = n, то переход к шагу 4.
б) Если k < n и для всех  выполняются условия:
выполняются условия:
 ,
,
то переход к шагу 4. Иначе присвоить k = k + 1 и переход к шагу 2.
Шаг 4 (получение результатов)
Присвоить l*(xi) = l(k)(xi) и g*(xi) = g(k)(xi) для всех xi Î X. Конец алгоритма.
За один просмотр дуг сети на шаге 2 значения l(xi) и g(xi) для одной и той же вершины могут изменяться многократно (в случае │Г-1(xi)│ > 1 или │Г(xi)│ > 1). Если в результате выполнения очередной итерации хотя бы одна пометка любой вершины принимает новое значение, то процесс повторяется. В предельном случае число итераций может достигать значения n. Поэтому вычислительная сложность алгоритма 2.2 оценивается как O (nm) операций.
Модифицированный метод Форда является наиболее универсальной процедурой, так как его результаты определяют длину критического пути m[ s, t ], а также одновременно длины максимальных путей m[ s, xi ] и m[ xi, t ] для каждой вершины xi сети. Построение любого из указанных путей производится с использованием соотношения (1.2).
Пример 2.1. Применение алгоритма 2.2 демонстрируется для сети G = (X, U), заданной в виде списка дуг и показанной на рис. 2.1.
Результаты работы алгоритма 2.2 представлены в табл. 2.1, где используются следующие обозначения: l i = l(xi); g i = g i (xi). На первой и второй итерациях пометки вершин несколько раз принимают новые значения, поэтому таблица содержит соответствующее число столбцов. На третьей итерации пометки не изменяются, а длина критического пути определяется как l*(x 7) = g*(x 1) = 26.

Рис.2.1. Сеть и ее список дуг для примера 2.1
Таблица 2.1
Результаты применения алгоритма 2.2 для примера 2.1
| Номер вершины | Номер итерации | |||||||||||
| k = 1 | k = 2 | k = 3 | ||||||||||
| l i | g i | l i | g i | l i | g i | l i | g i | l i | g i | l i | g i | |
В заключение следует отметить, что модифицированный метод Форда можно использовать для решения задачи поиска кратчайших путей. Для этого в формулах (2.2) операцию max следует заменить на min.
У П Р А Ж Н Е Н И Я
2.11. Модифицированным методом Форда найти критический путь в графе, представленном на рис. 1.7.
2.12. Составить программу поиска экстремальных путей по алгоритму 2.2.
2.13. Решить задачу из упражнения 1.39 модифицированным методом Форда и сравнить полученные результаты.
2.14. Для графа на рис.1.8 определить пути максимальной длины от x 1 до всех других вершин.
Date: 2015-10-21; view: 595; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |