Метод Флойда

Пусть требуется определить кратчайшие пути m[ x_i, x_j ] между всеми парами вершин x_i и x_j графа G = (X, U). Решение задачи может быть получено n -кратным применением метода Форда - Беллмана (для произвольных весов дуг) или метода Дейкстры (для неотрицательных весов). Предельные оценки вычислительной сложности подобных процедур определяются как O (n ⁴) и O (n ³) операций соответственно. Поэтому в первом случае при большой размерности задачи ее решение крайне затруднительно или даже невозможно.

Более эффективной процедурой поиска всех кратчайших путей m[ x_i, x_j ] для i, j = 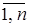является алгоритм Флойда, который применяется к графовым моделям как с неотрицательными, так и с произвольными весами дуг. Если граф содержит контур суммарной отрицательной длины, то алгоритм Флойда фиксирует его существование. При этом предельная оценка трудоемкости для случая произвольных весов дуг составляет O (n ³) операций, а для неотрицательных весов время решения примерно на 50 % меньше по сравнению с n -кратным применением алгоритма Дейкстры [5].

Алгоритм Флойда базируется на использовании последовательности из n преобразований итераций начальной матрицы 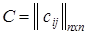весов дуг, элементы которой определяются следующим образом:

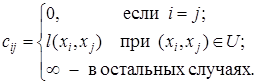
На каждой k -й итерации (k £ n) элементы 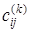матрицы С определяют длины кратчайших путей между каждой парой вершин x_i и x_j при условии, что путь m[ x_i, x_j ] может проходить только через вершины из множества { x ₁, x ₂,..., x_k }. Таким образом, итоговое значение матрицы C после выполнения n итераций показывает искомые значения 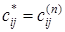длин кратчайших путей m[ x_i, x_j ].

В основе алгоритма Флойда лежат следующие очевидные уравнения:

, (1.8)

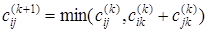. (1.9)

Пусть кратчайший путь m[ x_i, x_j ] может содержать промежуточные вершины из множества { x ₁, x ₂,..., x_{k -1}, x_k }. Тогда второе уравнение показывает, что если этот путь не содержит вершину x_{k +1}, то его длина определяется как 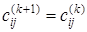. В противном случае путь m[ x_i, x_j ] можно разбить на две части m[ x_i, x_{k +1}] и m[ x_{k +1}, x_j ]. Следовательно, его длина составляет . В целом уравнения (1.8) и (1.9) позволяют легко вычислить длины 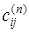кратчайших путей m[ x_i, x_j ] между всеми парами вершин x_i, x_j Î X.

Алгоритм 1.5 (метод Флойда)

Данные: матрица 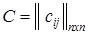весов дуг ориентированного графа G = (X, U); произвольные значения c_ij для (x_i, x_j) Î U.

Результаты: кратчайшие расстояния 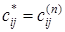между всеми парами вершин (x_i, x_j) Î X.

Шаг 1 (присвоение начальных значений)

Установить номер итерации k = 0.

Шаг 2 (итерационный процесс)

Присвоить k = k + 1. Для всех i ¹ k, удовлетворяющих условию , и для всех j ¹ k, таких, что 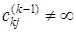, вычислить новые значения

Все другие элементы матрицы C сохранить без изменений, т. е.

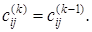
Шаг 3 (проверка условий окончания)

а) Если 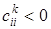, то граф G содержит контур отрицательной длины, проходящий через вершину x_i, и задача не имеет решения. Конец алгоритма.

б) Если 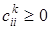и k = n, то решение получено. Конец алгоритма.

в) Если 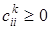и k < n, то переход к шагу 2.

Кратчайший путь m[ x_i, x_j ] можно построить исходя из его длины 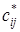следующим образом. Сначала определяется предпоследняя вершина пути 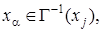предшествующая x_j, по условию . Затем находится вершина 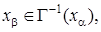для которой 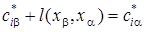и т. д. подобно использованию соотношения (1.2).

В работах [5, 8, 11] представлен метод построения путей m[ x_i, x_j ], основанный на хранении дополнительной информации об индексах вершин, составляющих тот или иной путь. Для этого требуется еще одна матрица 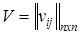, элемент v_ij которой указывает индекс вершины, непосредственно предшествующей x_j в пути m[ x_i, x_j ].

Начальные значения 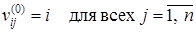присваиваются элементам матрицы V на шаге 1 алгоритма 1.5. Обновление матрицы производится на шаге 2 следующим образом:

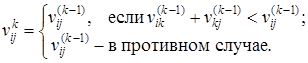
Полученные значения 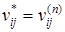позволяют построить кратчайший путь

m[ x_i, x_j ] = (x_i, x_v, …, x _g, x _b, x _a, x_j)

между любой парой вершин, где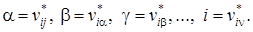

Пример 1.4. Пусть граф G = (X, U) имеет вид, показанный на рис. 1.9. Требуется вычислить расстояния между всеми парами вершин и сформировать матрицу V для построения кратчайших путей.

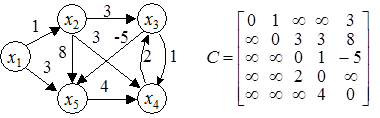
Рис. 1.9. Представление графа G для примера 1.4

На первой итерации алгоритма 1.5 матрицы C ⁽⁰⁾ = C и V ⁽⁰⁾ = V не изменяются, так как элементы 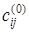, которые могут быть уменьшены, при k = 1 определяются индексами i Î Ø и j Î {2, 3, 4, 5}. Следовательно, C ⁽¹⁾ = C ⁽⁰⁾ и V ⁽¹⁾ = V ⁽⁰⁾.

На второй итерации (k = 2) производится вычисление новых значений для элементов c_ij и v_ij, где i Î {1} и j Î {3, 4, 5}:

При k = 3 могут измениться элементы с индексами i Î{1, 2, 4} и j Î {4, 5}. Результаты работы алгоритма 1.5 на каждой итерации имеют следующий вид, где C ⁽⁵⁾ = C ^* и V ⁽⁵⁾ = V^*:

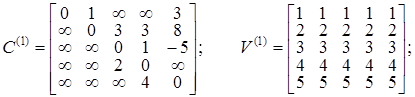
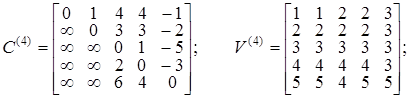
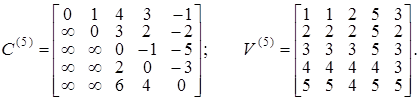
Построение кратчайшего пути m[ x ₁, x ₄], для которого длина определяется как = 3, производится следующим образом. Согласно определению матрицы V элемент 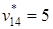показывает индекс предпоследней вершины x ₅ искомого пути. Далее 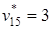, т. е. искомый путь имеет вид m[ x ₁, x ₄] = (x ₁, …, x ₃, x ₅, x ₄). Следующее значение указывает еще одну промежуточную вершину x ₂. Окончательно имеем 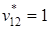и путь m[ x ₁, x ₄] = (x ₁, x ₂, x ₃, x ₅, x ₄).

В заключение следует отметить, что структура матрицы V позволяет легко найти в графе контур суммарной отрицательной длины при его существовании (c _ii < 0) как кратчайший путь вида m[ x_i, x_j ].

У П Р А Ж Н Е Н И Я

1.41. Продолжить решение задачи из примера 1.4 для итераций k =3, 4, 5. Построить кратчайший путь из вершины x ₂ в x ₄ без применения матрицы V.

1.42. Вычислить расстояния между всеми парами вершин для графа, показанного на рис. 1.10,а. Определить кратчайший путь из x ₁ в x ₆ и, наоборот, из x ₆ в x ₁.

1.43. Разработать программу вычисления минимальных расстояний между всеми парами вершин графа по методу Флойда.

1.44. Разработать программу построения кратчайших путей по матрице V.

1.45. Определить контур отрицательной длины для графа, приведенного на рис. 1.10,б.

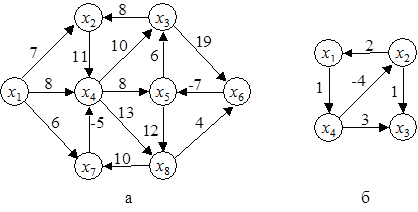
Рис. 1.10. Графы для упражнений: а - 1.42; б - 1.45

Date: 2015-10-21; view: 1725; Нарушение авторских прав