
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные модели и задачи
КРАТЧАЙШИЕ ПУТИ
Основные модели и задачи
Рассмотрим связный ориентированный граф G = (X, U), где X = { x 1, x 2,..., xn } - множество вершин, U = { u 1, u 2,..., um } - множество дуг вида
up = (xi, xj), xi, xj Î X.
Путем в ориентированном графе G называют последовательность дуг m = (u 1, u 2,..., uk), в которой конечная вершина каждой предыдущей дуги совпадает с начальной вершиной следующей дуги. Путь также может определяться как последовательность вершин m = (x (0), x (1), x (2),..., x (p)), соединенных дугами графа. Конечный путь m, для которого начальная вершина x (0) совпадает с конечной x (p), называется контуром. Путь, в котором никакая дуга не встречается дважды, называется простым.
Длиной пути m = (u 1, u 2,..., uk) называют число L (m) = k, равное количеству дуг, составляющих этот путь. Если каждой дуге u = (xi, xj) соответствует некоторое число l (xi, xj), называемое длиной или весом дуги (графы со взвешенными дугами), то длина пути в таком графе определяется как
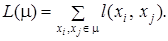
Наиболее часто для заданного графа G = (X, U) требуется определить кратчайший путь m[ s, t ] из некоторой выделенной вершины s (источника) в другую заранее заданную вершину t (сток), где s, t Î X. Если значения
l (xi, xj) ³ 0 рассматривать как стоимости прохождения единицы потока по дугам (xi, xj) Î U, то задачу можно сформулировать следующим образом [2, 8]: определить поток единичной мощности из источника s в сток t, который имеет минимальную стоимость.
Соответствующая задача целочисленного линейного программирования (ЦЛП) заключается в определении значений переменных zij Î {0, 1}, сопоставленных с дугами (xi, xj) Î U и обеспечивающих

при ограничениях
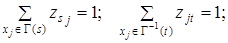

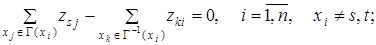
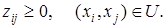
Отметим, что приведенная формулировка задачи поиска кратчайшего пути m[ s, t ] определяет частный случай, для которого длины дуг l (xi, xj) всегда неотрицательны, и может быть решена как задача ЦЛП.
В общем случае при построении кратчайших путей выделяют графовые модели, особенности которых отражены на рис. 1.1.
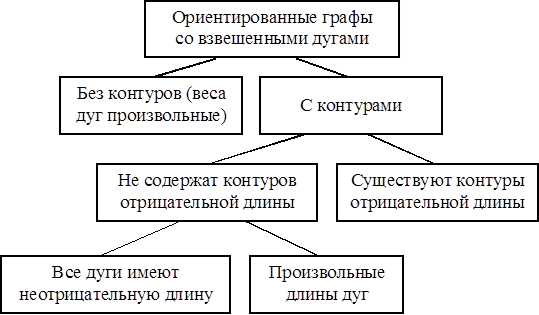
Рис. 1.1. Виды графовых моделей
для задачи поиска кратчайшего пути
Практически для всех указанных на рис. 1.1 разновидностей графов существуют эффективные алгоритмы построения кратчайших путей, учитывающие специфические особенности конкретных моделей. Исключение составляют ориентированные графы, содержащие контуры с суммарной отрицательной длиной (весом). Если такой контур j существует, то при построении любого пути m[ s, t ] на графе, проходящего через вершину
xi Î j, можно получить сколь угодно малую длину L (m) ® -¥ за счет многократного обхода контура j. Таким образом, в этом случае кратчайшего пути m[ s, t ] не существует и можно решать задачу построения кратчайшего простого пути от s к t, которая является значительно более сложной и сводится к нахождению кратчайшего гамильтонова пути [5]. Тем не менее, в работе [1] описан алгоритм поиска простого пути наименьшей длины между вершинами s и t, а в [5] - метод обнаружения контуров суммарного отрицательного веса.
Основные методы решения задачи поиска кратчайшего пути m[ s, t ] на графе G = (X, U) и области их применения показаны в табл. 1.1, где обозначения “-”, “+” и “++” имеют смысл “применение невозможно”, “применение возможно” и “применение целесообразно” соответственно.
Алгоритм Форда - Беллмана является наиболее универсальным и может использоваться для графовой модели любого вида. Однако его применение наиболее целесообразно для графов, в которых существуют контуры положительной длины и веса дуг имеют произвольные значения. Если все дуги (xi, xj)Î U имеют неотрицательные значения l (xi, xj) ³ 0, то более эффективным с точки зрения вычислительной сложности является алгоритм Дейкстры. Для бесконтурных графов наиболее быстро работает алгоритм, основанный на идее динамического программирования и реализованный в методах PERT (Project Evaluation Research Task) и CPM (Critical Path Method). В отечественной литературе наряду с этими обозначениями используются термины СПУ (сетевое планирование и управление) и МКП (метод критического пути) соответственно.
Таблица 1.1
Области применения методов поиска кратчайших путей на графах
| Базовый метод [источники] | Вид графовой модели | Оценка вычислительной сложности | ||
| с контурами положительной длины | без контуров | |||
| произвольные длины дуг | неотрицательные длины дуг | |||
| Алгоритм Форда - Беллмана [3-7, 10-12] | + + | + | + | O (n 3) |
| Алгоритм Дейкстры [1, 2, 5-9, 11] | - | + + | + | O (n 2) |
| Динамического программирования [3-6] | - | - | + + | O (m) |
Непосредственными обобщениями представленной выше задачи о кратчайшем пути являются две следующие задачи.
Задача А. Для заданной начальной вершины s Î X найти кратчайшие пути m[ s, xi ] между s и всеми другими вершинами xi Î X \ s.
Задача В. Определить кратчайшие пути m[ y, z ] между всеми парами вершин y, z Î X.
Практически все методы, позволяющие решить задачу о кратчайшем пути m[ s, t ], обеспечивают также и получение всех кратчайших путей от s к любой вершине xi Î X \ s с небольшими дополнительными вычислительными затратами. Модификации базовых методов для решения задачи А будут показаны в следующих разделах. Задача В может быть решена либо n -кратным применением алгоритмов для задачи А, причем на каждом шаге в качестве s выбираются различные вершины y Î X, либо однократным применением специального алгоритма (например, алгоритма Флойда [6 - 9, 11], обеспечивающего решение задачи В для графов с контурами положительной длины при произвольных весах дуг).
В заключение необходимо отметить, что все перечисленные методы и алгоритмы предназначены для поиска путей в ориентированных графах. Однако, если исходный граф G содержит неориентированные ребра, то для поиска кратчайшего пути можно рассматривать новый граф G ¢, в котором каждое ребро [ xi, xj ] с весом lij заменяется парой противоположно направленных дуг (xi, xj) и (xj, xi) с весами l (xi, xj) = l (xj, xi) = lij соответственно.
У П Р А Ж Н Е Н И Я
1.1. Определить понятия пути, простого пути и контура в ориентированном графе. Привести примеры для заданного графа.
1.2. Как вычисляется длина пути в ориентированном графе при отсутствии и наличии весов дуг?
1.3. Для заданного графа сформулировать задачу поиска кратчайшего пути между двумя фиксированными вершинами в виде задачи линейного программирования. Почему эта задача относится к классу целочисленных и каким методом ее можно решить?
1.4. По каким критериям выполняется классификация графовых моделей для решения задачи поиска кратчайшего пути?
1.5. Почему задача поиска кратчайшего пути для графа с контурами отрицательной длины может не иметь решения? При каких дополнительных ограничениях обычно решают эту задачу?
1.6. Перечислить основные методы решения задачи построения кратчайшего пути и указать виды графовых моделей, где их применение целесообразно, возможно и невозможно.
1.7. Сформулировать задачи, связанные с поиском путей на графах, которые наиболее близки к задаче построения кратчайшего пути m[ s, t ].
1.8. Возможно ли применение перечисленных методов поиска кратчайших путей для неориентированных и смешанных графов?
Date: 2015-10-21; view: 578; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |