Вектори у декартовій системі координат

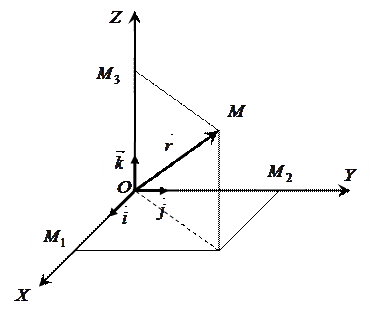
У прямокутній декартовій системі координат розглянемо довільний вектор 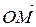(рис..6).

Вектор 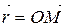називають полярним радіусом-вектором точки М. Спроектуємо цей вектор на координатні осі. Інакше кажучи, розкладемо вектор 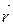на складові вектори за координатними осями. Як показано на рис. 2.6 точки 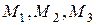– проекції точки 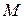на відповідні координатні осі.

Вектори 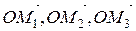– складові вектора 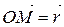за відповідними координатними осями.

Рис. 2.6

Вектор 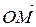є сумою векторів 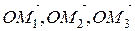, тобто

.

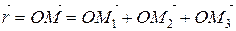(2.3)

Кожний з цих складових векторів можна надати у вигляді: 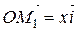, , 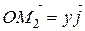, 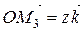де 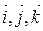– базисні вектори декартової системи координат у просторі. Підставляючи ці значення в (2.3), одержуємо:

,

(2.4)

де 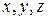– скалярні величини, які називаються координатами радіус-вектора 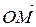у заданому базисі.

Точка 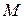має координати свого радіус-вектора 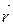, тобто 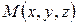. Координати точки у просторі або її радіус-вектор 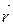однозначно вказують на її положення в просторі відносно вибраної системи координат.

Довільний вектор 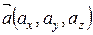можна надати у вигляді:

.

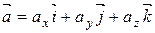(2.5)

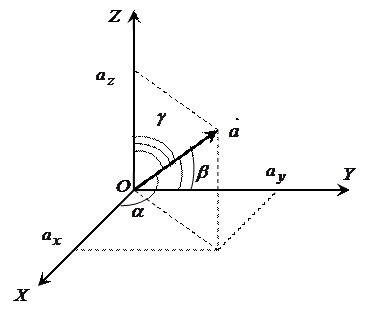
Подання вектора у вигляді суми компонентів (2.5) називається розкладанням вектора за координатним базисом (рис. 2.7).

Довжина (модуль) вектора визначається за формулою

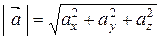.	(2.6)
Рис. 2.7

На рисунку 2.7 вектор утворює з координатними осям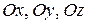и кути відповідно. Тоді називаються напрямними косинусами вектора . Очевидно, напрямні косинуси та модуль вектора повністю визначають положення вектора у просторі. Враховуючи властивості проекції вектора на вісь, маємо:

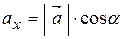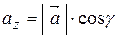, , ;	(2.7)
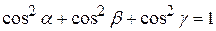
	(2.8)

Лінійні операції над векторами у координатній формі:

Дано вектори та :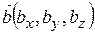

1) додавання та віднімання

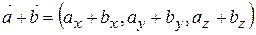;	(2.9)
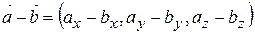;	(2.10)

2) множення вектора на скаляр

.

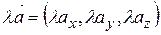(2.11)

Умови колінеарності двох векторів та 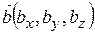визначаються співвідношенням

.

(2.12)

Date: 2015-10-18; view: 421; Нарушение авторских прав