Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Теоремы о базисах
Теорема 1. Пусть е 1 ,…,е п – базис линейного пространства L. Тогда любой вектор а Î L однозначно выражается через базис в виде а = b 1 ×е 1 +…+b п ×е п для некоторых b 1 ,…,b п Î Р.
Доказательство. Пусть а Î L. Так как dim L = п, то п+1 векторов а,е 1 ,…,е п линейно зависимы, то есть $ a,a 1 ,…,a п Î Р, не все равные нулю, такие, что a×а +a 1 ×е 1 +…+a п ×е п =0 L, причем a ¹ 0, так как векторы е 1 ,…,е п линейно независимы. Тогда а=a -1a 1 ×е 1 +…+a -1a п ×е п =b 1 ×е 1 +…+b п ×е п, где b 1 =a -1a 1 ,…, b п =a -1a п.
Докажем однозначность. Пусть а = b 1 ×е 1 +…+b п ×е п =
= g 1 ×е 1 +…+g п ×е п Þ (b 1 -g 1 )е 1 +…+(b п -g п )е п = 0 L Þ b 1 - g 1 =0,…, b п -g п = 0, так как векторы е 1 ,…,е п линейно независимы Þ
b 1 = g 1,…, b п = g п – это и означает однозначность.
ÿ
Теорема 2 (обратная). Пусть е 1 ,…,е п – такая система векторов в L, что любой вектор а Î L однозначно выражается через е 1 ,…,е п в виде а = b 1 ×е 1 +…+b п ×е п для некоторых
b 1 ,…,b п Î Р. Тогда е 1 ,…,е п – базис линейного пространства L.
Доказательство. 1. е 1 ,…,е п – линейно независимая система векторов в L, так как если a 1 ×е 1 +…+a п ×е п = 0 L =
= 0×е 1 +…+ 0×е п, то из однозначности a 1 = 0,…,a п = 0. Следовательно, в L существуют п линейно независимых векторов.
2. Покажем, что в L любые п+1 векторов линейно зависимы.
Пусть а 1 ,…,а п+1 Î L. Тогда а 1 = b 11 ×е 1 +…+b 1п ×е п ,…,
а п+1 =b п+1,1 ×е 1 +…+b п+1,п ×е п. Покажем, что существуют
х 1 ,…,х п+1 Î Р, не все равные нулю, такие, что
х 1 а 1 +…+х п+1 а п+1 = 0. Но х 1 а 1 +…+х п+1 а п+1 =
= (b 11 х 1 +…+b п+1,1 х п+1 )е 1 +…+(b 1п х 1 +…+b п+1,п х п+1 )е п, и однородная система п уравнений с п+1 неизвестным
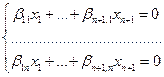имеет ненулевое решение (см. 4.3).
Таким образом, dim L = n, и е 1 ,…,е п – базис в L.
ÿ
Теорема 3. Если е 1 ,…,е п – базис линейного пространства L, то е 1 ,…,е п – максимальная линейно независимая система векторов в L, то есть при добавлении к этой системе любого вектора получится линейно зависимая система векторов.
Доказательство. Так как е 1 ,…,е п – базис, то dim L = n, и из определения размерности следует, что любые п+1 векторов линейно зависимы.
ÿ
Теорема 4 (обратная). Если е 1 ,…,е п – максимальная линейно независимая система векторов в L, то е 1 ,…,е п – базис линейного пространства L.
Доказательство. Пусть а Î L. Так как п +1 векторов
а, е 1 ,…,е п линейно зависимы, то, как и в Теореме 1, вектор а линейно выражается через е 1 ,…,е п. Из линейной независимости векторов е 1 ,…,е п , как и в Теореме 1, следует, что выражение а через е 1 ,…,е п однозначно. Теперь по Теореме 2 мы получаем, что е 1 ,…,е п – базис линейного пространства L.
ÿ
Теорема 5. dim P n = n.
Доказательство. Пусть е 1 =(1,0,0,…,0), е 2 =(0,1,0,…,0),…,
е n =(0,0,0,…,1). Тогда " (a 1 ,a 2 ,…,a n )Î Р n
(a 1 ,a 2 ,…,a n )= (a 1 ,0,…,0)+ (0,a 2 ,…,0)+ …+(0,0,…,a n )=
=a 1 (1,0,…,0)+ a 2 (0,1,…,0)+ …+a n (0,0,…,1)= a 1 ×е 1 +…+a п ×е п и это представление однозначно. Значит, по Теореме 2 е 1 ,…,е п – базис в P n, и dim P n = n.
ÿ
Лекция 14.
Теорема 6. Любую линейно независимую систему векторов в пространстве L можно дополнить до базиса L.
Доказательство. Пусть а 1 ,…,а k – линейно независимая система векторов в L. Если это максимальная линейно независимая система векторов, то а 1 ,…,а k – базис линейного пространства L по Теореме 4. Если это не максимальная линейно независимая система векторов, то существует некоторый вектор а k+1 такой, что а 1 ,…,а k ,а k+1 - линейно независимая система векторов в L. Опять, если это максимальная линейно независимая система векторов, то а 1 ,…,а k+1 – базис линейного пространства L, а если не максимальная, то добавляем вектор а k+2 и т.д. пока не получим максимальную линейно независимую систему векторов, то есть базис.
ÿ
Пусть е 1 ,…,е п – базис линейного пространства L и хÎL. Тогда х = х 1 ×е 1 +…+х п ×е п, и набор (х 1 ,…,х п ) называется координатами вектора х в базисе е 1 ,…,е п .
Упражнение. Доказать, что если (х 1 ,…,х п ) координаты вектора х, а (у 1 ,…,у п ) координаты вектора у в базисе е 1 ,…,е п , то координатами вектора х+у будет набор (х 1 +у 1 ,…,х п +у п ), а координатами вектора a х, aÎ Р, будет набор (a х 1 ,…,a х п ).
Date: 2015-09-25; view: 991; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |