
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема единственности и некоторые следствия из нее
Докажем, что в абсолютной геометрии при данном выборе единичного отрезка $ единственное отображение l:L® R+, удовлетворяющее L1-L3. Обозначим АВ, СД,…- отрезки ÷АВ÷,÷СД÷,…-их длины в выбранной единице измерения.
Теорема (единственность длины в абсолютной геометрии). Если выбран единичный отрезок PQ, то существует не более одного отображения l:L®R+, удовлетворяющего трем аксиомам измерения отрезков.
Для доказательства понадобятся три простые леммы, доказательство которых вы разберете самостоятельно.
Лемма 1 Пусть установлено измерение отрезков с единицей измерения PQ. Если точки А0, А1, А2, …, Аn расположены так, что А0-А1-А2, А1-А2-А3,…, Аn-2- Аn-1-Аn и А0А1 = А1А2 = … = Аn-1Аn = РQ, то ÷А0Аn÷ =n.
Лемма 2 Пусть установлено измерение отрезков. Если АВ<СД, то ÷АВ÷<÷СD÷.
Лемма 3 Пусть установлено измерение отрезков. Если точка O - середина отрезка АВ, то ÷А0÷=÷0В÷= 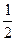 ÷АВ÷
÷АВ÷
Доказательство теоремы (от противного) Пусть l:L®R+ и l/:L®R+ удовлетворяет L1-L3. l(PQ)=l/(PQ)=1 (1)
Т.к. l и l /-различные отображения, то $ отрезок АВ т. что l (АВ)=а, l/ (АВ)=b и а¹b. Пусть b>а. На луче АВ отложим последовательно отрезки АА1, А1А2,…Аn-1Аn, причем n выберем так чтобы А-В-Аn. Аn-1 принадлежит отрезку АВ, т.е. Аn-1 может совпадать с В. По аксиоме Архимеда такое n-$, тогда по лемме 1.








 l(AAn-1)=l/(AAn-1)=n-1 (2)
l(AAn-1)=l/(AAn-1)=n-1 (2)
A An-1 B
l(AAn)=l/(AAn)=n (3)
A B В не может совпадать с Аn-1, т.к отрезок один, а измерения разные. Это противоречит тому, что а¹b. Значит Аn-1-В-АnÞ ААn-1<АВ<ААn l(AAn-1)<l(AB)<l(AAn) или
n-1<a<n n-1<в<n Þв-а<1. Пусть Р1 середина отрезка Аn-1Аn тогда из L2 и L3 Þl(AP1)=l(AAn-1)+l(An-1P1)=n-1+1/2=n-1/2 Аналогично получаем l/(AP1)=n-1/2. Снова получаем, что Р1 не совпадает с В. Либо Аn-1-В-Р1, либо Р1-В-Аn. В первом случае получаем AAn-1<AB<AP1, n-1<a<n-1/2 и n-1<b<n-1/2. Во втором случае: AP1<AB<AAn, и n-1/2<a<n, n-1/2<b<n. В обоих случаях b-a<1/2. Продолжая, получим b-a<1/2k, и этот процесс никогда не остановится в силу условия a¹b. Значит b-a=0 и, поэтому l и l/ совпадают. Ч.т.д.
Теорема 2. Каково бы ни было вещественное число а>0, при данном выборе единичного отрезка $ отрезок, длина которого равна а. (без доказательства)
С помощью этой Тh можно ввести систему координат на прямой, т.е. ввести координаты значит:
Следствие 1 В теориях содержащих абсолютную геометрию можно установить измерение отрезков с произвольно выбранным единичным отрезком. При этом установленное измерение является единственным.
Следствие 2. В теориях Á(åр) Á(åк) при данном выборе единичного отрезка результат процесса измерения отрезков совпадает с тем, который следует из аксиом меры, а в Á(åw) из W3.
§4. Многоугольник и его характеристика (плоский)
Напомним несколько определений.
Опр. 1. Ломаная называется простой, если смежные звенья не лежат на одной прямой и не смежные звенья не имеют общих точек. Если концы ломаной А1А2…Аn А1 и Аn совпадают, то она называется замкнутой: в этом случае звеня Аn-1Аn и А1А2 тоже являются смежными. Простая замкнутая ломанная разделяет множество всех точек плоскости не принадлежащих ломаной, на два подмножества, одно из которых называется внутренней областью, а другое - внешней.
Опр. 2. Объединение простой замкнутой ломаной и ее внутренней области называется простым многоугольником, а сама эта ломанная называется его границей.
Пусть F- многоугольник, А и В - точки на его границе. Соединим точки А и В простой ломаной L, все точки которой, кроме А и В, лежат внутри многоугольника, тогда получим два новых многоугольника F1 и F2: F1ÇF2=L, F=F1ÈF2.
Опр. 3. Многоугольник F в этом случае будем называть суммой многоугольников F1 и F2 и записывать F=F1+F2 (в отличи от объединения).
Опр. 4. Многоугольник F назовем ориентированным, если указан порядок обхода его вершин, обозначаем 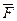 =
= 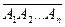 . (Каждый простой многоугольник гомеоморфен двумерной клетке.)
. (Каждый простой многоугольник гомеоморфен двумерной клетке.)
Опр. 5. Пусть F=F1+F2. Ориентированный многоугольник 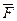 будем называть суммой ориентированных многоугольников
будем называть суммой ориентированных многоугольников 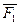 и
и 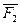 , если ориентации
, если ориентации  ,
, 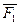 ,
, 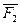 согласованы, т.е. общей стороне приписывается противоположное направление обхода в каждом многоугольнике.
согласованы, т.е. общей стороне приписывается противоположное направление обхода в каждом многоугольнике.
Обозначим через М- множество всех многоугольников евклидовой плоскости s.  единичный вектор ^ s. Пусть
единичный вектор ^ s. Пусть 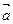 и
и 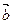 – векторы // s. Смешанное произведение (
– векторы // s. Смешанное произведение (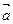 ,
, 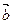 ,
,  ) обозначим через
) обозначим через 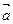 °
° 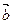 (оно определяется без площади). В направляющем пространстве плоскости s выберем базис (
(оно определяется без площади). В направляющем пространстве плоскости s выберем базис (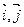 ), так чтобы
), так чтобы 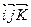 =1, т.е. чтобы он был ориентирован положительно. В базисе (
=1, т.е. чтобы он был ориентирован положительно. В базисе ( ) векторы
) векторы 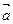 =(а1,а2),
=(а1,а2), 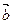 (в1,в2). В
(в1,в2). В 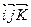
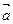 =(а1,а2,0)
=(а1,а2,0) 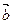 (в1,в2, 0)
(в1,в2, 0)  =(0,0,1) тогда
=(0,0,1) тогда
Свойство 1° 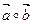 =(
=(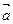 ,
, 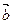 ,
,  )=
)= 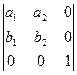 =
= 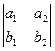 .
.
Следствие 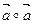 =0
=0
Свойство 2° 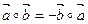
С войство 3° если 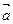 ,
, 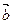 ,
, 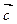 //s, то
//s, то 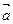 °(
°(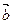 +
+ 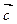 )=
)= 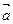 °
° 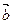 +
+ 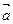 °
° 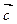 и (
и (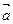 +
+ 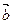 )°
)° 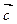 =
= 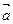 °
° 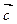 +
+ 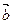 °
° 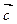 : по свойствам смешанного произведения.
: по свойствам смешанного произведения.
Пусть  - ориентированный n-угольник, ОÎs, положим
- ориентированный n-угольник, ОÎs, положим 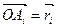 , i=1,…,n.
, i=1,…,n.
Опр. 6. Число 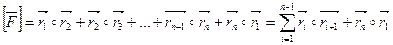 (1)
(1)
Называется характеристикой многоугольника 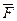 .
.
Если в системе координат О 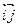 вершины Аi(xi,yi), то (1)
вершины Аi(xi,yi), то (1)
Запишется в виде 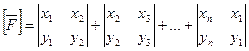 (2)
(2)
Ch 1 Характеристика многоугольника 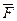 не зависит от выбора т. О на плоскости s.
не зависит от выбора т. О на плоскости s.
Д оказательство: Пусть О/- другая точка плоскости s. 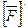 - характеристика многоугольника относительно этой точки. Тогда обозначим
- характеристика многоугольника относительно этой точки. Тогда обозначим 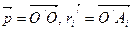 по Опр.6.
по Опр.6.
|
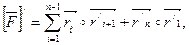 но
но 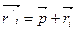 подставляем это в
подставляем это в 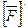 , после несложных преобразований (Пояснить), с учетом свойства 2° и свойства 3° получим, что
, после несложных преобразований (Пояснить), с учетом свойства 2° и свойства 3° получим, что  =
= 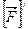 . Что и требовалось доказать.
. Что и требовалось доказать.
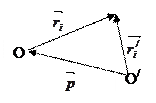 |
Ch 2 Если 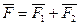 , то
, то 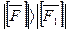 и
и 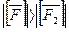 (без доказательства)
(без доказательства)
Сh 3 Если 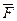 - произвольный многоугольник, то
- произвольный многоугольник, то  , и значит
, и значит 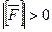 .
.
Доказательство самостоятельно.
Ch 4 Любой многоугольник можно ориентировать так, чтобы его характеристика была положительной.
Доказательство Изменив ориентацию многоугольника на противоположную и заменив нумерацию: 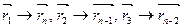 и т. д. из (1) получим:
и т. д. из (1) получим: 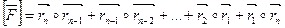 по свойству 2° все слагаемые поменяли знак, а абсолютная величина не изменилась из Ch 3 получаем ч.т.д.
по свойству 2° все слагаемые поменяли знак, а абсолютная величина не изменилась из Ch 3 получаем ч.т.д.
Date: 2015-09-24; view: 530; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |