
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задание № 4
Исследуется зависимость месячного расхода семьи на продукты питания zi, (тыс.р.) от месячного дохода на одного человека семьи хi, (тыс.р.) и от размера семьи уi, (чел.) Необходимо:
1. В соответствии с методом наименьших квадратов найти уравнение множественной линейной регрессии 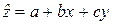 .
.
2. Найти парные коэффициенты корреляции rxy, rxz, ryz.
3. С доверительной вероятностью 0,95 проверить коэффициенты корреляции на значимость.
4. Вычислить индекс множественной корреляции и проверить с доверительной вероятностью 0,95 его статистическую значимость.
| Значения факторов хi и уi (одинаковое для всех вариантов). | |||||||||||||||
| хi | |||||||||||||||
| уi | |||||||||||||||
| Вар. | Значение фактора zi (по вариантам). | ||||||||||||||
| 2,3 | 2,1 | 2,9 | 2,7 | 3,2 | 3,4 | 3,8 | 4,2 | 4,2 | 4,5 | 5,2 | 5,8 | 4,7 | 5,5 | 5,1 |
| хi | уi | Zi |
| 2,3 | ||
| 2,1 | ||
| 2,9 | ||
| 2,7 | ||
| 3,2 | ||
| 3,4 | ||
| 3,8 | ||
| 4,2 | ||
| 4,2 | ||
| 4,5 | ||
| 5,2 | ||
| 5,8 | ||
| 4,7 | ||
| 5,5 | ||
| 5,1 |
РЕШЕНИЕ:
ПЕРЕОБОЗНАЧИМ
Хi=x1
Yi=x2
Zi=y
Уравнение множественной регрессии методом определителей.
Расчет коэффициентов множественной линейной регрессии.
Система трех линейных уравнений с тремя неизвестными b0, b1, b2:
∑yi = nb0 + b1∑x1i + b2∑x2i
∑x1iyi = b0∑x1i + b1∑x1i2 + b2∑x1ix2i
∑x2iyi = b0∑x2i + b1∑x1ix2i + b2∑x2i2
| Y | X1 | X2 | X12 | X22 | X1Y | X2Y | X1X2 | Y2 |
| 2.3 | 4.6 | 2.3 | 5.29 | |||||
| 2.1 | 6.3 | 2.1 | 4.41 | |||||
| 2.9 | 11.6 | 2.9 | 8.41 | |||||
| 2.7 | 5.4 | 5.4 | 7.29 | |||||
| 3.2 | 9.6 | 6.4 | 10.24 | |||||
| 3.4 | 13.6 | 6.8 | 11.56 | |||||
| 3.8 | 11.4 | 11.4 | 14.44 | |||||
| 4.2 | 16.8 | 12.6 | 17.64 | |||||
| 4.2 | 12.6 | 17.64 | ||||||
| 4.5 | 13.5 | 20.25 | ||||||
| 5.2 | 20.8 | 20.8 | 27.04 | |||||
| 5.8 | 23.2 | 33.64 | ||||||
| 4.7 | 9.4 | 23.5 | 22.09 | |||||
| 5.5 | 16.5 | 27.5 | 30.25 | |||||
| 5.1 | 20.4 | 25.5 | 26.01 | |||||
| 59.6 | 209.9 | 256.2 | ||||||
| 3.97 | 3.4 | 12.47 | 13.99 | 13.4 | 10.4 | 17.08 |
Для наших данных система уравнений имеет вид:
59.6 = 15 b0 + 51b1 + 45b2
209.9 = 51b0 + 187b1 + 156b2
201 = 45b0 + 156b1 + 165b2
Решая систему методом Крамера, находим:
b0 = 0.579
b1 = 0.379
b2 = 0.702
Уравнение регрессии:
Y = 0.579 + 0.379 X1 + 0.702 X2
2. Анализ качества эмпирического уравнения множественной линейной регрессии.
Построение эмпирического уравнения регрессии является начальным этапом эконометрического анализа. Первое же построенное по выборке уравнение регрессии очень редко является удовлетворительным по тем или иным характеристикам. Поэтому следующей важнейшей оценкой является проверка качества уравнения регрессии. В эконометрике принята устоявшаяся схема такой проверки, которая проводится по следующим направлениям:
• проверка статистической значимости коэффициентов уравнения регрессии;
• проверка общего качества уравнения регрессии;
• проверка свойств данных, выполнимость которых предполагалась при оценивании уравнения (проверка выполнимости предпосылок МНК).
Прежде чем проводить анализ качества уравнения регрессии, необходимо определить дисперсии и стандартные ошибки коэффициентов, а также интервальные оценки коэффициентов.
При этом:
где m=2 – количество объясняющих переменных модели.
Стандартные ошибки коэффициентов:
| Y(X1,X2) | ei = (Yi-Y(X1,X2)) | ei2 |
| 2.04 | 0.26 | 0.0683 |
| 2.42 | -0.32 | 0.1 |
| 2.8 | 0.1 | 0.0107 |
| 2.74 | -0.0407 | 0.00166 |
| 3.12 | 0.0804 | 0.00646 |
| 3.5 | -0.0986 | 0.00972 |
| 3.82 | -0.0218 | 0.000473 |
| 4.2 | -0.000702 | |
| 4.58 | -0.38 | 0.14 |
| 4.52 | -0.0239 | 0.000569 |
| 4.9 | 0.3 | 0.0883 |
| 5.28 | 0.52 | 0.27 |
| 4.85 | -0.15 | 0.0216 |
| 5.23 | 0.27 | 0.0751 |
| 5.6 | -0.5 | 0.25 |
| 59.6 | -0 | 1.05 |
Оценка мультиколлинеарности факторов.
Парные коэффициенты корреляции.
Для расчета составим следующую таблицу:
| Y | X1 | X2 | (Yi-Yср)2 | (X1i-X1ср)2 | (X2i-X2ср)2 | (Yi-Yср)(X1i-X1ср) | (Yi-Yср)(X2i-X2ср) | (X1i-X1ср)(X2i-X2ср) |
| 2.3 | 2.8 | 1.96 | 2.34 | 3.35 | 2.8 | |||
| 2.1 | 3.51 | 0.16 | 0.75 | 3.75 | 0.8 | |||
| 2.9 | 1.15 | 0.36 | -0.64 | 2.15 | -1.2 | |||
| 2.7 | 1.62 | 1.96 | 1.78 | 1.27 | 1.4 | |||
| 3.2 | 0.6 | 0.16 | 0.31 | 0.77 | 0.4 | |||
| 3.4 | 0.33 | 0.36 | -0.34 | 0.57 | -0.6 | |||
| 3.8 | 0.03 | 0.16 | 0.0693 | |||||
| 4.2 | 0.0514 | 0.36 | 0.14 | |||||
| 4.2 | 0.0514 | 2.56 | 0.36 | |||||
| 4.5 | 0.28 | 0.16 | -0.21 | 0.53 | -0.4 | |||
| 5.2 | 1.5 | 0.36 | 0.74 | 1.23 | 0.6 | |||
| 5.8 | 3.34 | 2.56 | 2.92 | 1.83 | 1.6 | |||
| 4.7 | 0.53 | 1.96 | -1.02 | 1.45 | -2.8 | |||
| 5.5 | 2.33 | 0.16 | -0.61 | 3.05 | -0.8 | |||
| 5.1 | 1.27 | 0.36 | 0.68 | 2.25 | 1.2 | |||
| 59.6 | 19.39 | 13.6 | 7.26 | 22.2 | ||||
| 3.97 | 3.4 | 1.29 | 0.91 | 0.48 | 1.48 | 0.2 |
Для y и x1
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент корреляции
Для y и x2
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент корреляции
Для x1 и x2
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент корреляции
Матрица парных коэффициентов корреляции.
| - | y | x1 | x2 |
| y | 0.447 | 0.92 | |
| x1 | 0.447 | 0.149 | |
| x2 | 0.92 | 0.149 |
Коэффициенты регрессии bi можно также найти по следующим формулам:
где
ryx1, ryx2, rx1x2 - коэффициенты парной корреляции между результатом и каждым из факторов и между факторами; s(x1), s(x2) - среднее квадратическое отклонение 1-го и 2-го факторов соответственно; s(y) - среднее квадратическое отклонение результативного признака.
Параметр a можно определить по формуле:
При оценке мультиколлинеарности факторов следует учитывать, что чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии.
Для отбора наиболее значимых факторов xi учитываются следующие условия:
- связь между результативным признаком и факторным должна быть выше межфакторной связи;
- связь между факторами должна быть не более 0.7;
- при высокой межфакторной связи признака отбираются факторы с меньшим коэффициентом корреляции между ними;
Более объективную характеристику тесноты связи дают частные коэффициенты корреляции, измеряющие влияние на результат фактора xi при неизменном уровне других факторов.
Частные коэффициенты корреляции.
Коэффициент частной корреляции отличается от простого коэффициента линейной парной корреляции тем, что он измеряет парную корреляцию соответствующих признаков (y и xi) при условии, что влияние на них остальных факторов (xj) устранено.
На основании частных коэффициентов можно сделать вывод об обоснованности включения переменных в регрессионную модель. Если значение коэффициента мало или он незначим, то это означает, что связь между данным фактором и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели.
Модель регрессии в стандартном масштабе.
Модель регрессии в стандартном масштабе предполагает, что все значения исследуемых признаков переводятся в стандарты (стандартизованные значения) по формулам:
где хji - значение переменной хji в i-ом наблюдении.
Таким образом, начало отсчета каждой стандартизованной переменной совмещается с ее средним значением, а в качестве единицы изменения принимается ее среднее квадратическое отклонение S.
Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением:
ty = ∑βjtxj
Для оценки β-коэффциентов применим МНК. При этом система нормальных уравнений будет иметь вид:
rx1y=β1+rx1x2•β2 +... + rx1xm•βm
rx2y=rx2x1•β1 + β2 +... + rx2xm•βm
...
rxmy=rxmx1•β1 + rxmx2•β2 +... + βm
Для наших данных (берем из матрицы парных коэффициентов корреляции):
0.447 = β1 + 0.149β2
0.92 = 0.149β1 + β2
Данную систему линейных уравнений решаем методом Гаусса: β1 = 0.317; β2 = 0.873;
Искомое уравнение в стандартизованном масштабе: ty=β1tx1+β2tx2
Расчет β-коэффициентов можно выполнить и по формулам:
Стандартизированная форма уравнения регрессии имеет вид:
y0 = 0.317x1 + 0.873x2
Найденные из данной системы β–коэффициенты позволяют определить значения коэффициентов в регрессии в естественном масштабе по формулам:
Вычисляем стандартные коэффициенты регрессии через коэффициенты множественной регрессии b1 и b2:
Получаем уравнение регрессии в стандартизированном масштабе:
y = 0.317tx1 + 0.873tx2
4. Оценка тесноты связи.
4. Теснота связи результативного признака с факторными определятся величиной коэффициента линейной множественной корреляции и детерминации, который могут быть исчислены на основе матрицы парных коэффициентов корреляции:
Более объективную оценку качества построенной модели дает скорректированный индекс множественной детерминации, учитывающий поправку на число степеней свободы:
где n - число наблюдений, m – число факторов.
Сравнительная оценка влияния анализируемых факторов на результативный признак.
5. Сравнительная оценка влияния анализируемых факторов на результативный признак производится:
- средним коэффициентом эластичности, показывающим на сколько процентов среднем по совокупности изменится результат y от своей средней величины при изменении фактора xi на 1% от своего среднего значения;
Частный коэффициент эластичности E1 < 1. Следовательно, его влияние на результативный признак Y незначительно.
Частный коэффициент эластичности E2 < 1. Следовательно, его влияние на результативный признак Y незначительно.
- β–коэффициенты, показывающие, что, если величина фактора изменится на одно среднеквадратическое отклонение Sxi, то значение результативного признака изменится в среднем на β своего среднеквадратического отклонения;
- долю каждого фактора в общей вариации результативного признака определяют коэффициенты раздельной детерминации (отдельного определения): d2i = ryxiβi.
d21 = 0.45 • 0.317 = 0.14.
d22 = 0.92 • 0.873 = 0.8.
При этом должно выполняться равенство:
d21 + d22 = R2yx1x2.
6. Оценка значимости коэффициентов регрессии с помощью t-критерия Стьюдента.
Оценка значимости коэффициентов регрессии b1 и b2 производится с помощью t-критерия Стьюдента и связана с сопоставлением их значений с величиной случайных ошибок mb1 и mb2. Более простым способом расчета фактических значений tb1 и tb2 является их определение через критерии F:
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=.
tкрит (n-m-1;α/2) = (12;0) = 12
Поскольку 1.87 < 12, то статистическая значимость коэффициента регрессии b0 не подтверждается (принимаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 4.67 < 12, то статистическая значимость коэффициента регрессии b1 не подтверждается (принимаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 12.85 > 12, то статистическая значимость коэффициента регрессии b2 подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 100% будут следующими:
(bj - tкрит Sbj; bj + tкрит Sbj)
(0.58 - 12 • 0.31; 0.58 + 12 • 0.31)
(-3.13;4.29)
С вероятностью 100% можно утверждать, что значение данного параметра b0 будут лежать в найденном интервале.
(0.38 - 12 • 0.0812; 0.38 + 12 • 0.0812)
(-0.6;1.35)
С вероятностью 100% можно утверждать, что значение данного параметра b1 будут лежать в найденном интервале.
(0.7 - 12 • 0.0546; 0.7 + 12 • 0.0546)
(0.0463;1.36)
С вероятностью 100% можно утверждать, что значение данного параметра b2 будут лежать в найденном интервале.
7. Проверка гипотезы о статистической значимости уравнения регрессии.
Проверка гипотезы H0 о статистической значимости уравнения регрессии и показателя тесноты связи (R2 = 0) производится по F-критерию Фишера сравнением Fфакт с Fтабл.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=2 для множественной регрессии с двумя факторами.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 2 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2-1.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=2 и k2=12, Fkp = 3.89
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).
Частные критерии.
Частные критерии Fx1 и Fx2 оценивают статистическую значимость включения факторов x1 и x2 в уравнение множественной регрессии и целесообразность включения в уравнение одного фактора после другого, т.е. Fx1 оценивает целесообразность включения в уравнение x1 после включения в него фактора x2.
Соответственно Fx2 указывает на целесообразность включения в модель фактора x2 после включения фактора x1.
Поскольку фактическое значение F > Fkp, то коэффициент Fx1 статистически значим, т.е. целесообразно включать в уравнение x1 после включения в него фактора x2.
Поскольку фактическое значение F > Fkp, то коэффициент Fx2 статистически значим, т.е. целесообразно включать в уравнение x2 после включения в него фактора x1.
Date: 2015-09-22; view: 646; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |